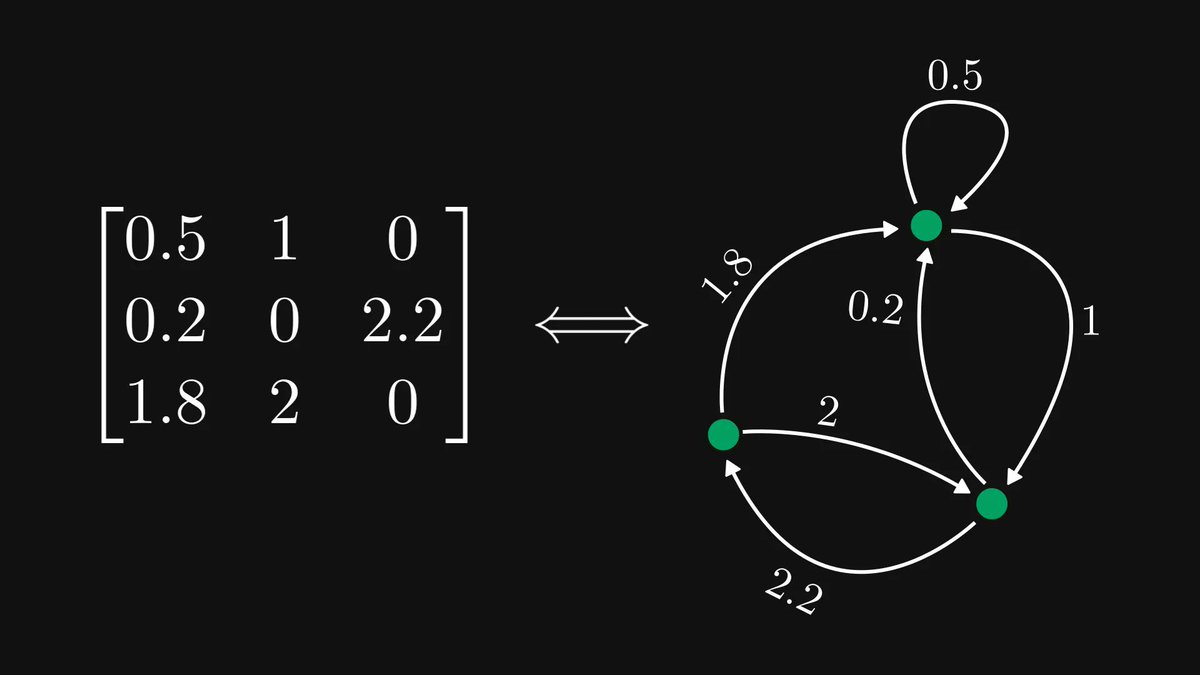
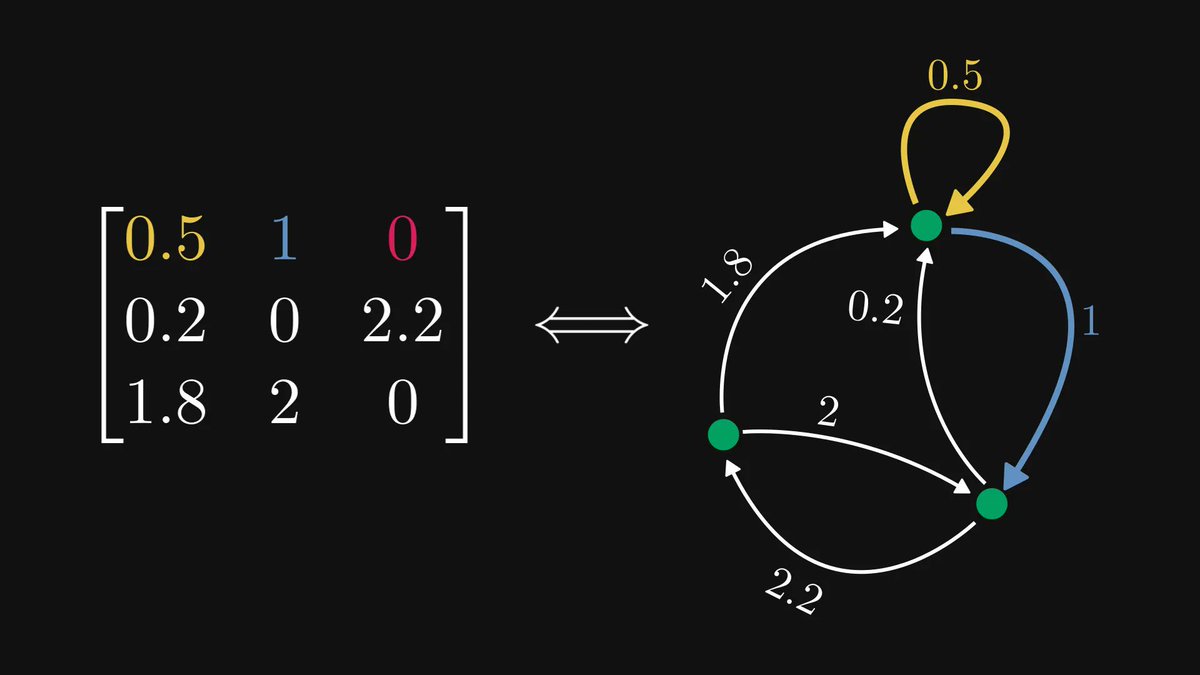
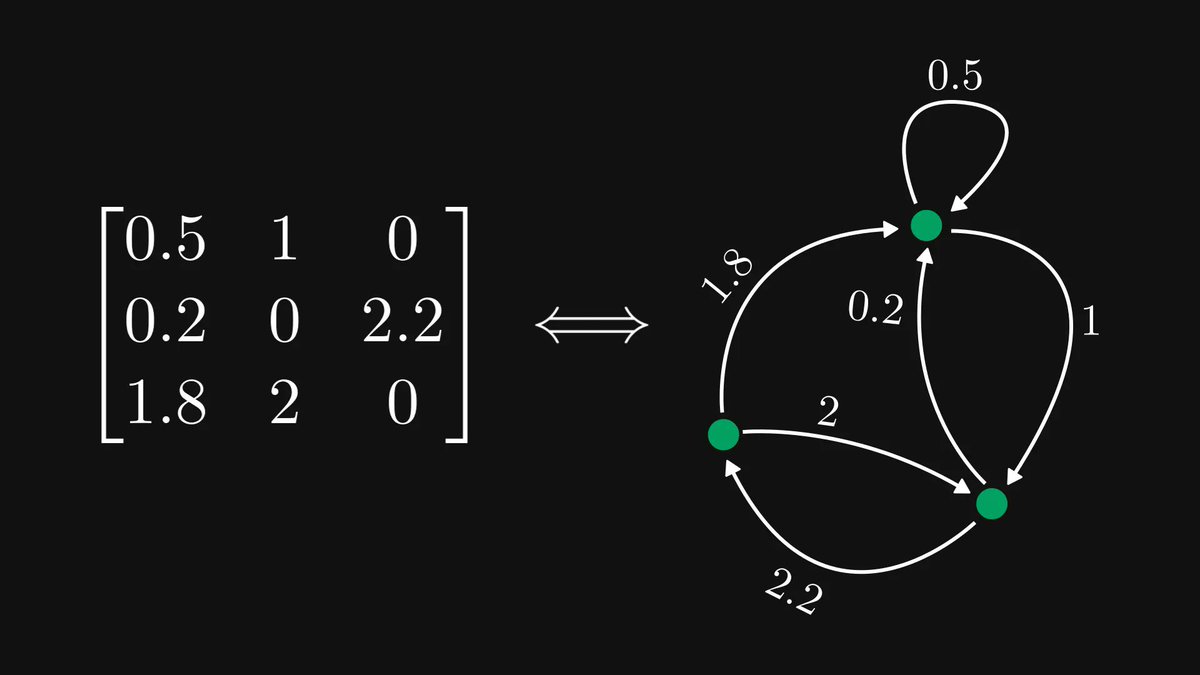
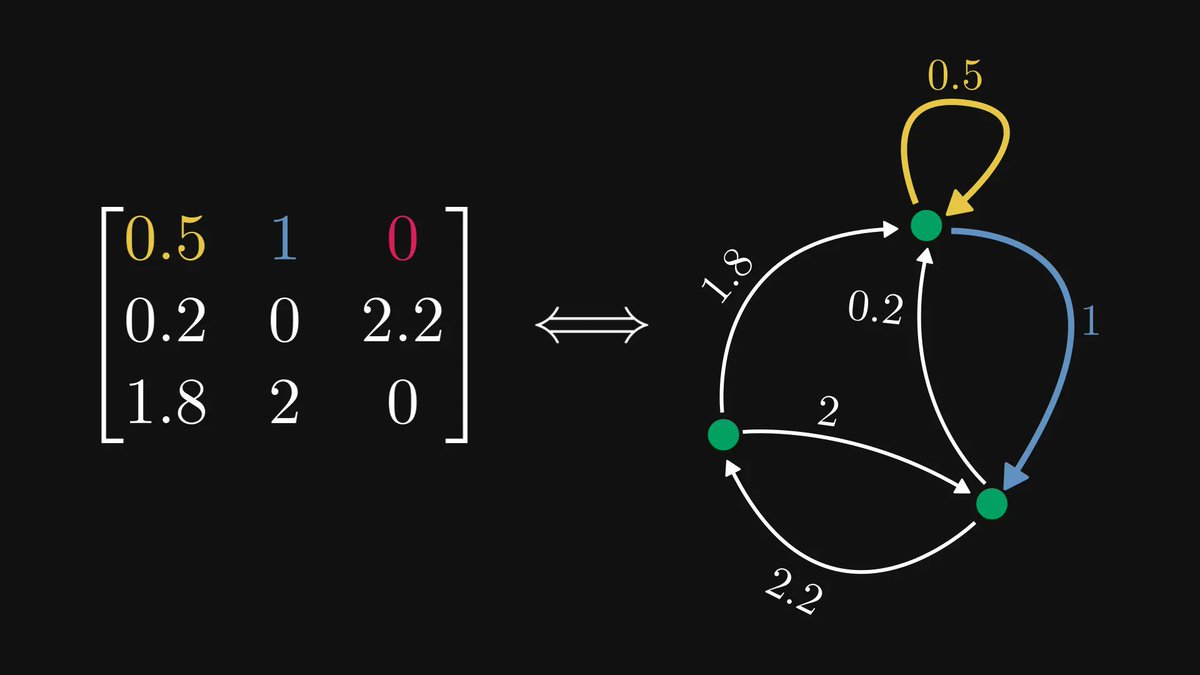
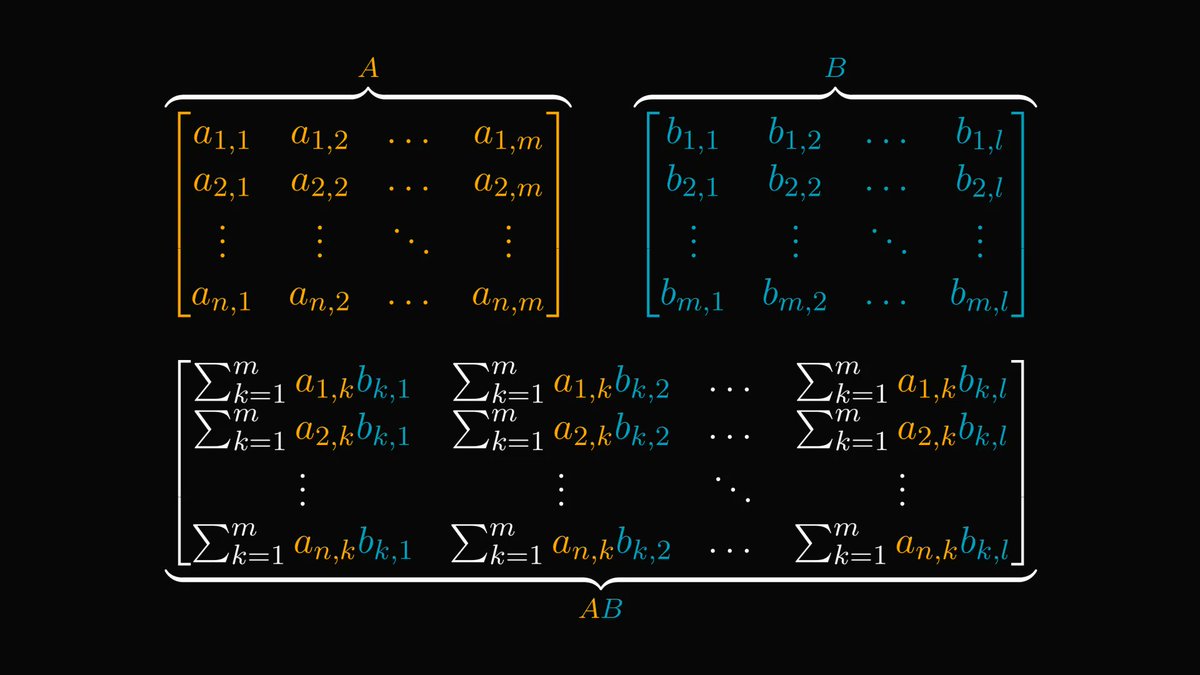
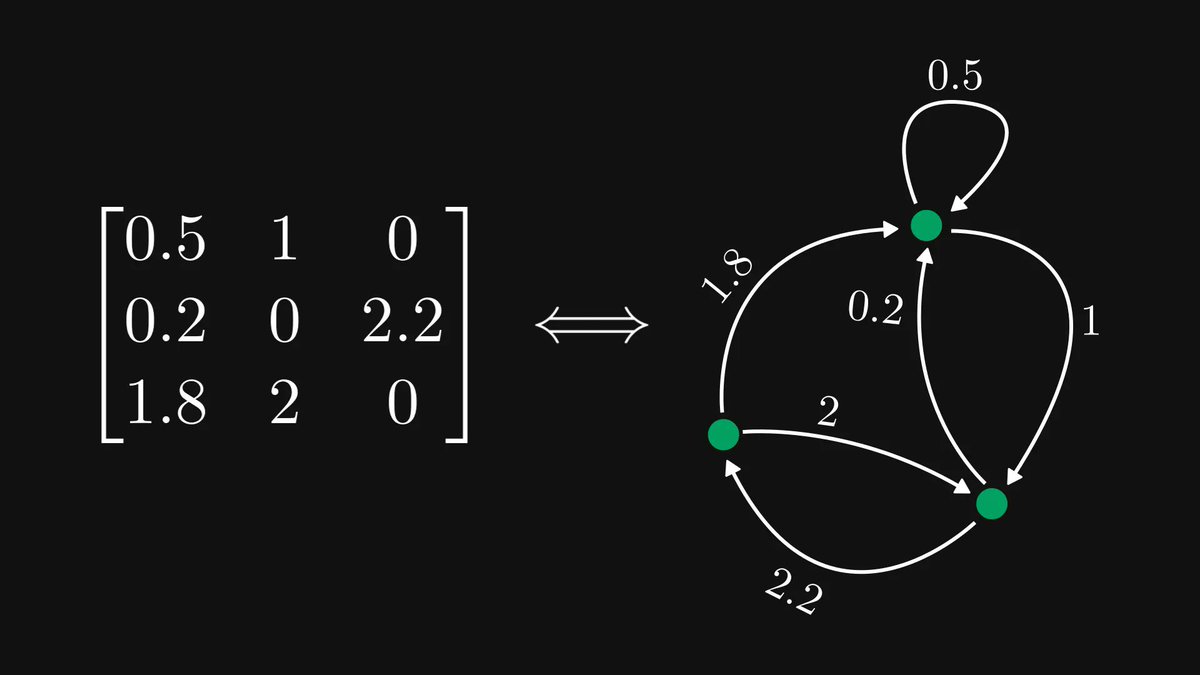
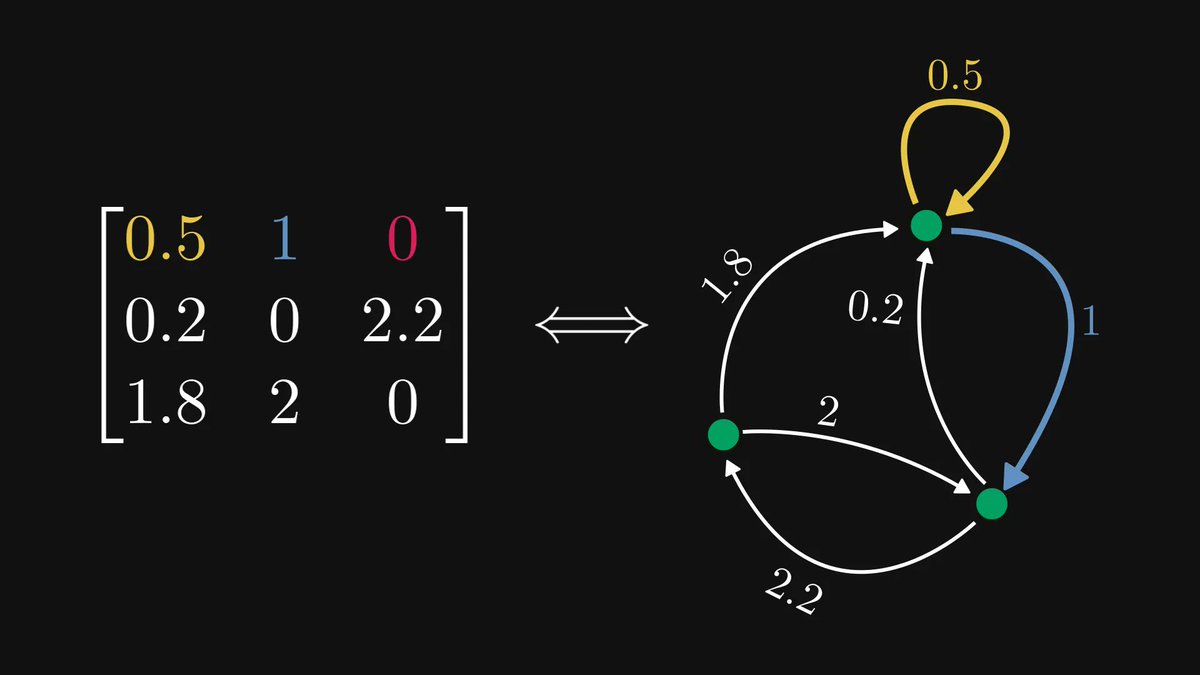
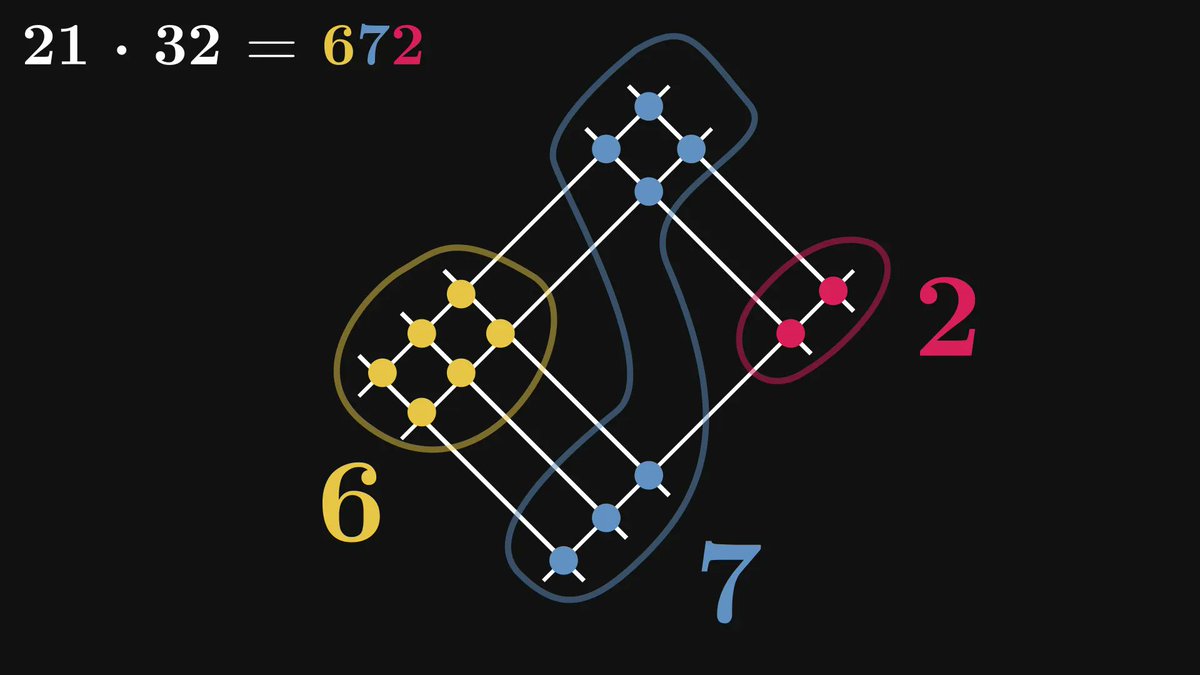
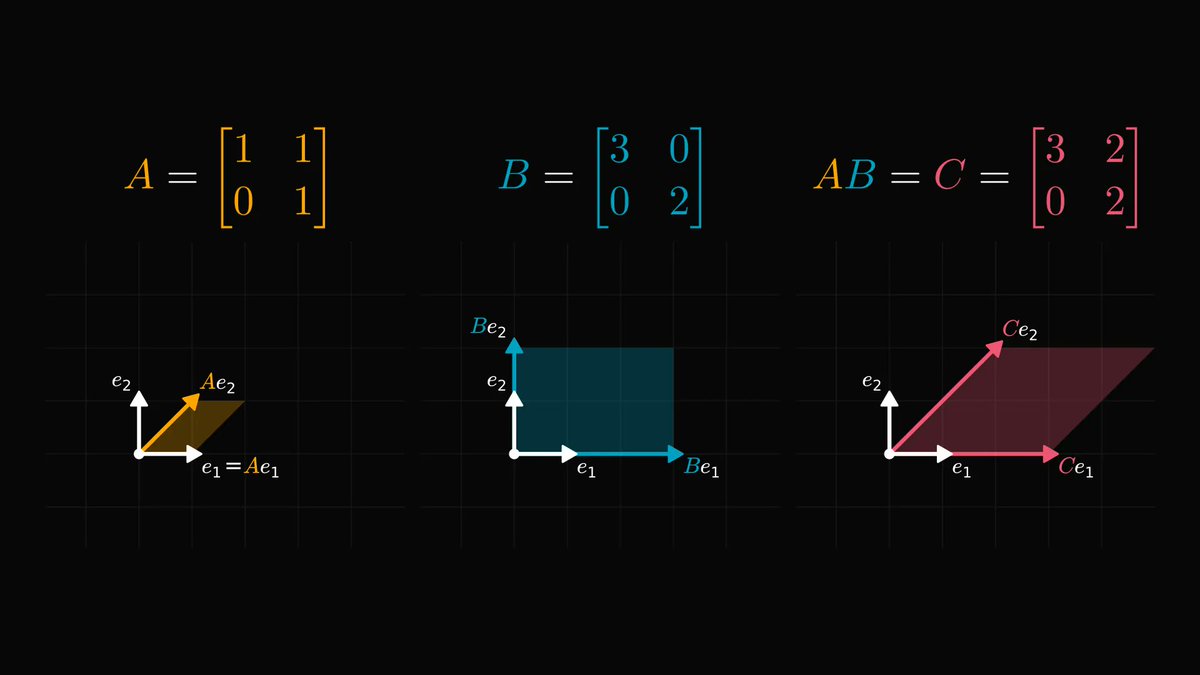I described some of the most beautiful and famous mathematical theorems to Midjourney.
Here is how it imagined them:
1. "The set of real numbers is uncountably infinite."
Here is how it imagined them:
1. "The set of real numbers is uncountably infinite."
2. The Baire category theorem: "In a complete metric space, the intersection of countably many dense sets remains dense."
3. Zorn's lemma: "A partially ordered set containing upper bounds for every chain necessarily contains at least one maximal element."
4. The fundamental theorem of calculus: "The integral of a function's derivative recovers the original function, up to a constant."
5. The Banach-Tarski paradox: "Decomposing a solid sphere into a finite number of disjoint subsets, and then reassembling those subsets to create two spheres identical to the original one."
6. "Every vector space has a Hamel basis."
7. The fundamental theorem of algebra: "Every non - constant polynomial equation has at least one complex root."
8. Gödel's incompleteness theorems: "In any formal system of axioms, there are true statements that cannot be proven within the system and the consistency of the system cannot be proven by its own axioms."
9. The fundamental theorem of arithmetic: "Every positive integer greater than 1 can be represented uniquely as a product of prime numbers."
10. Brouwer's fixed point theorem: "In any continuous transformation of a compact, convex set in Euclidean space, there is at least one point that remains fixed."
11. The central limit theorem: "The sum of a large number of independent and identically distributed random variables will be approximately normally distributed, regardless of the original distribution."
12. The Heine-Borel theorem: "The compact subsets of Euclidean space are precisely those that are closed and bounded."
13. The singular value decomposition: "Every matrix can be decomposed into the product of a unitary, a diagonal, and another unitary matrix."
14. Bonus: "The set of real numbers is uncountably infinite, in the style of Salvador Dali."
If you have enjoyed this thread, share it with your friends and give me a follow!
This is not my typical content: I usually post math explainers here. However, this was my first time trying out Midjourney. Now, I am hooked.
(Don't worry, I won't go into "AI influencer" mode.)
This is not my typical content: I usually post math explainers here. However, this was my first time trying out Midjourney. Now, I am hooked.
(Don't worry, I won't go into "AI influencer" mode.)
https://twitter.com/TivadarDanka/status/1649721970886594561
• • •
Missing some Tweet in this thread? You can try to
force a refresh
