Read on Twitter
๐น If ML model is not accurate. it can make predictions error & these prediction errors are usually known as Bias & Variance
๐น In ML these errors will alway be present as there is always slight difference between model predictions & actual predictions
๐น In ML these errors will alway be present as there is always slight difference between model predictions & actual predictions
๐นThe main aim of ML/data science analysts is to reduce these errors in order to get more accurate result
๐นIn ML an error is measure of how accurately an algorithm can make predictions for the previously unknown dataset
๐นIn ML an error is measure of how accurately an algorithm can make predictions for the previously unknown dataset
1โฃ Bias :
While making prediction difference occur between prediction values made by model & actual values/expected values & this difference is known as bias errors or Error due to bias
While making prediction difference occur between prediction values made by model & actual values/expected values & this difference is known as bias errors or Error due to bias
๐นIt can be defined as an inability of ML algorithms such as Linear Regression to capture true relationship between data points
๐นEach algorithm begins with some amount of bias because bias occurs from assumptions in the model, which makes the target function simple to learn
๐นEach algorithm begins with some amount of bias because bias occurs from assumptions in the model, which makes the target function simple to learn
๐นA high bias model also cannot perform well on new data
๐นA low bias model will make fewer assumptions about the form of the target function.
๐นA low bias model will make fewer assumptions about the form of the target function.
๐นThe simpler the algorithm, the higher the bias
๐น Whereas a nonlinear algorithm often has low bias
๐น Whereas a nonlinear algorithm often has low bias
2โฃ Variance
๐นvariance tells that how much a random variable is different from its expected value
๐นvariance tells that how much a random variable is different from its expected value
Low variance : means there is a small variation in the prediction of the target function with changes in the training data set. At the same time
High variance : shows a large variation in the prediction of the target function with changes in the training dataset
High variance : shows a large variation in the prediction of the target function with changes in the training dataset
Bias-Variance Trade-Off
So, it is required to make a balance between bias and variance errors, and this balance between the bias error and variance error is known as the Bias-Variance trade-off
So, it is required to make a balance between bias and variance errors, and this balance between the bias error and variance error is known as the Bias-Variance trade-off
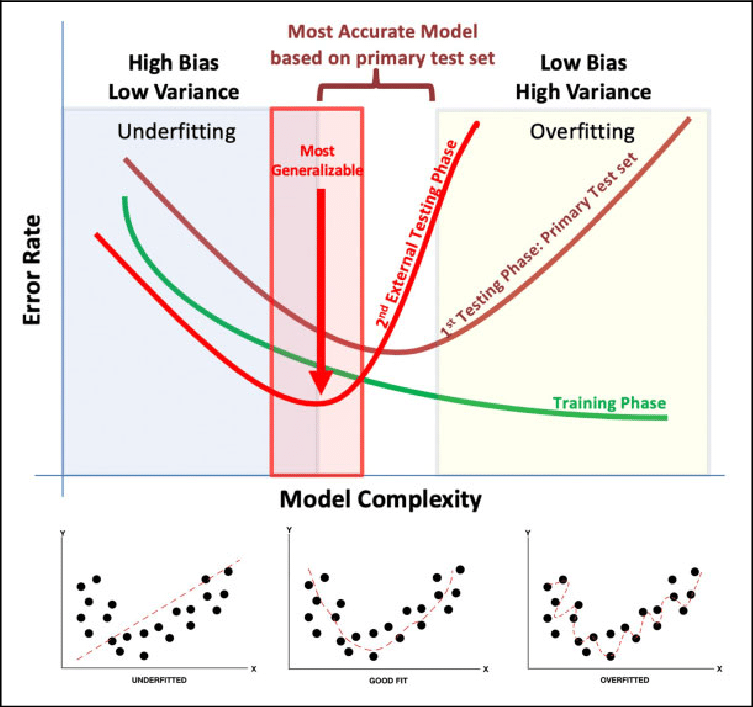
Bias-Variance trade-off is a central issue in supervised learning. Ideally, we need a model that accurately captures the regularities in training data and simultaneously generalizes well with the unseen dataset @pagejavatpoint
javatpoint.com/bias-and-variaโฆ
javatpoint.com/bias-and-variaโฆ
๐นIf this thread was helpful to you
1. Follow me @Sachintukumar
for daily content
2. Connect with me on Linkedin: linkedin.com/in/sachintukumโฆ
3. RT tweet below to share it with your friend
1. Follow me @Sachintukumar
for daily content
2. Connect with me on Linkedin: linkedin.com/in/sachintukumโฆ
3. RT tweet below to share it with your friend
โข โข โข
Missing some Tweet in this thread? You can try to
force a refresh
ใ
