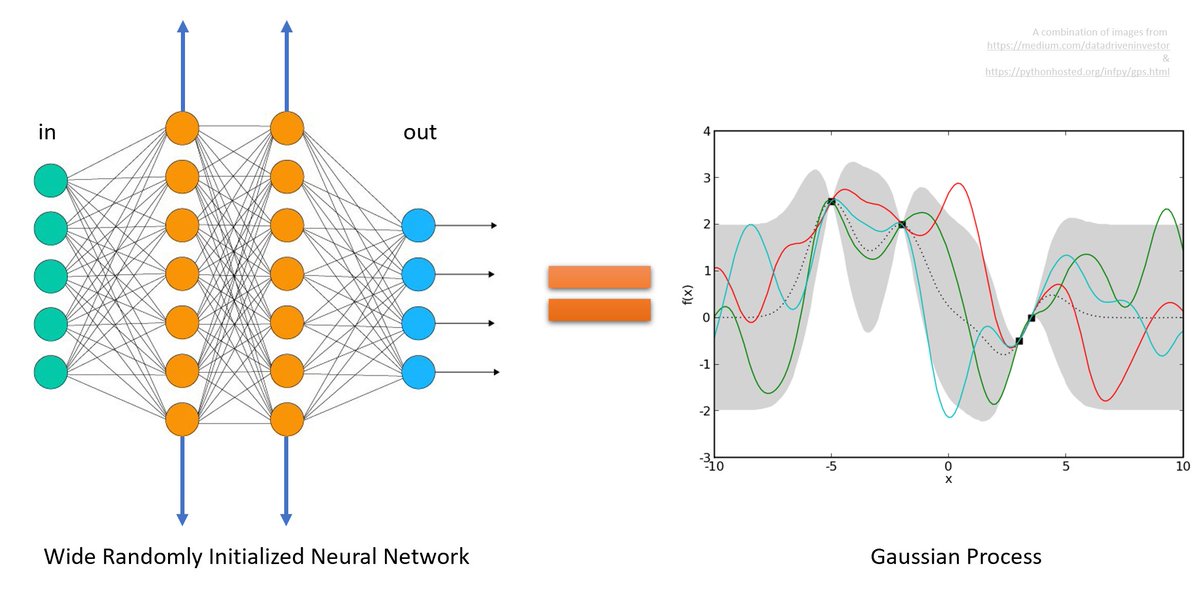
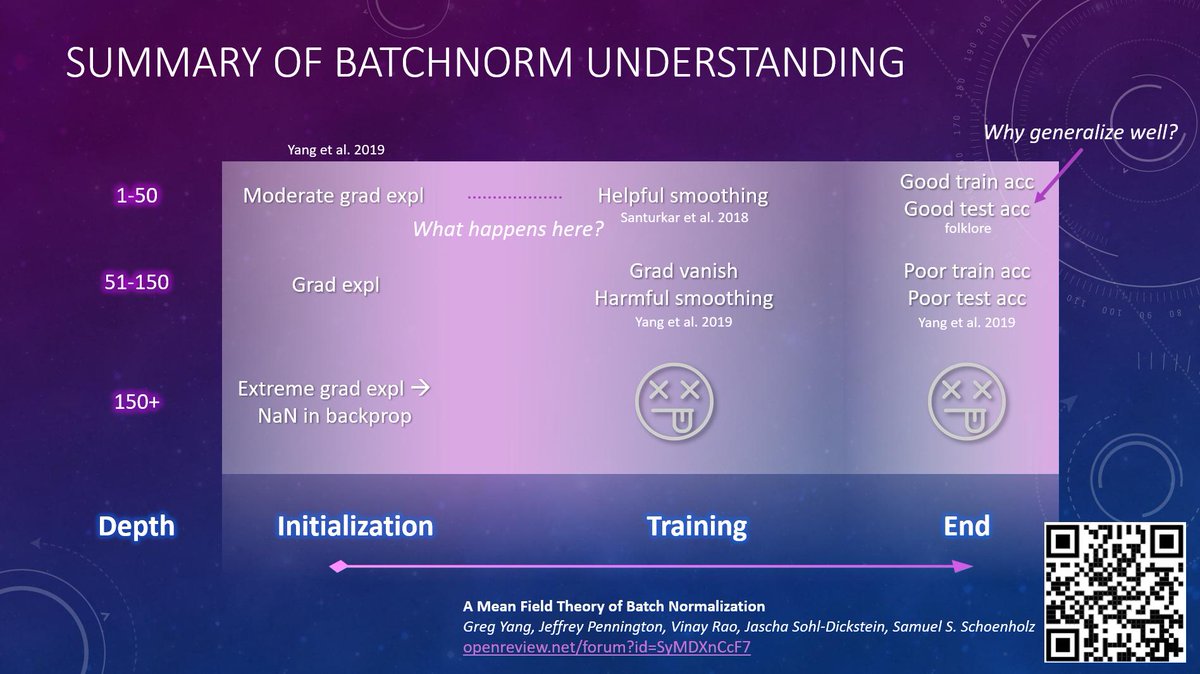
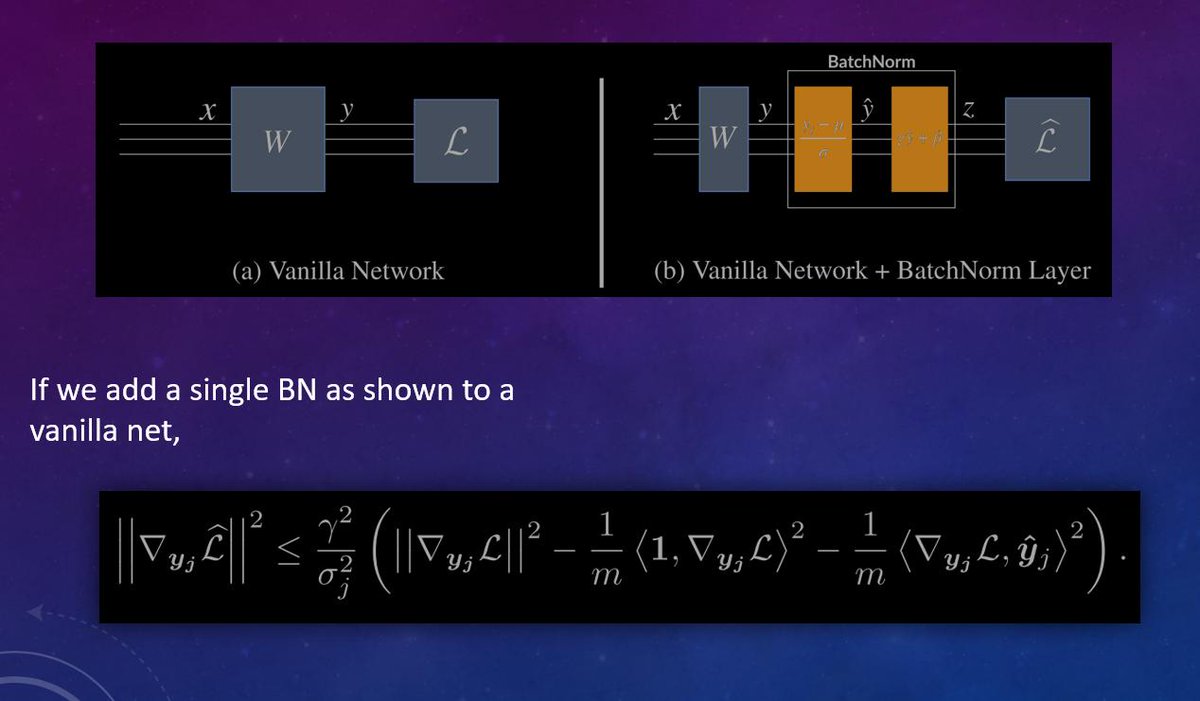
Since folks are asking:
The books I mentioned on @xai spaces are "Linear Algebra Done Right" by Axler and "Naive Set Theory" by Halmos. Other math books that I really enjoyed over the years:
"Introduction to Algorithms" by Thomas H. Cormen & Charles E. Leiserson & Ronald L.… twitter.com/i/web/status/1…
The books I mentioned on @xai spaces are "Linear Algebra Done Right" by Axler and "Naive Set Theory" by Halmos. Other math books that I really enjoyed over the years:
"Introduction to Algorithms" by Thomas H. Cormen & Charles E. Leiserson & Ronald L.… twitter.com/i/web/status/1…
I have about 400+ books in my collection from which these come from. I can dump them here if people are really interested.
• • •
Missing some Tweet in this thread? You can try to
force a refresh

 Read on Twitter
Read on Twitter