
How to get URL link on X (Twitter) App



 2/ 📜
2/ 📜 
 2/ The idea is actually really simple: in a special parametrization introduced in arxiv.org/abs/2011.14522 called µP, narrow and wide neural networks share the same set of optimal hyperparameters. This works even as width -> ∞.
2/ The idea is actually really simple: in a special parametrization introduced in arxiv.org/abs/2011.14522 called µP, narrow and wide neural networks share the same set of optimal hyperparameters. This works even as width -> ∞. 
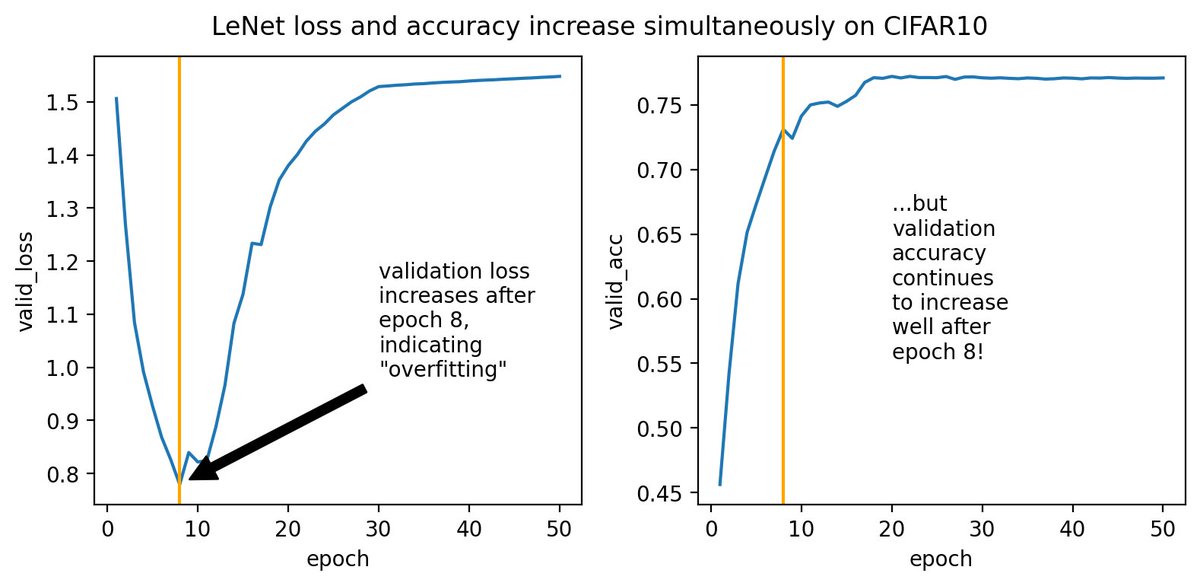
 2/4 More precisely, classic theory goes like this "when we train using xent loss, we get good pop loss by early stopping b4 valid loss 🡅. B/c xent is a good proxy for 0-1 loss, we expect good pop accuracy from this procedure." But here we got good acc w/o getting good pop loss
2/4 More precisely, classic theory goes like this "when we train using xent loss, we get good pop loss by early stopping b4 valid loss 🡅. B/c xent is a good proxy for 0-1 loss, we expect good pop accuracy from this procedure." But here we got good acc w/o getting good pop loss 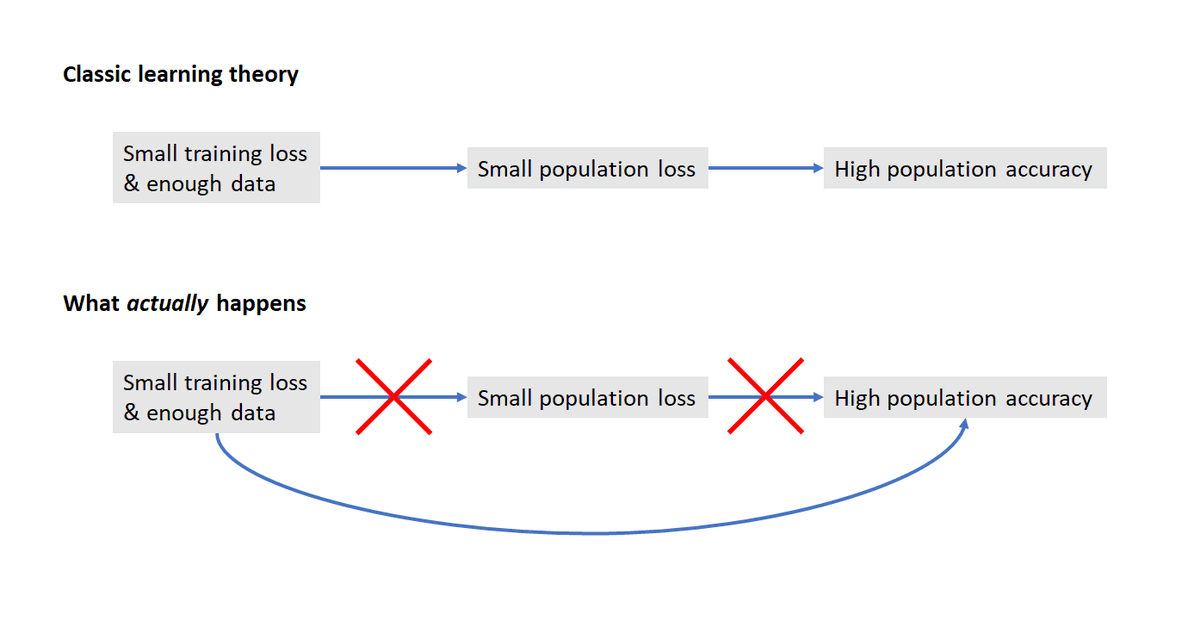
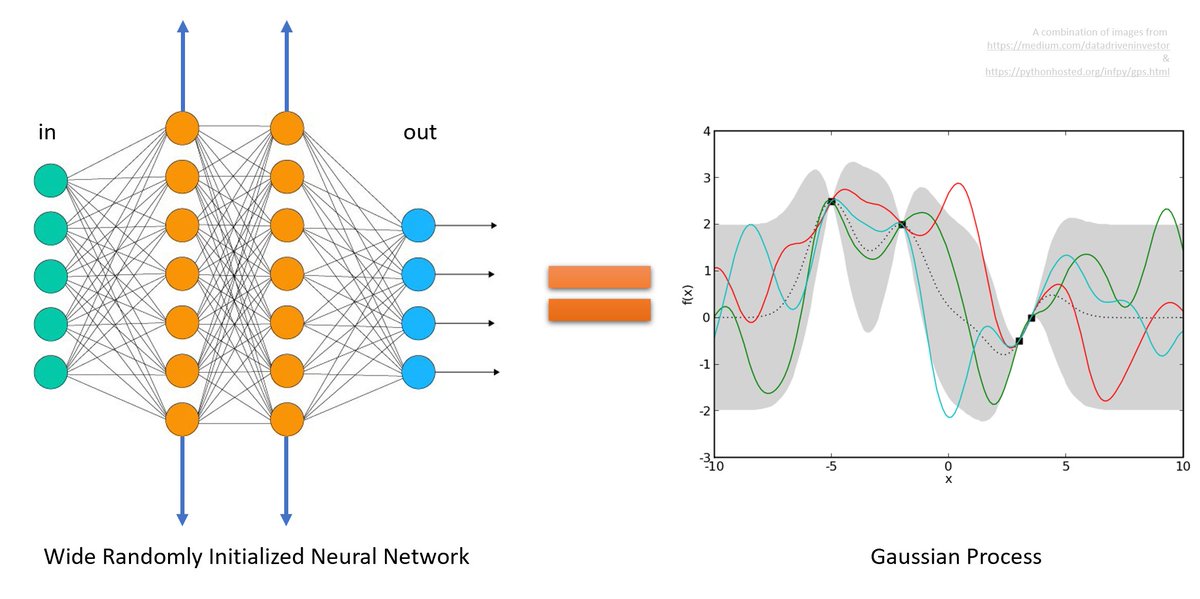
 2/ Part 1 shows that any architecture can be expressed as a principled combination of matrix multiplication and nonlinearity application; such a combination is called a *tensor program*. The image shows an example. Thread 👉
2/ Part 1 shows that any architecture can be expressed as a principled combination of matrix multiplication and nonlinearity application; such a combination is called a *tensor program*. The image shows an example. Thread 👉 
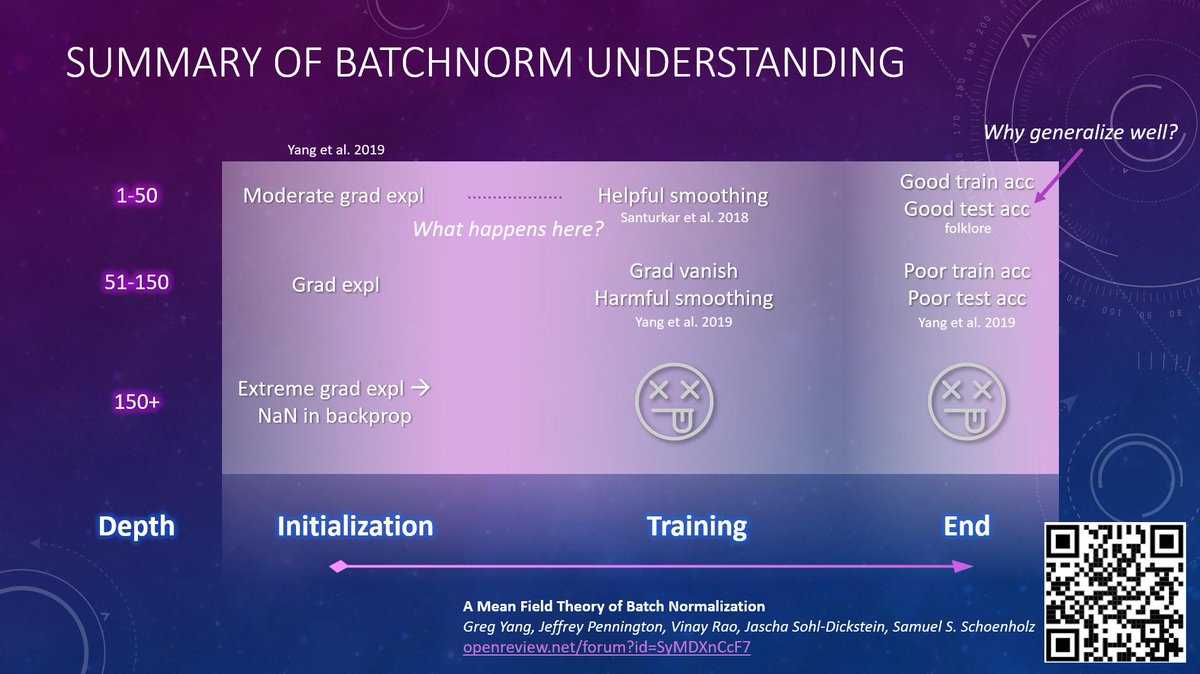
 2/ During a visit by @aleks_madry's students @ShibaniSan @tsiprasd @andrew_ilyas to MSR Redmond few weeks ago, we figured out the apparent paradox.
2/ During a visit by @aleks_madry's students @ShibaniSan @tsiprasd @andrew_ilyas to MSR Redmond few weeks ago, we figured out the apparent paradox.