Thread by @TivadarDanka

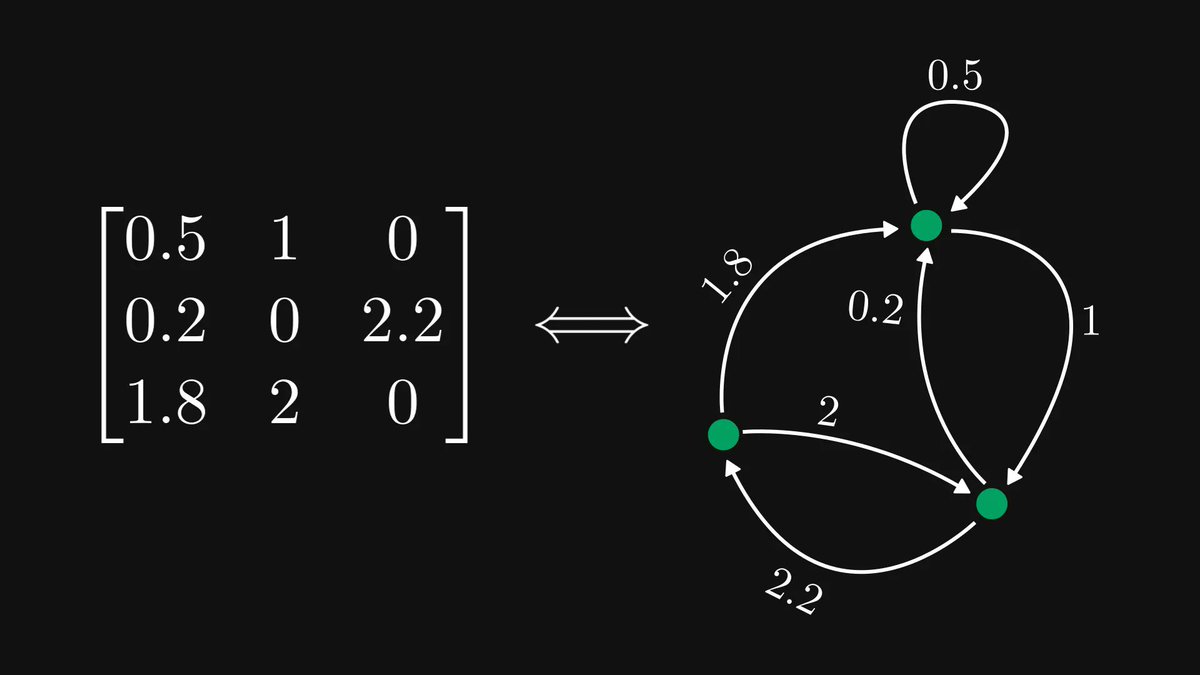
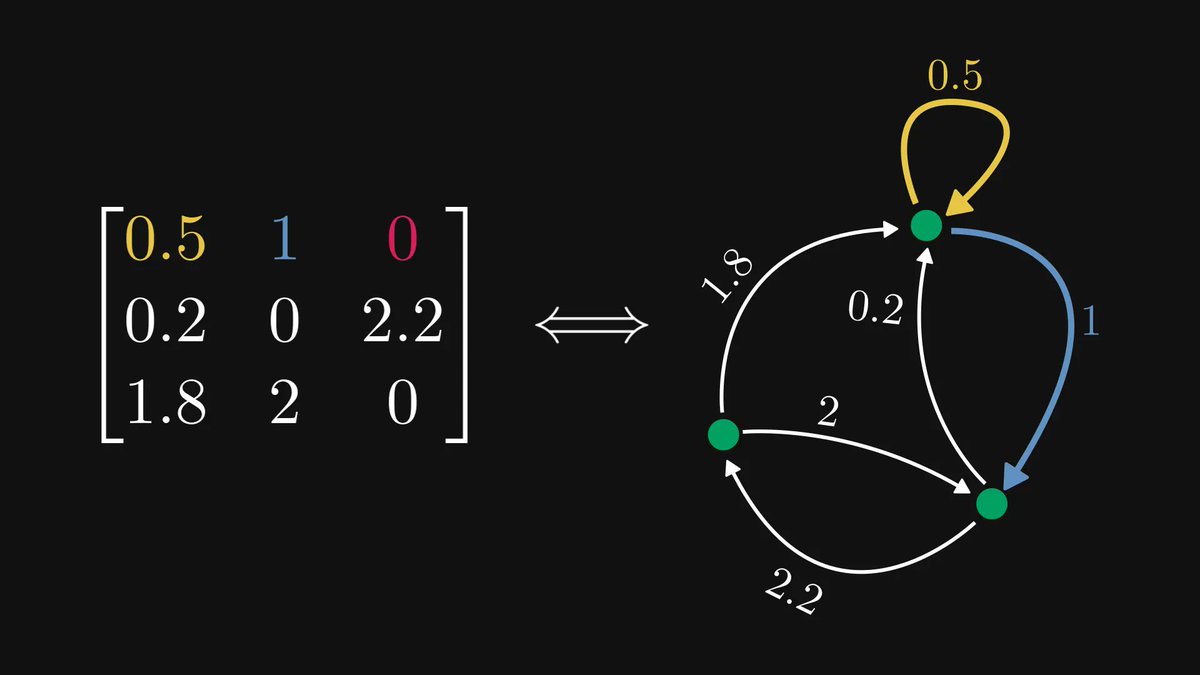
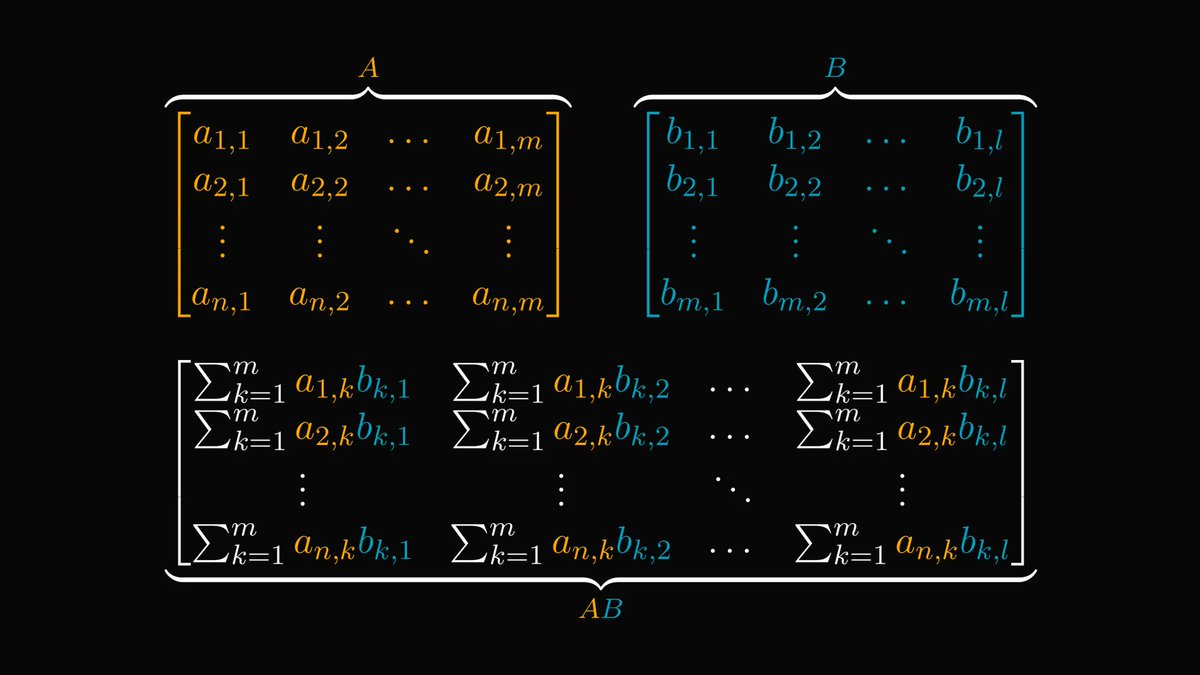
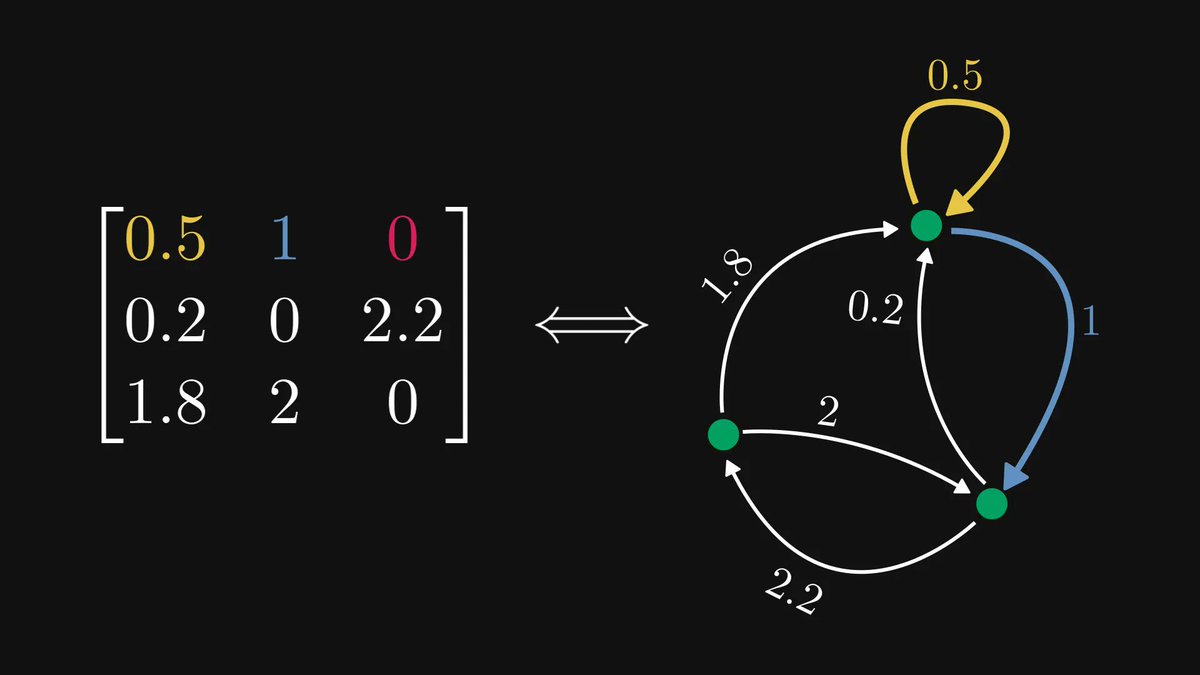
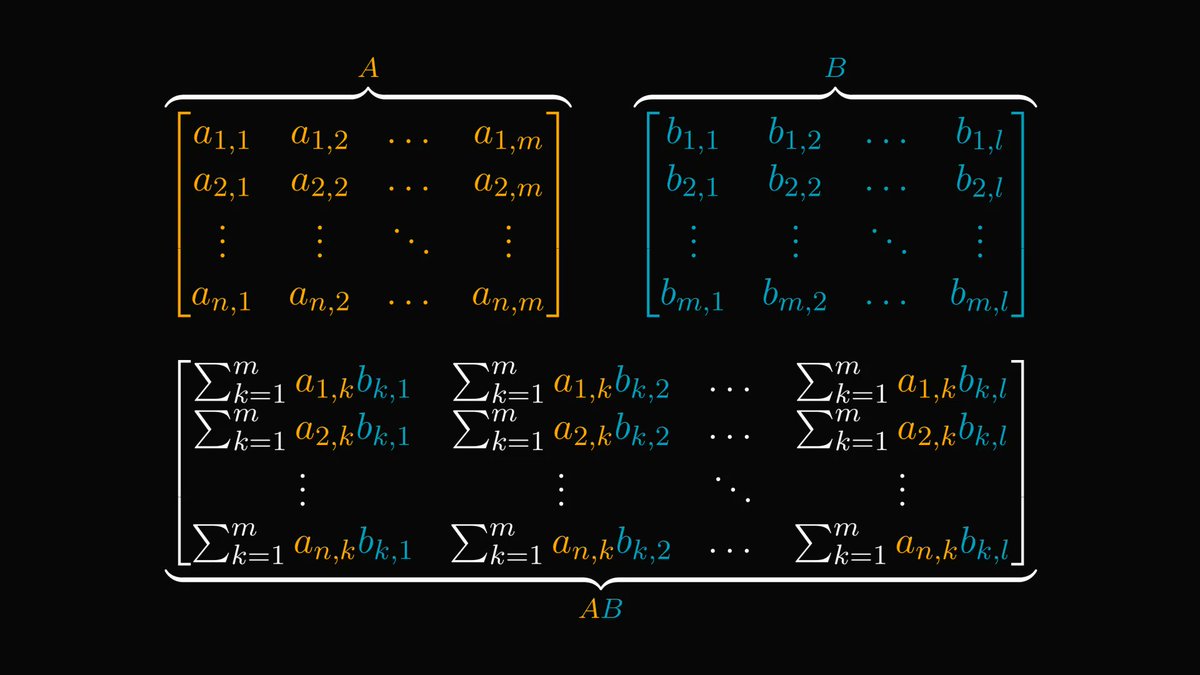
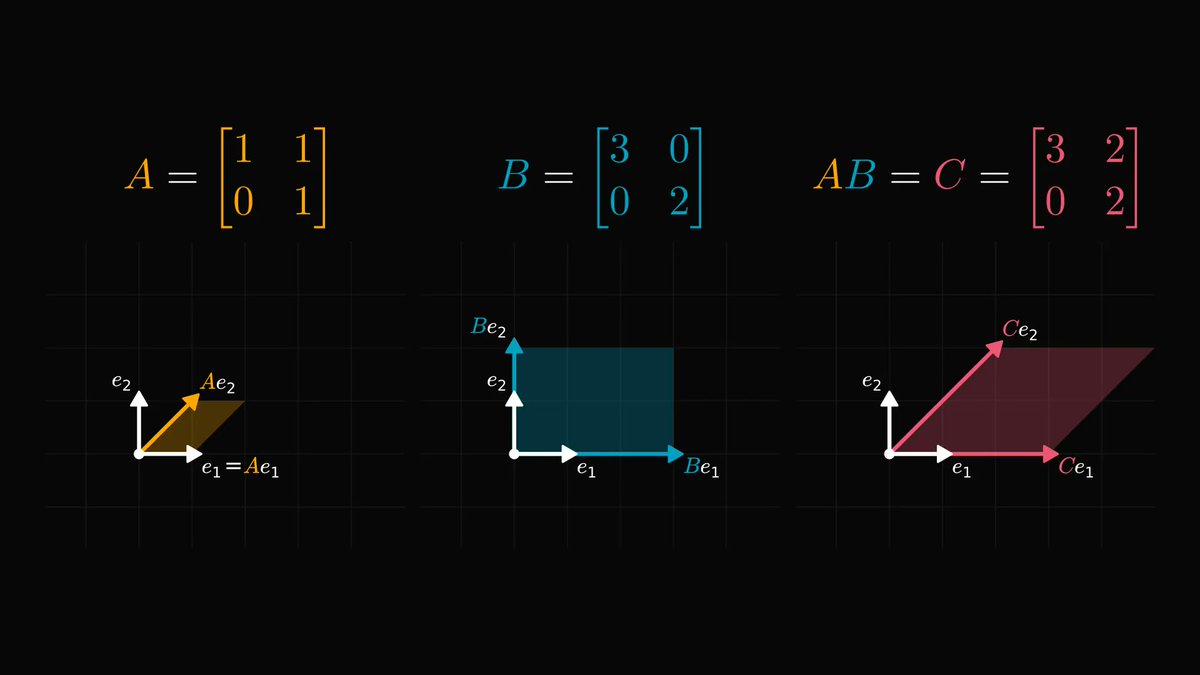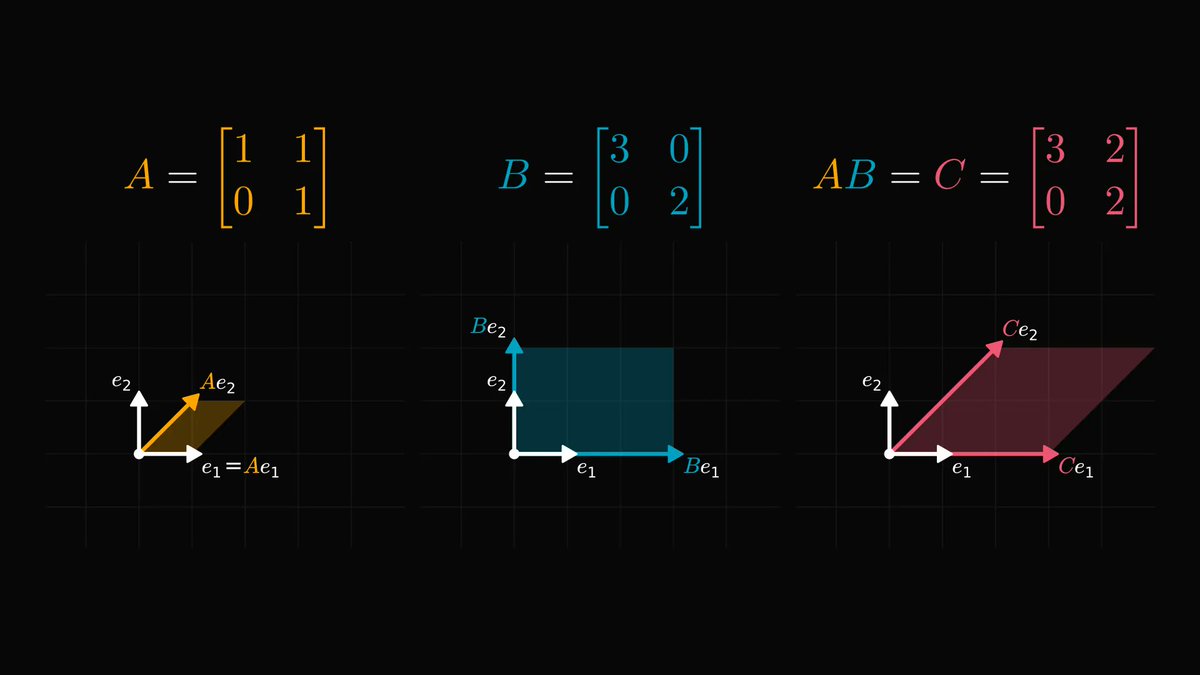Understanding graph theory will seriously enhance your engineering skills; you must absolutely be familiar with them.

Here's a graph theory quickstart, in collaboration with Alejandro Piad Morffis.

Read on:

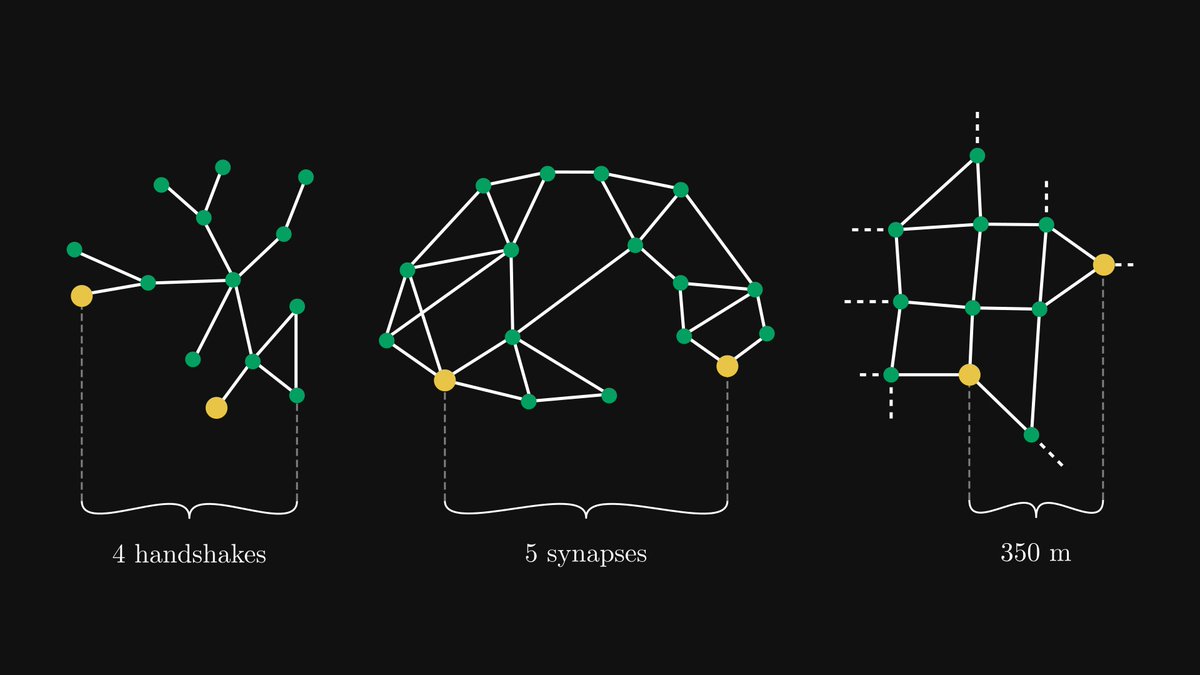
What do the internet, your brain, the entire list of people you’ve ever met, and the city you live in have in common?

These are all radically different concepts, but they share a common trait.

They are all networks that establish relationships between objects.

As distinct as these things seem to be, they share common properties.

For example, the meaning of “distance” is different for

• physical networks,
• information netorks,
• orf social networks,

but in all cases, there is a sense in which some objects are “close” or “far”.

What if we could study this abstract notion of networks of interconnected elements, and understand the fundamental properties of all sorts of networks all at once?

This is the purpose of graph theory, and we’re here to open a window for you to dive into this universe.

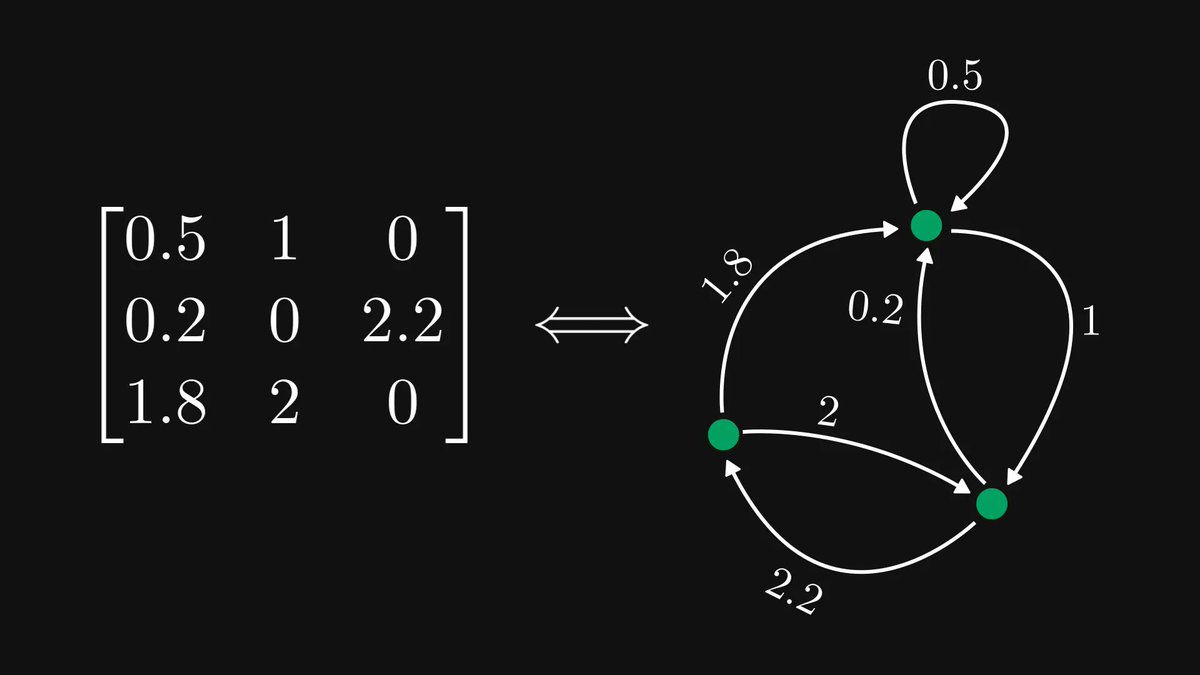
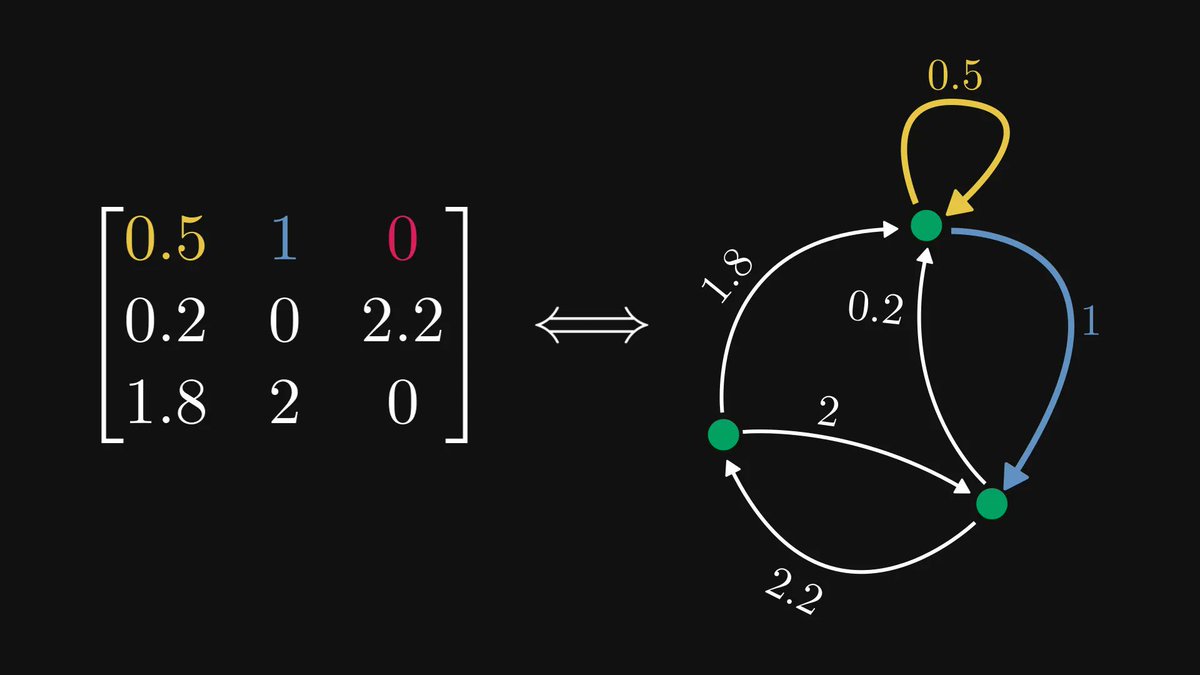
Intuitively, a graph is just a (finite) collection of elements — vertices, or sometimes nodes — connected by edges.

Thus, a graph represents an abstract relation space, in which the edges define who’s related to whom, whatever the nature of that relation is.

There is nothing intrinsic to names or exact locations of the vertices in the drawing.

The layout of a graph is arbitrary, and thus, the same graph can be represented in an infinite number of ways.

In the study of networks, indirect connections are as important as direct ones.

Speaking in the language of graphs, indirect connections are formalized by walks. A walk is simply a finite sequence of connected nodes.

For example, (a, b, a, e, c, d) is a walk on the graph below.

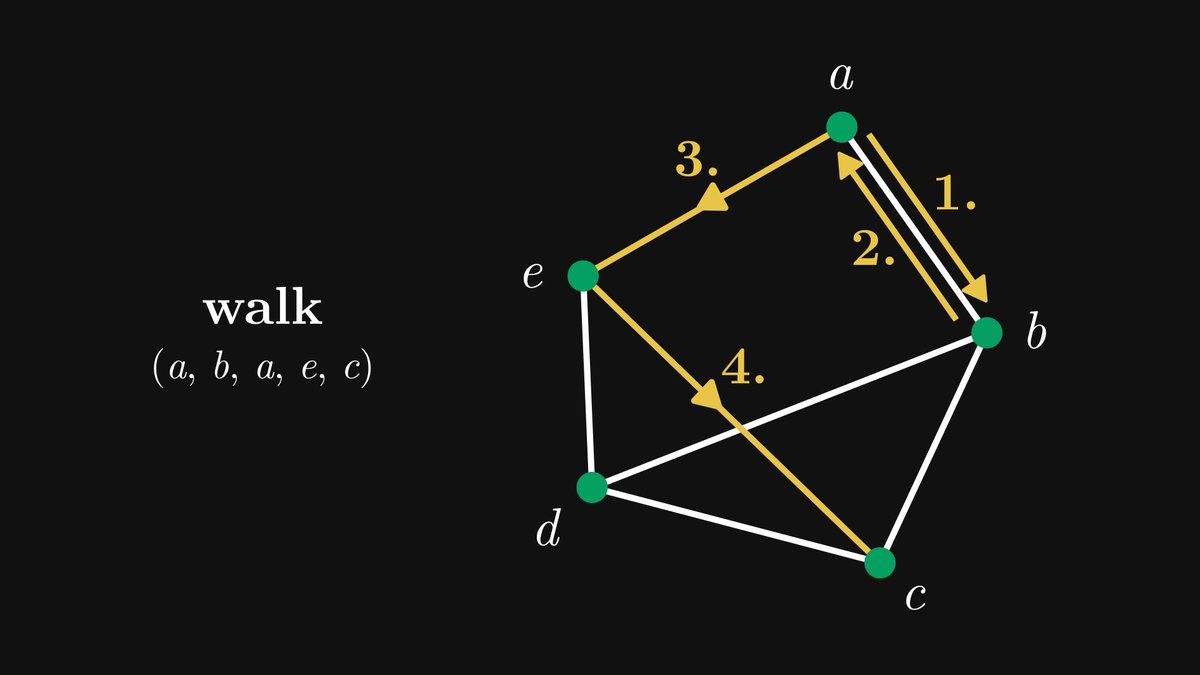
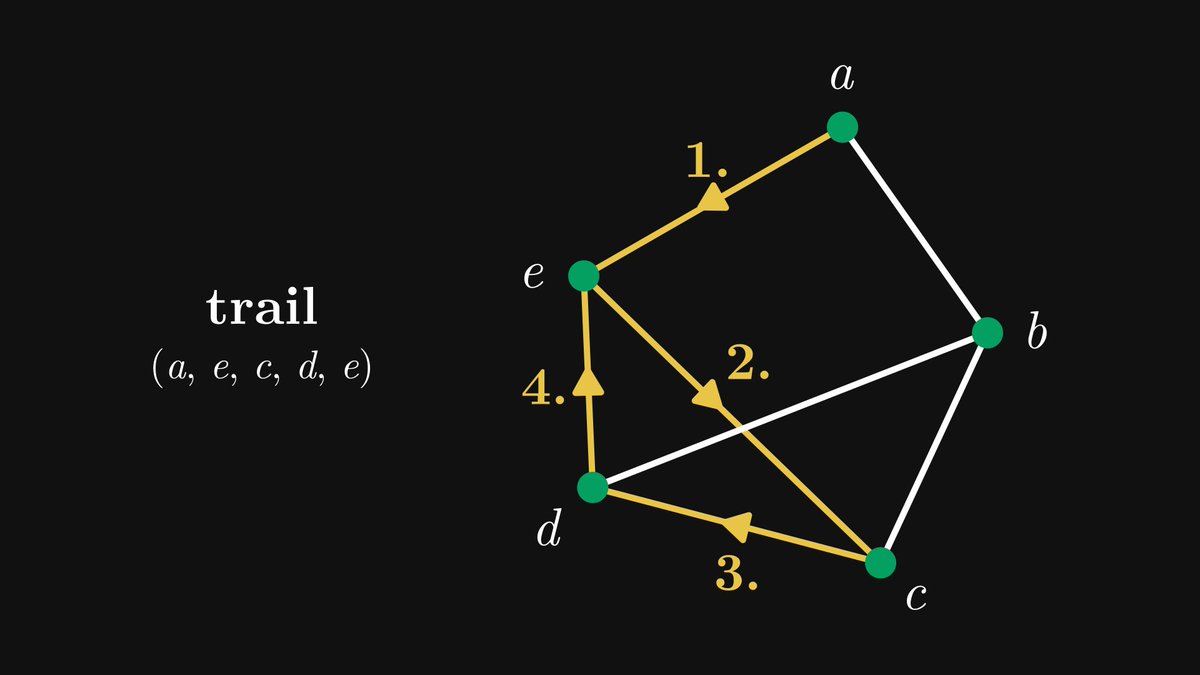
If we never repeat an edge, then we have a trail. The previous walk is not a trail because we backtrack through ab.

In contrast, (a, e, c, d, e) is a valid trail in our example graph, because although e appears twice, we get to it via different edges each time.

If we never repeat a vertex, then we have a path. For instance, (c, d, e, a, b) is a path that happens to involve all vertices.

However, if the path loops over from the final vertex back into the first one, so the start and end are the same vertex, we call it a cycle.

So, vertices and edges are the building blocks of graphs, giving rise to walks, trails and paths.

With these notions, we can start to ask general questions about the structure of a graph. One question is connectivity, that is, which vertices are reachable from each other.

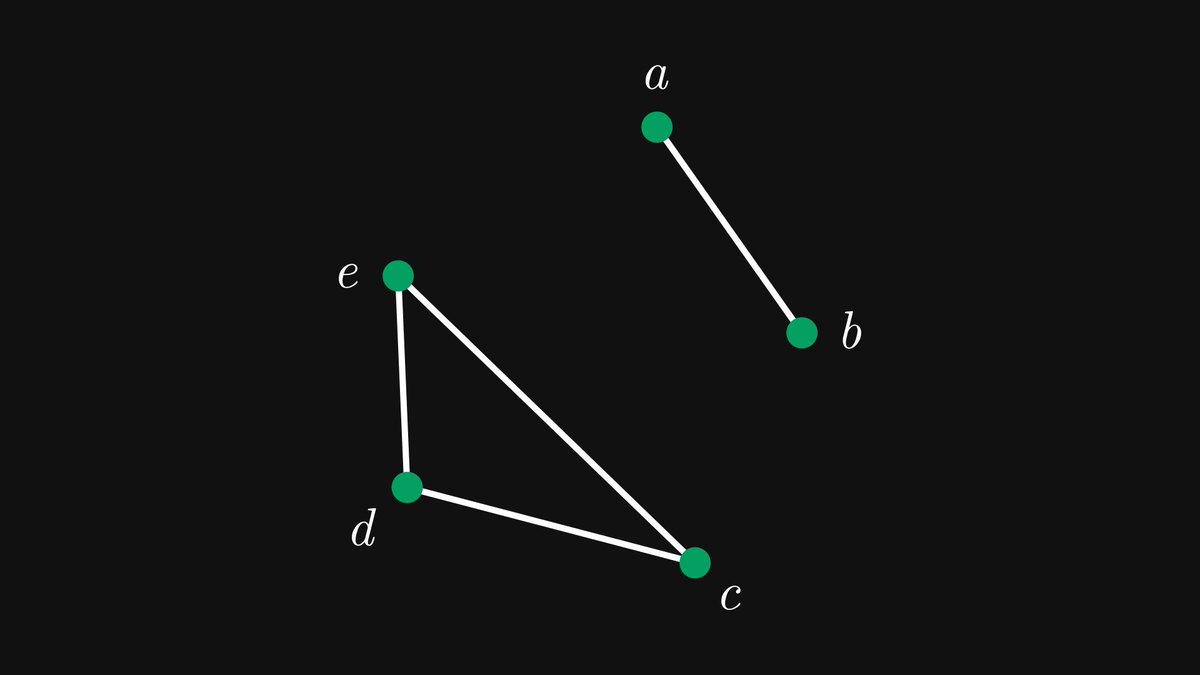
An interesting question regarding connectivity is how critical a vertex or edge is regarding connectivity.

If removing a single vertex (or edge) from a graph splits a connected component into two or more, then that vertex is called a cut vertex (or cut edge).

In the previous graph, the removal of vertex a (and its corresponding edges) produces five connected components, while the removal of vertex b produces three.

The removal of the edge ab only produces two connected components.

Next time, we’ll be looking at trees, arguably the most important data structure in computer science.

This thread is a collaboration with @alepiad, and is only 15% of the full post.

You can find it in the alt text of this image; it's worth a read.

If you have enjoyed this thread, share it with your friends and follow me for more no-nonsense top-tier technical content!

(Or say something nice in the replies; otherwise, The Algorithm is going to banish this post into oblivion.)

https://twitter.com/TivadarDanka/status/1731634936191340843