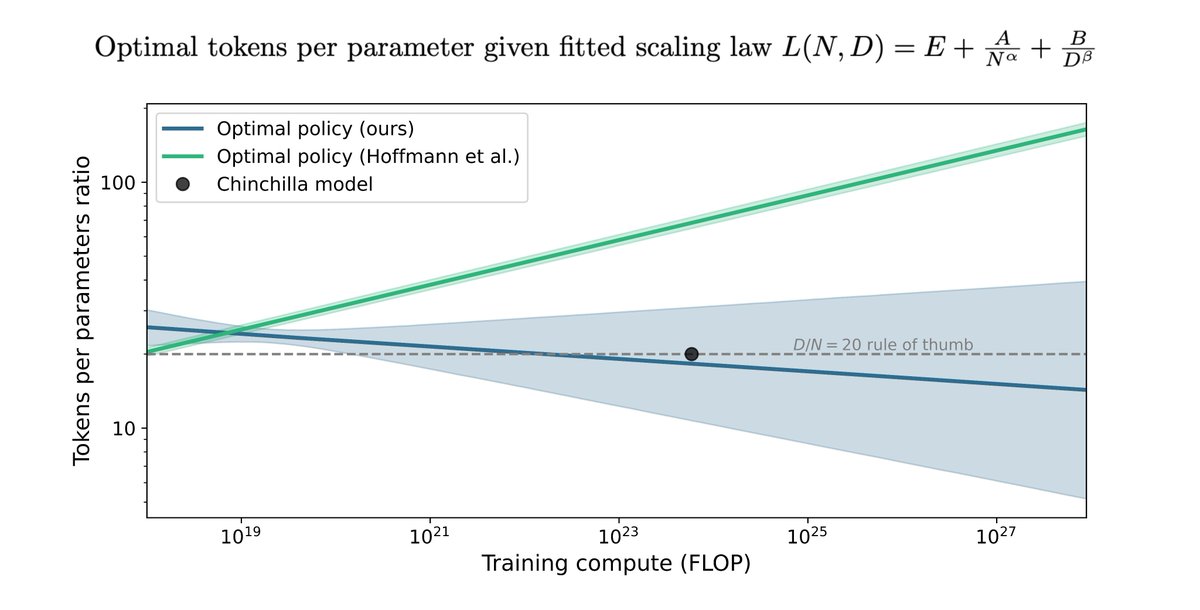
The Chinchilla scaling paper by Hoffmann et al. has been highly influential in the language modeling community. We tried to replicate a key part of their work and discovered discrepancies. Here's what we found. (1/9) 
We reconstructed the data by extracting the SVG from the paper, parsing out the point locations & colors, mapping the coordinates to model size & FLOP, and mapping the colors to loss values. This let us closely approximate their original dataset from just the figure. (2/9) 

When we fit their parametric scaling law, we get strikingly different estimates (Chi-squared p-value <1e-60!). The differences are significant for the data-scaling coefficient β and the irreducible loss E. (3/9) 

Hoffmann et al.'s estimated scaling law fits the reconstructed data very poorly compared to ours. Their residuals are not centered at 0 at all! Our model achieves a lower loss on 98% of data points. Clearly, their model does not fit the data. (4/9) 

Hoffmann et al. also report extremely narrow confidence intervals for some key parameters. We calculate that you’d need about 600,000 data points to nail it down that precisely. By contrast, they likely had ~400. (5/9) 

Moreover, Hoffmann et al.'s estimates imply a scaling policy inconsistent with their other results and the token-to-parameter ratio used for Chinchilla. Our estimates align better with these and have more reasonable uncertainty. (6/9) 
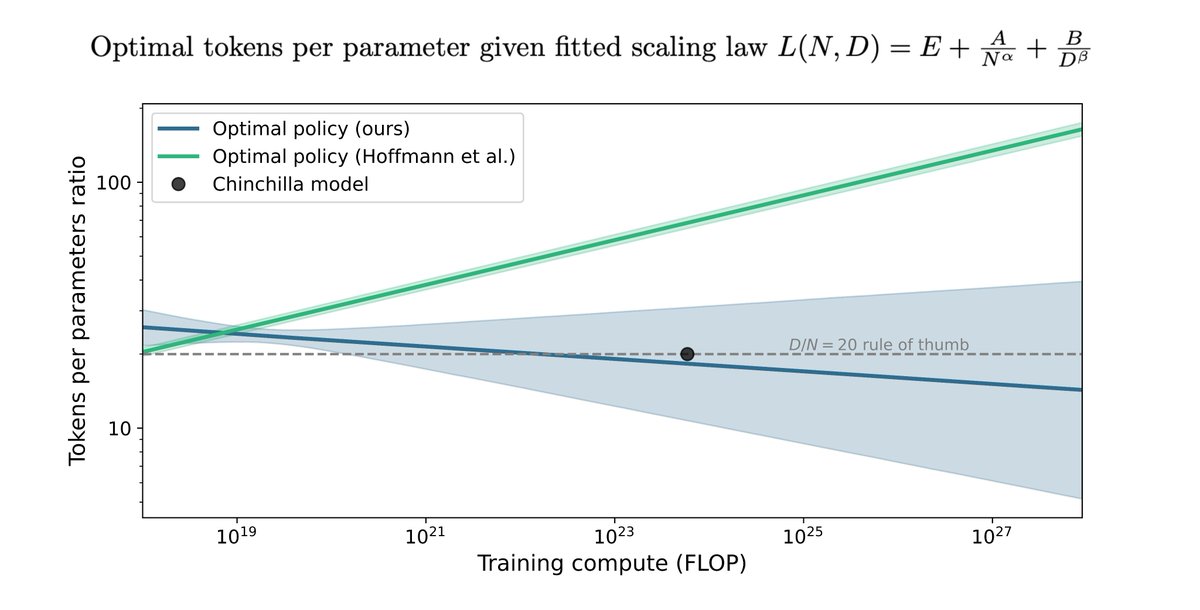
Hoffmann et al.’s paper has been highly influential in the language modeling community. Our analysis highlights some potential issues that warrant clarification. (7/9)
We have asked the authors for assistance, but we haven’t been able to get a response. (8/9)
Here is a short preprint that describes our findings in more detail: (9/9)
Worked on this togther with @EgeErdil2 , @MatthewJBar, and @justjoshinyou13.arxiv.org/abs/2404.10102
Worked on this togther with @EgeErdil2 , @MatthewJBar, and @justjoshinyou13.arxiv.org/abs/2404.10102
You can reproduce all our work:
Extracted data:
Code to reproduce results:
Code to extract data from SVG: github.com/Besiroglu/data…
colab.research.google.com/drive/1VAVVYRK…
colab.research.google.com/drive/1ROmEyJH…
Extracted data:
Code to reproduce results:
Code to extract data from SVG: github.com/Besiroglu/data…
colab.research.google.com/drive/1VAVVYRK…
colab.research.google.com/drive/1ROmEyJH…
• • •
Missing some Tweet in this thread? You can try to
force a refresh