Thread by @itsArmanJr

حتما براتون پیش اومده تو سایت‌های مختلف چیزی رو سرچ کنید ولی نتایج از زمین تا آسمون فرق داشته با اونی که تو ذهنتون بوده. واقعا چرا سرچ اکثر سایت‌ها اینقدر بده؟
تو این رشتو نگاهی می‌کنیم به دیجی‌کالا و می‌بینیم چطور با یه کم جبرخطی میشه تجربه جستجوی محصولات رو کلا متحول کرد.

قضیه از اینجا شروع میشه که می‌خوای برای پارتنرت کادو بخری. دیجی‌کالا رو باز می‌کنی، تو نوار جستجو می‌زنی ماتیک (چون اون لحظه بجای کلمه رژ لب، ماتیک تو ذهنت بوده). اینتر می‌زنی و منتظری چند صفحه رژ لیست شه تا از بینشون انتخاب کنی؛ اما تنها چیزی که میاد بیلاخه.

بعد عصبانی می‌شی و شروع می‌کنی به عرق کردن. ای بابا دستمال کاغذی ندارین که تو خونه. سرچ می‌کنی کلینکس. جز یه دونه که اونم برندش تشابه اسمی داره هیچ نتیجه‌ای نمیاد.

دیگه میگی آقا ولش کن خونسرد باش. یه ذره سر خودمو با فیلم و سریال گرم کنم بجای حرص خوردن. فیلم دیدن بدون چیزی خوردن مگه میشه؟ سرچ می‌کنی چس فیل. اما بازم جای دیگه‌ای از فیل تو نتایج منتظرته. لیپتون؟ صفر کالای موجود از چای کیسه‌ای.

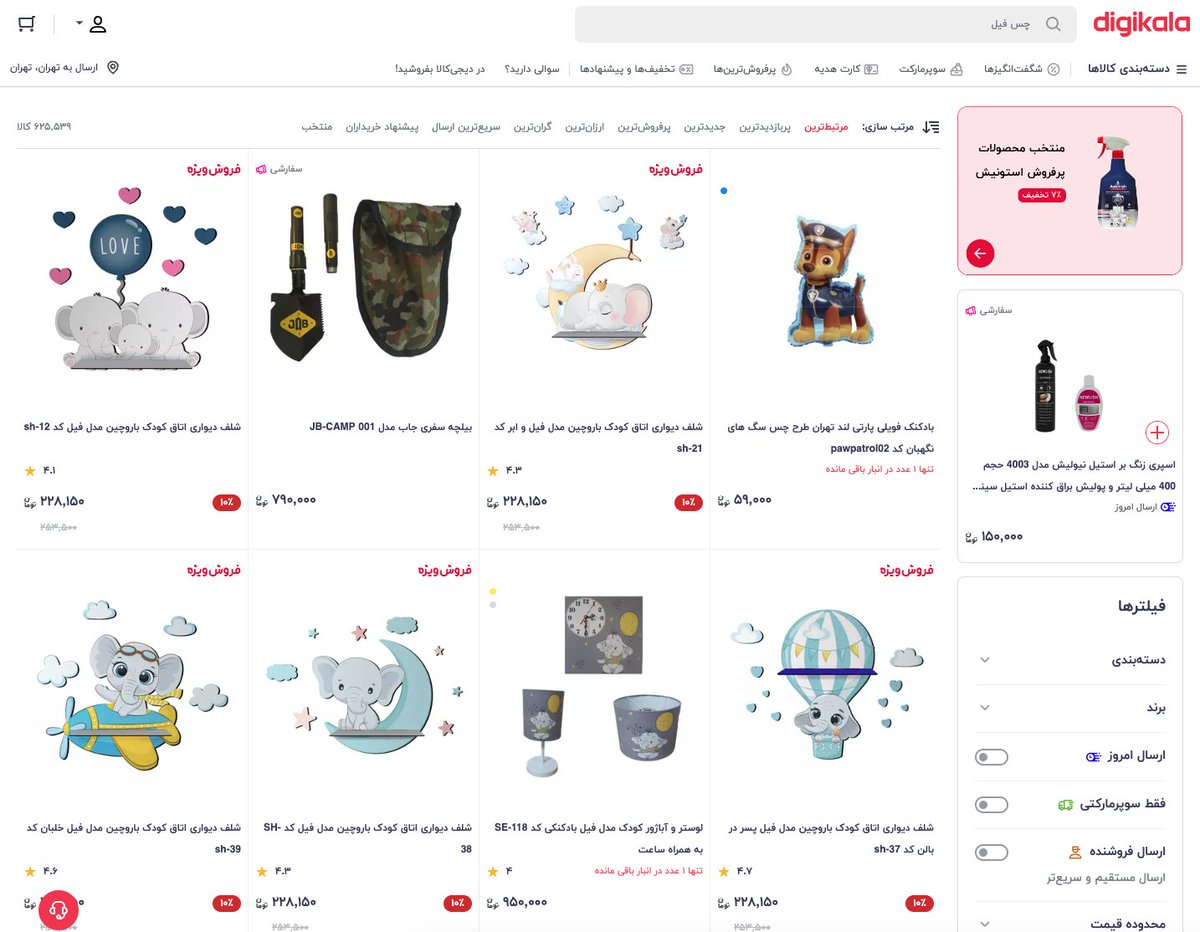
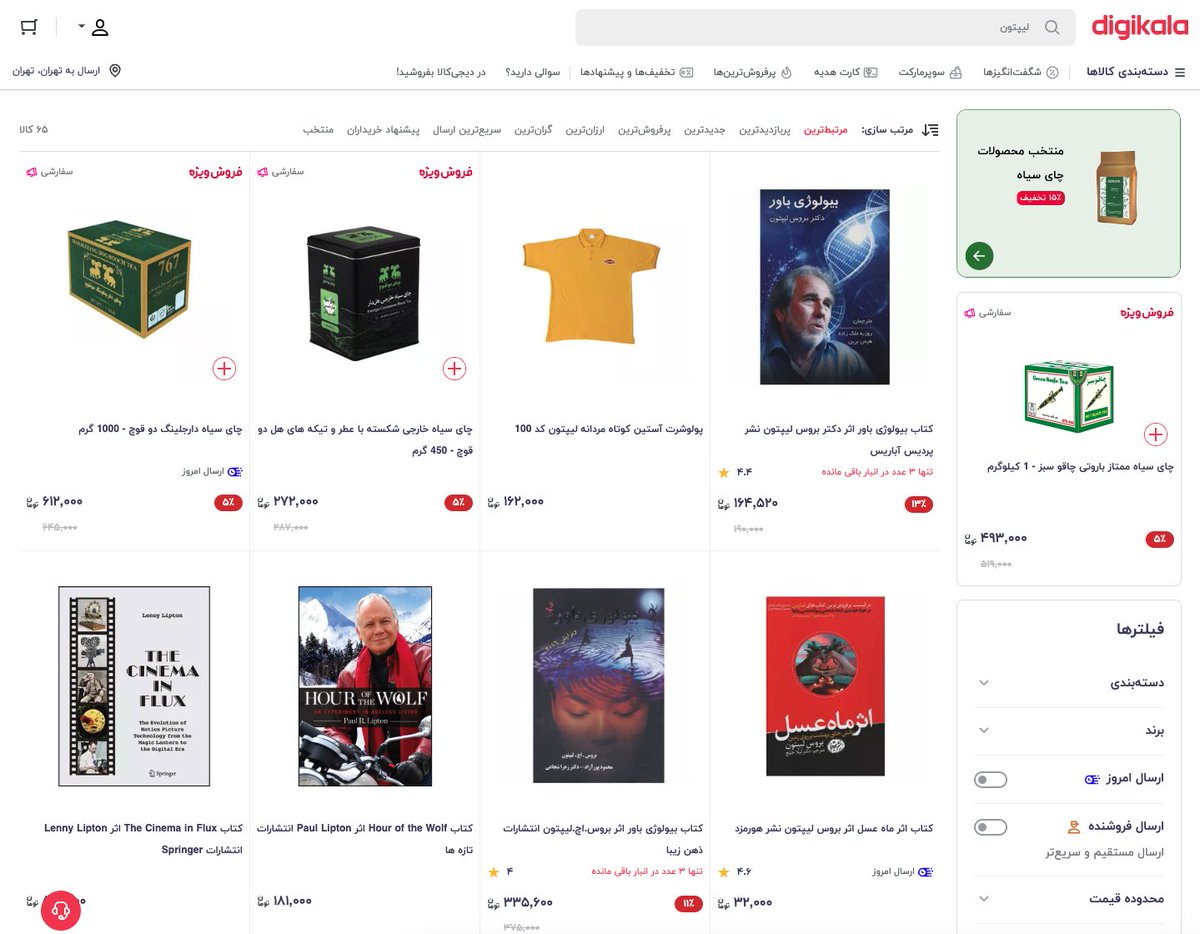
این قضیه راجع به کلمات دیگه هم هست. می‌زنی سامسونت گوشی موبایل سامسونگ میاد، استند تلویزیون کلا دوتا میز تلویزیون موجود میاره، تلفن ثابت بجای رومیزی صفر نتیجه، چاپگر هم با اینکه خیلی کم تو روزمره بکار میره ولی به‌هرحال معادل فارسی رسمی پرینتره که اونم تو دیجی‌کالا صفر نتیجه داره.

شاید خود من هیچوقت ماتیک رو جای رژ و لیپتون رو جای چای کیسه‌ای به کار نبرم ولی تا چه اندازه میشه مطمئن بود کل ایران با هر سن و سلیقه، یکسان سرچ می‌کنن؟ مطمئنا صدها محصول وجود داره که به چند اسم مختلف تو جوامع مختلف صدا میشه.

خیلی مثال دیگه علاوه بر اینها هست که نشون میده الگوریتم سرچ تو دسته‌بندی کلمات هم‌معنی و اجناس معادل، ضعف جدی داره.
چرا این اتفاق میوفته؟
راهکار کلی‌ای که برای پیاده‌سازی سرچ تو اکثر شرکت‌ها وجود داره استفاده از Elasticsearch هست.

الستیک یه موتور جستجوی اوپن‌سورس و خیل خفنه که برای نگهداری و تحلیل دیتا ازش استفاده می‌شه. وارد جزییات نمی‌شم اما اینو بدونین که از یه ساختار به اسم Inverted Index استفاده می‌کنه که داکیومنت‌هارو بر اساس «کلیدواژه» و فراوانی وزنی TF-IDF ذخیره و پردازش می‌کنه.

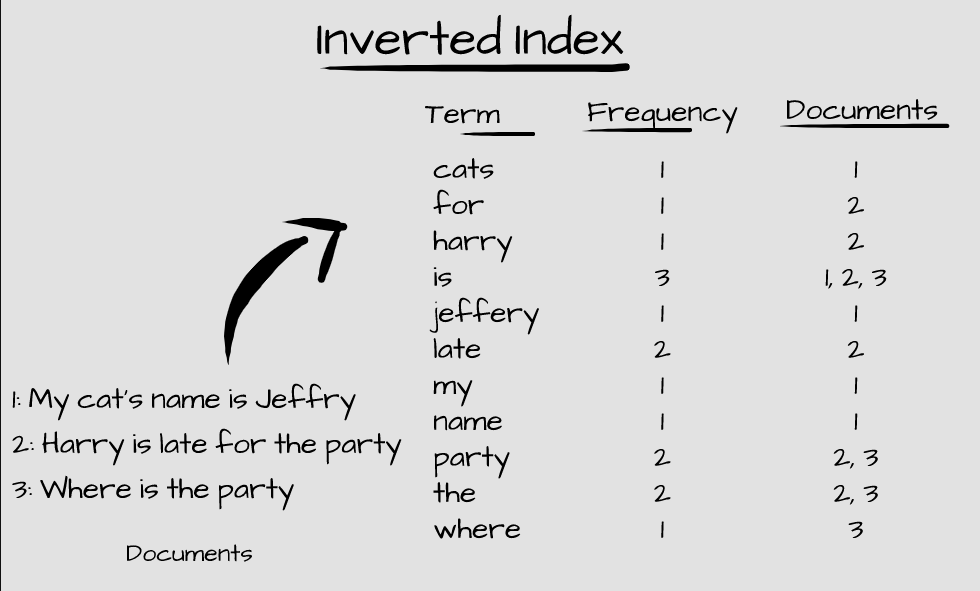
مشکل همینجاست که داریم از کلیدواژه‌ها استفاده می‌کنیم و موتور جستجوی ما هیچ درکی از اینکه چاپگر و پرینتر در واقع یک چیزن نداره.
حالا راه حل چیه؟ اولین چیزی که به ذهن می‌رسه داشتن یه دیتابیس از کلمات هم‌معنیه. اما کار تمیزی نیست چون تعداد کالاها زیاده و دیتابیس باید آپدیت بمونه.

ما باید راهی پیدا کنیم که متوجه منظور و مفهوم اون کلمه یا عبارت بشیم تا بفهمیم واقعا کاربر دنبال چی داره می‌گرده. بریم سراغ ریاضی 😁
از زمان مدرسه یادمونه که جای یه نقطه در صفحه رو با مختصات [x,y] نشون می‌دادیم. به همین ترتیب یه نقطه در فضا [x,y,z]. حالا جای چند نقطه در صفحه چی؟

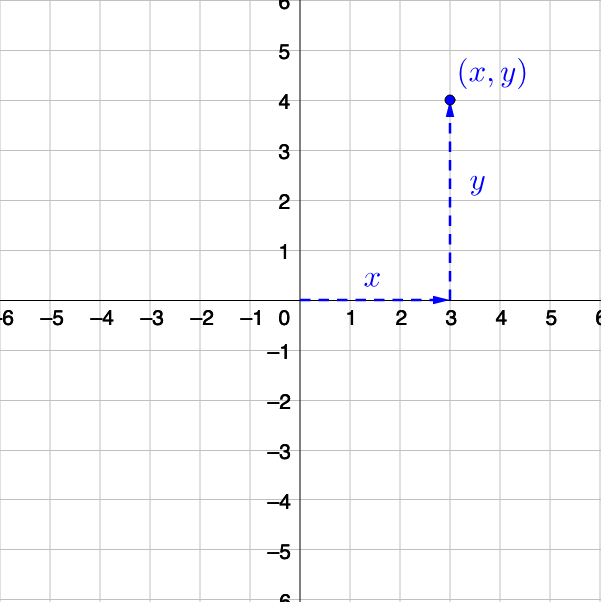
برای نمایش n نقطه در فضای ۲ بعدی به ماتریسی احتیاج داریم که هر ستون، نشانگر هر کدوم از نقاط‌مون باشن و سطر اول مقدار طول (x) و دوم عرض (y) اون نقاط. بعنوان قرارداد، هر نقطه رو هم به شکل فلش (بردار یا vector) ای که از مبدا میره اونجا در نظر بگیرید. به این شکل:

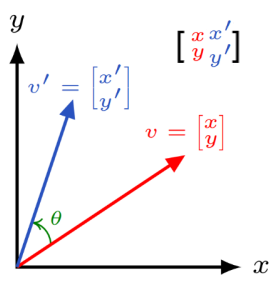
حالا فرض کنید از ما می‌پرسن فاصله نقطه p از q چقدره. خیلی ساده جوابش میشه اندازه برداری که از p میره به q. قضیه فیثاغورث یادتونه که تو یه مثلت قائم الزاویه وتر به توان ۲ می‌شد جمع توان دوی اضلاع؟ دقیقا به همون شکل اندازه این بردار که الان وتر مثلثه در میاد.

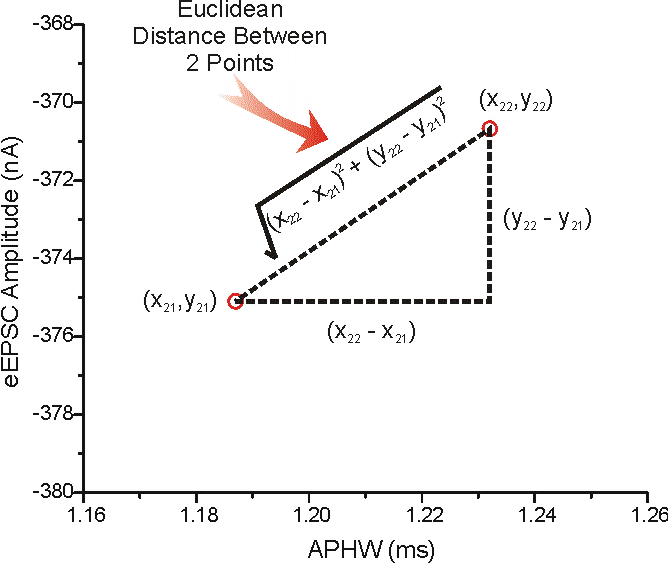
الان توانایی سنجش فاصله بین هر دو نقطه تو فضا رو داریم. یه نقطه جدید میاد وسط. از ما می‌پرسن نزدیک‌ترین نقطه‌ها به این چیه؟ فاصله همه نقاط از این نقطه جدید رو درمیاریم و اونایی که کمترین فاصله رو دارن معرفی می‌کنیم. در واقع میشه همسایه‌های اون نقطه تو یه دایره (بهش میگن KNN).

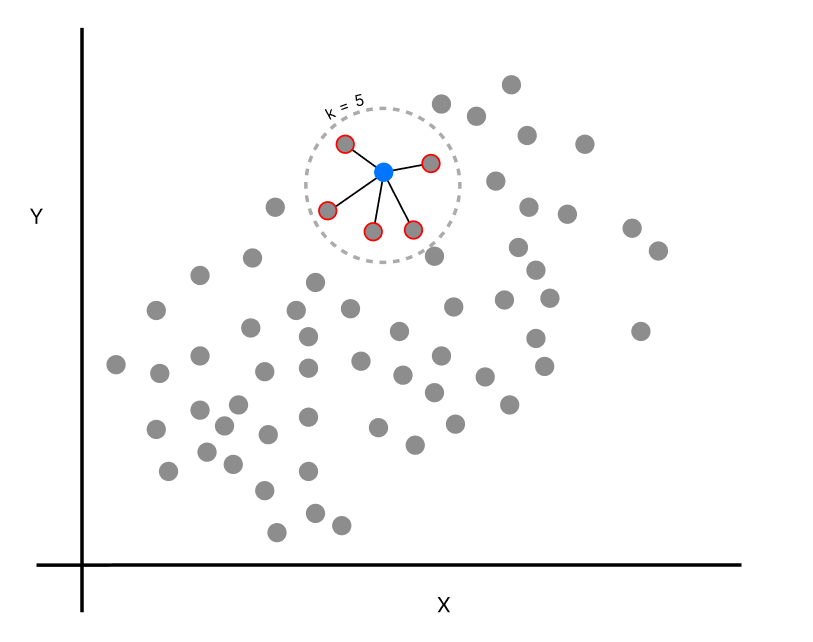
حالا به یه بعد بالاتر فکر کنید. توی یه فضای ۳ بعدی هم تمام این محاسبات برقراره با یه کم جزییات بیشتر. مثلا همسایه‌های یک نقطه جدید، بجای دایره میوفته توی یه کره به مرکز اون نقطه. تو ابعاد بالاترش هم همینطور.

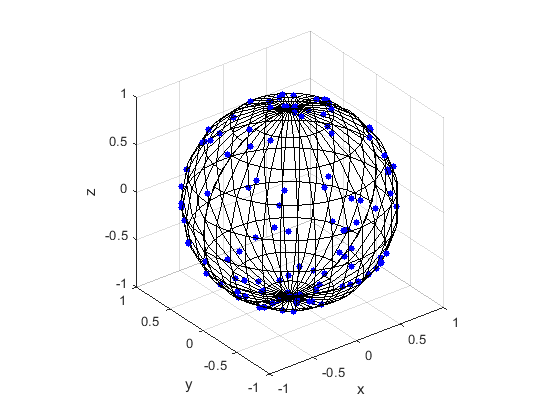
حالا بریم سراغ کار خودمون؛ فهمیدن مفهوم از متن.
تمام کلمات موجود تو یه زبان رو برمی‌داریم. مثلا ۵۰ هزارتا. همه رو پرت می‌کنیم تو یه فضای خیلی زیاد بُعدی مثلا n. هرکدوم تبدیل میشن به یه بردار n بعدی. همه رو کنار هم می‌چنیم بشکل ماتریس. هر ستون یک کلمه. بهش میگیم Embedding matrix.

عددی که تو هر سطر و ستون این ماتریس وجود داره اول رندومه اما مدل ما هرچقدر بیشتر که دیتا (مثل مقاله، داستان، کتاب،...) می‌بینه با یه سری فرمول ریاضی کم کم شروع می‌کنه به عوض کردن این اعداد (=یاد گرفتن). هر ورودی متنی مثل «بابا باد داد» وزن‌های کلمات بابا، باد و داد رو عوض می‌کنه.

هرچقدر مدل ما بیشتر یاد می‌گیره، یواش یواش کلمات چاپگر و پرینتر رو نزدیک به هم قراره میده چون مقالاتی که راجع به هرکدوم خونده خیلی شبیه بهم بوده؛ و کم کم به سمتی می‌ریم که هر «جهتی» از این فضای خیلی زیاد بعدی، انگار یک مفهوم رو داخل خودش داره.

بعنوان یه مثال دیگه، مدل GloVe که روی مقالات ویکی‌پدیا آموزش دیده رو اگر در نظر بگیریم، توش کلمات «ساختمون»، «آسمان‌خراش»، «سقف» و «ساخت» نزدیک به هم قرار می‌گیرن.

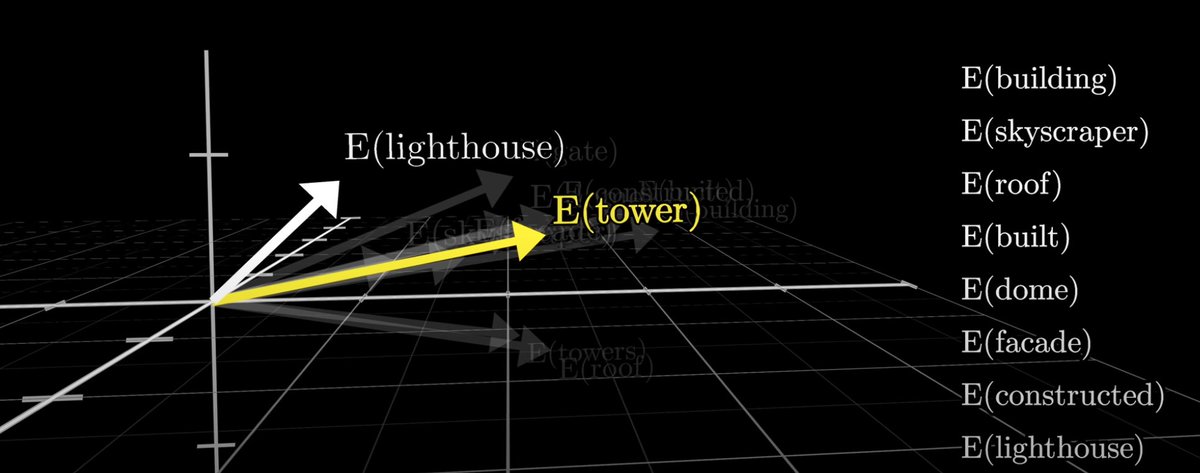
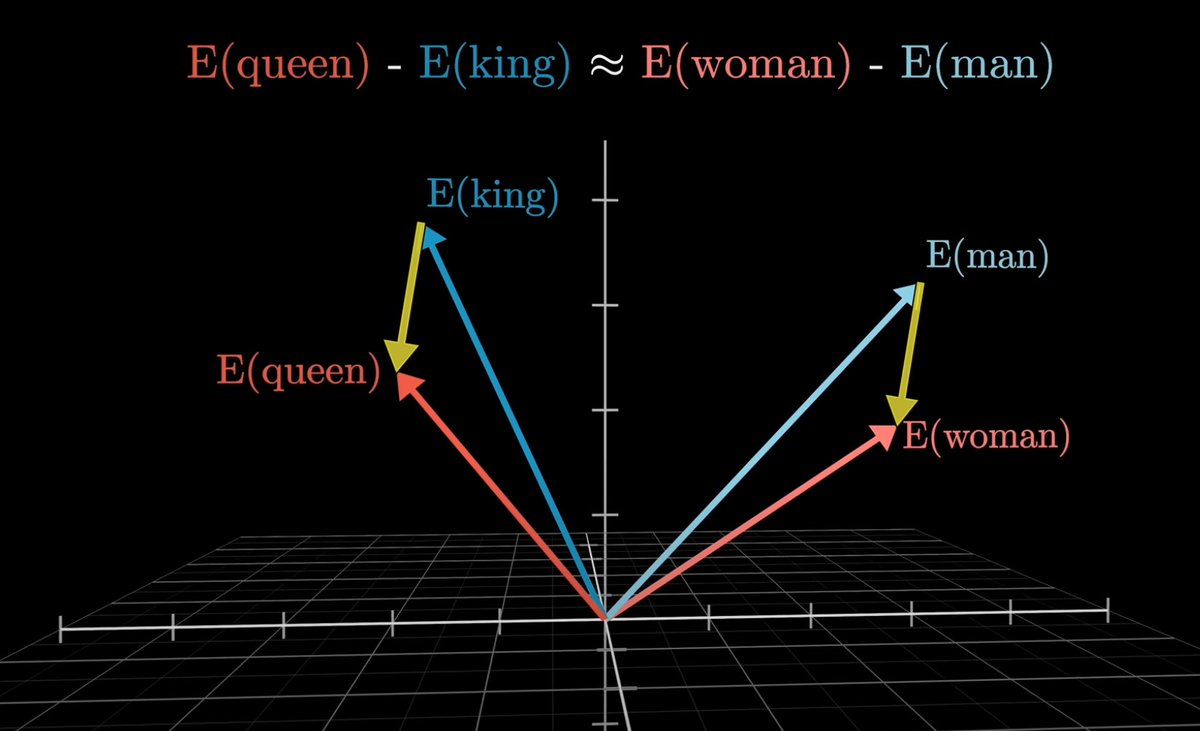
اما نکته جالب اینه که ما میتونیم اعمال ریاضی روی این کلمات انجام بدیم. تفریق برداری «مرد» از «زن» یه بردار جدید توی فضاست (از انتهای کلمه مرد به کلمه زن وصل کنین). این بردار خیلی شبیه‌هه به برداری که از تفریق «شاه» از «ملکه» بدست میاد.
انگار اون جهت برداری (زرد)، مفهوم جنسیته.

توی این معادله اگر کلمه شاه رو ببریم سمت راست، میتونیم خود کلمه ملکه رو بدست بیاریم: جمع شاه با زن منهای مرد. پس الان یه مدلی داریم که میتونیم ازش بپرسیم پادشاه مونثی که مرد نیست چیه و جواب بگیریم ملکه. می‌بینید چقدر قشنگ مفهوم و معنی کلمات به ریاضی مدل شدن؟

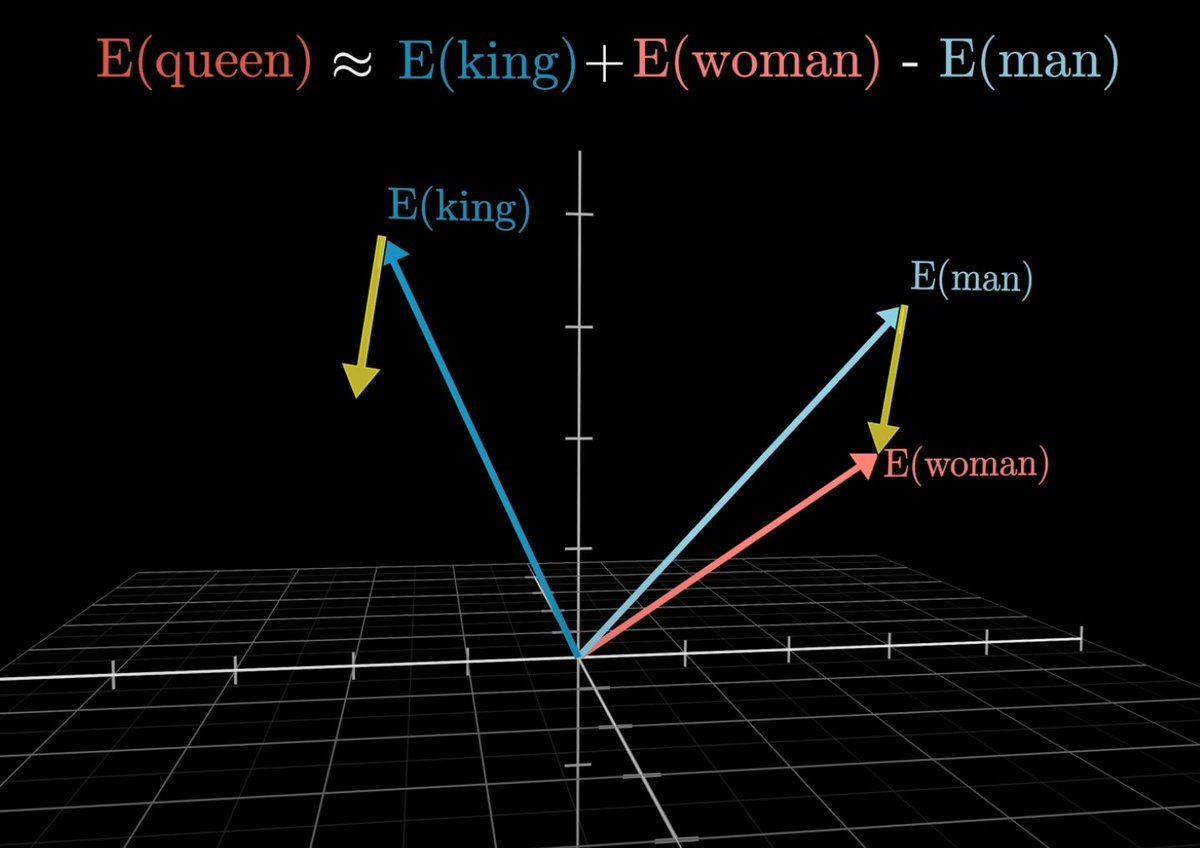
این کار رو بهش می‌گن word embedding. حالا فرض کنید توی این فضای چندبعدی، به‌جای کلمه، محصولات مختلف دیجی‌کالا باشن. product embedding.
به ازای هر کالا، عنوان محصول + توضیحاتش رو با استفاده از یه مدل زبانی بزرگ (که مثلا کل ویکی‌پدیای فارسی رو قبلا خونده) ببریم تو این فضا.

با اینکار، موفق می‌شیم محصولات شبیه به هم رو نزدیک به هم داشته باشیم. «لپ‌تاپ ۱۵.۶ اینچی MSI» کنار «کامپیوتر همه‌کاره ASUS» قرار می‌گیره بدون اینکه تو عنوان کالا اشتراکی داشته باشن. با اختلافی کم، احتمالا کالاهای دیجیتال و با یه فاصله زیاد لباس زنانه که شباهتی با اینا نداره هست.

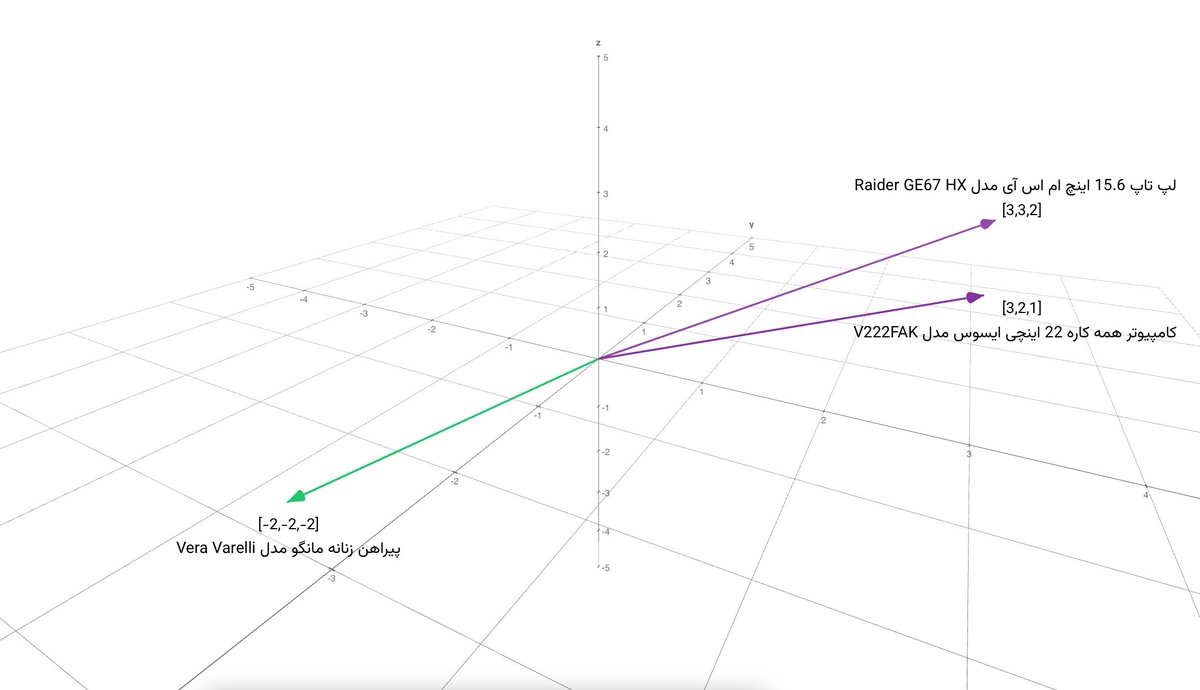
در نهایت، وقتی کاربر برای چیزی سرچ می‌کنه، ما اونو برمیداریم و مثل یه نقطه می‌ندازیم توی این فضا، با استفاده از KNN می‌بینیم چه محصولاتی تو نزدیک‌ترین همسایگی این نقطه هستن و همونا رو نشون میدیم.
اینطوری با سرچ چاپگر میشه تو نتایج پرینترها رو دید. به همین راحتی به همین خوشمزگی 😁

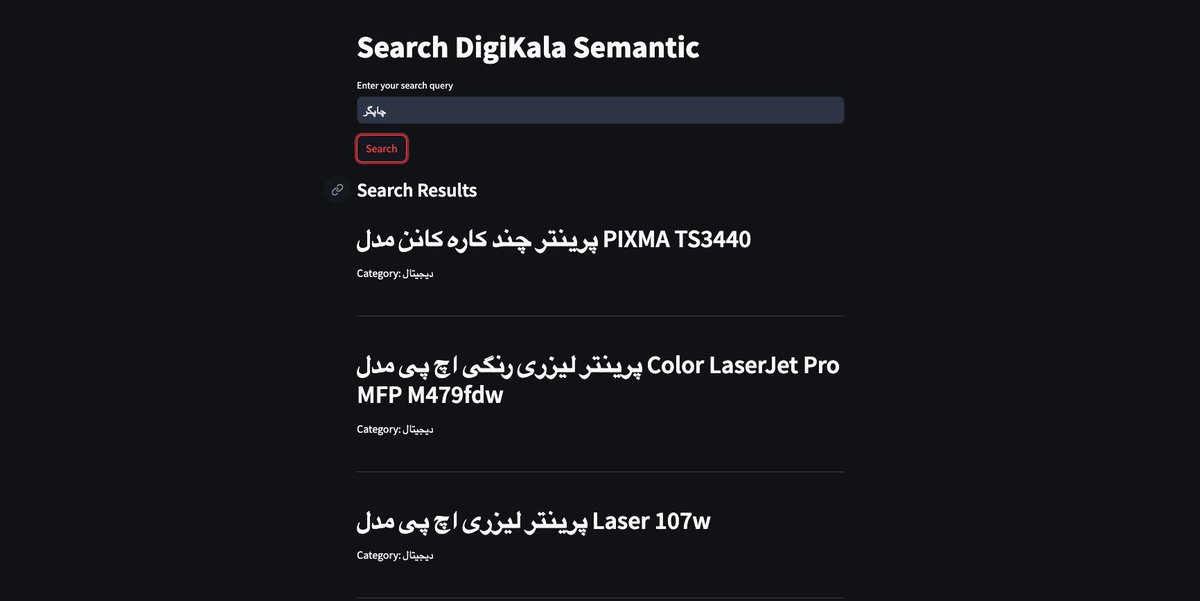
من با استفاده از دیتاست دیجی‌کالا () یه دمو از کل این فرایند ساختم و خیلی چیز جالبی شد. کدش رو گیت‌هابم هست. دوست داشتید امتحان کنید: البته هنوز خیلی جای بهتر شدن داره.kaggle.com/datasets/radea…
github.com/ArmanJR/Digika…

در آخر، رفرنس و نکته:
- ویدیو
- من سعی کردم به ساده‌ترین شکل ریاضی‌ش رو بگم و شاید نادقیق حرف زده باشم. با پوزش از اساتید لطفا ایده کلی رو بچسبید :))
- پیاده‌سازی این تو مقیاس دیجی‌کالا منابع زیادی می‌خواد اگر پیاده نمیشه شاید فعلا نمی‌صرفه لابد ¯\_(ツ)_/¯