Thread by @robertghrist

is there a finite-time singularity in fluids?
(euclidean 3-d euler/navier-stokes, smooth IC)
this is the data we collected at @CRMatematica today...

we voted on a scale from 0 to 10 where
0-nope! ==== 5-??? ==== 10-yeah!

here's the vote : euler in blue, navier-stokes in red...
but wait...there's more...

after voting -- in private! -- we then did a public vote-by-show-of-hands with yes/no/???
(all eyes were on terry tao, sitting in the back...)
then we did a second private vote...
can you guess how terry voted?

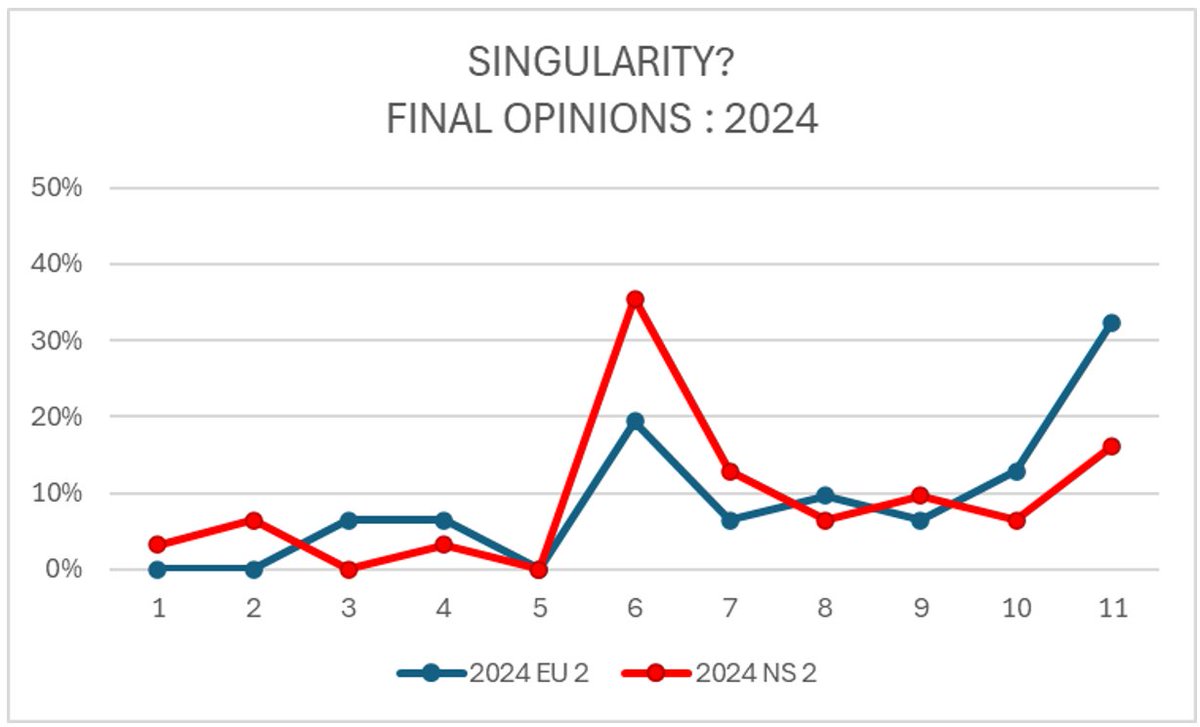
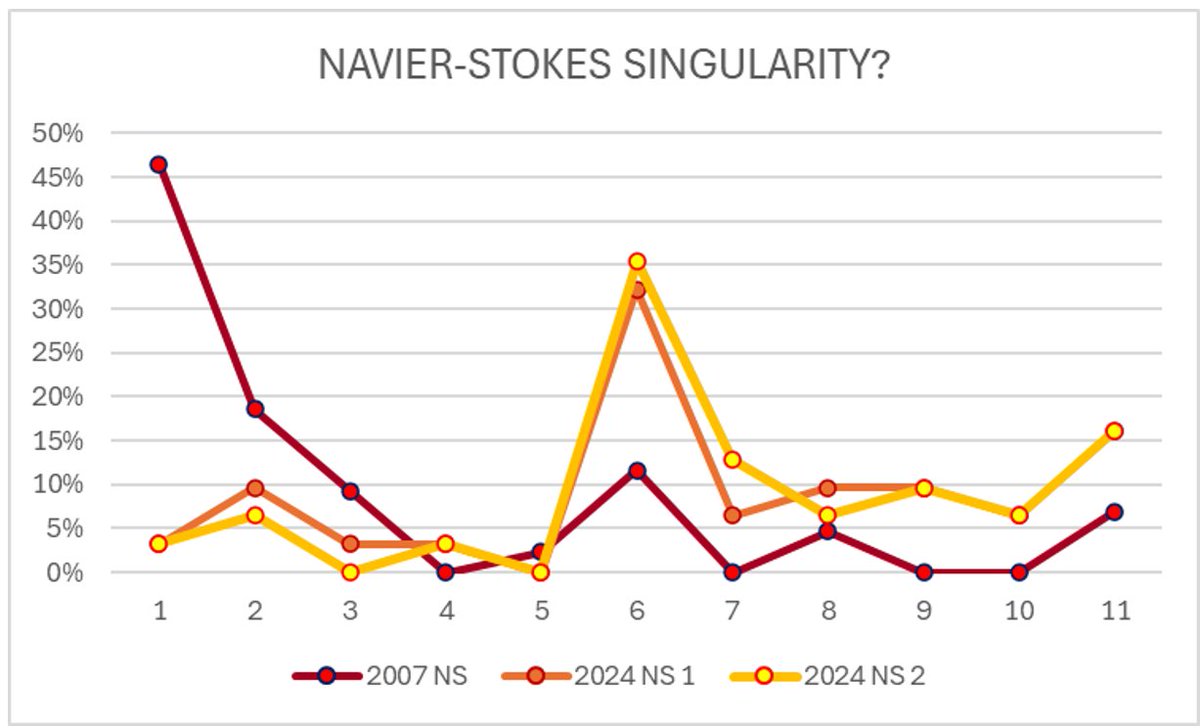
more data! the same exact question was asked at a meeting in 2007 at the 250th anniversary of the euler equations at a meeting of experts in Aussois, CH
(thanks to Kai Schneider for the data!)
here's what the data was in 2007

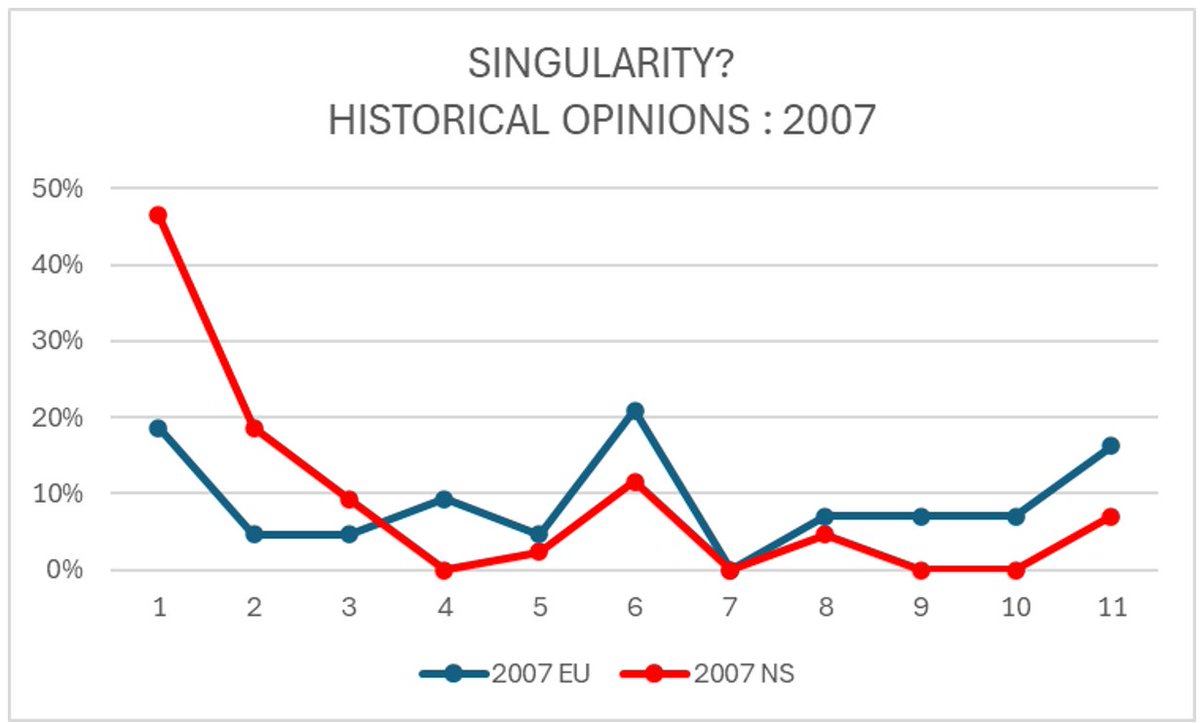
if you want to see the change in sentiment over time 2007 => 2024 1st vote => 2024 2nd vote, here's the euler equations...

and the same historical trends for navier stokes

so what have we learned?
* opinions have drifted more towards singularity
* opinions can change in real-time due to influence by neighbors -- very relevant to information flows...
* MS excel doesn't like indexing from 0 to 10

special thanks to kai cieliebak, @evamirandag , and kai schneider for suggesting and helping to get out the vote! (and for allowing me to conduct this little opinion dynamics experiment...)