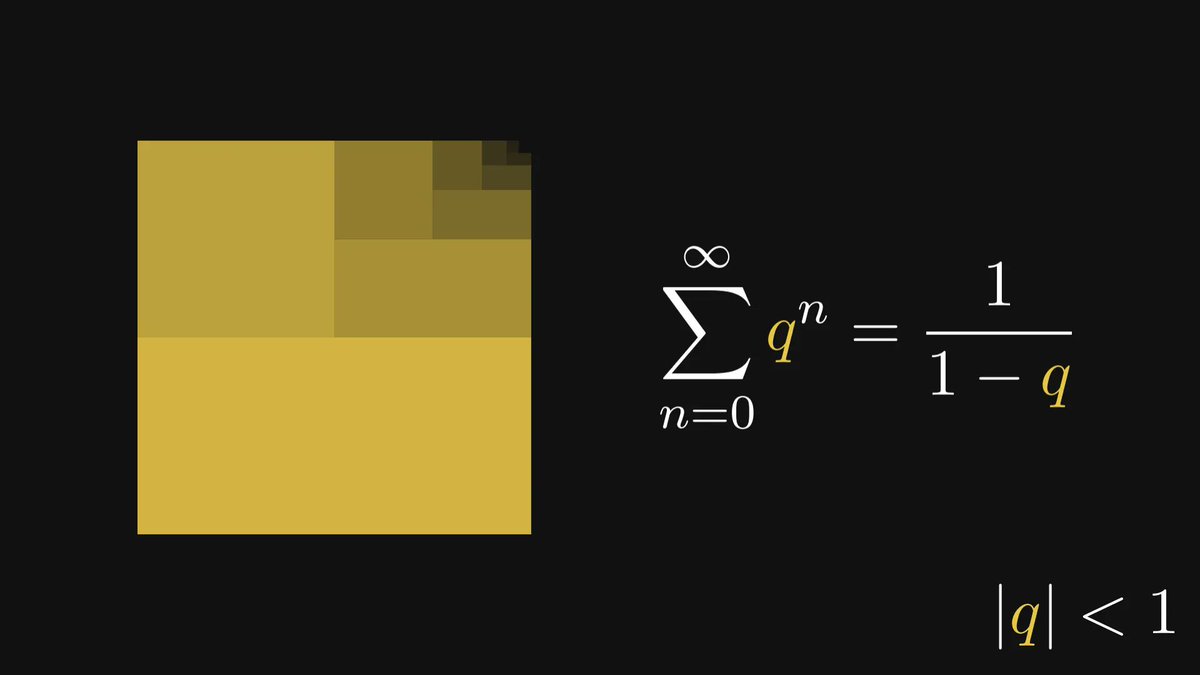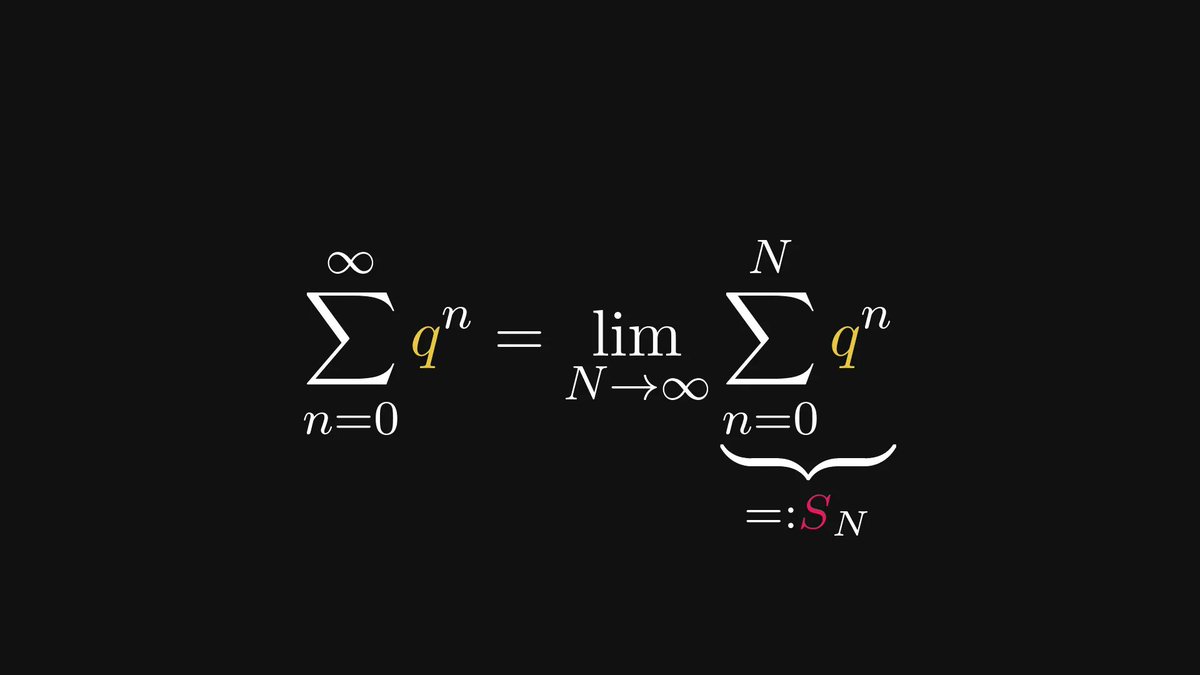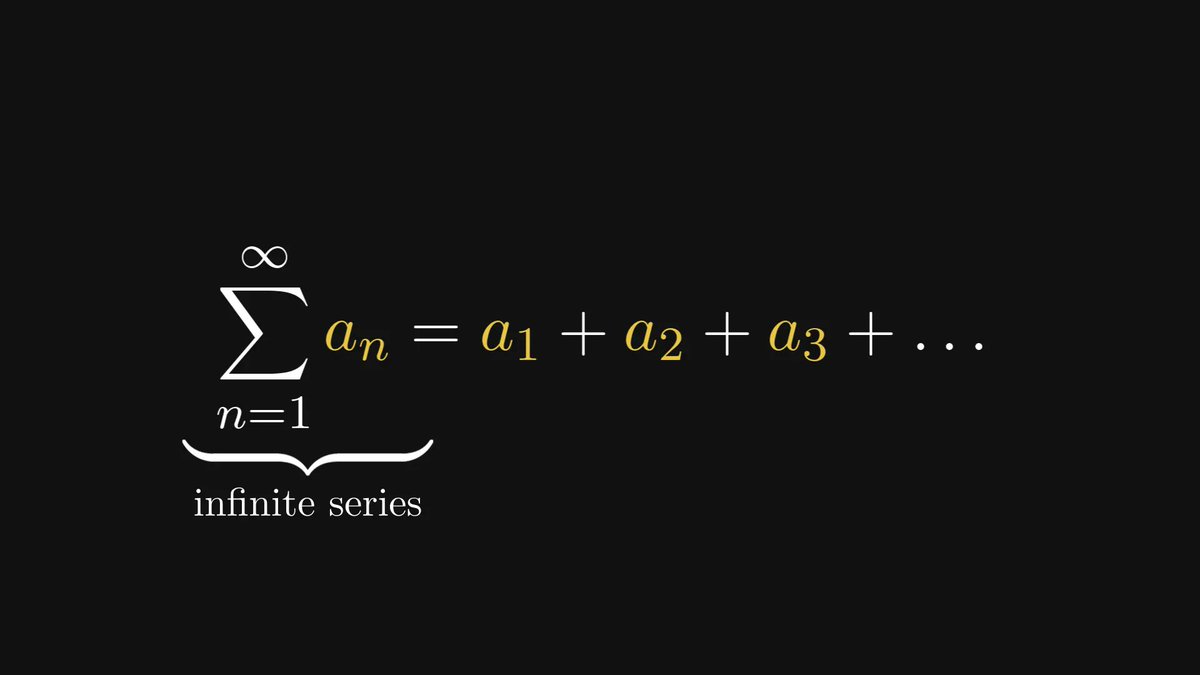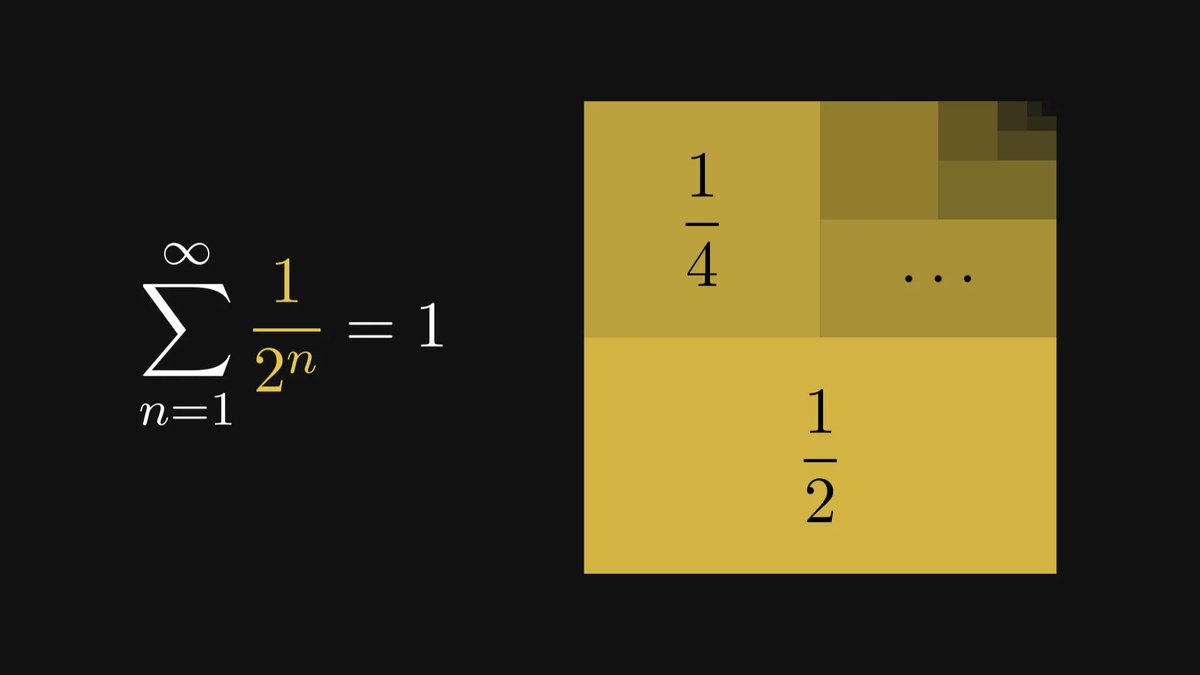How to build a good understanding of math for machine learning?
I get this question a lot, so I decided to make a complete roadmap for you. In essence, three fields make this up: calculus, linear algebra, and probability theory.
Let's take a quick look at them!
I get this question a lot, so I decided to make a complete roadmap for you. In essence, three fields make this up: calculus, linear algebra, and probability theory.
Let's take a quick look at them!
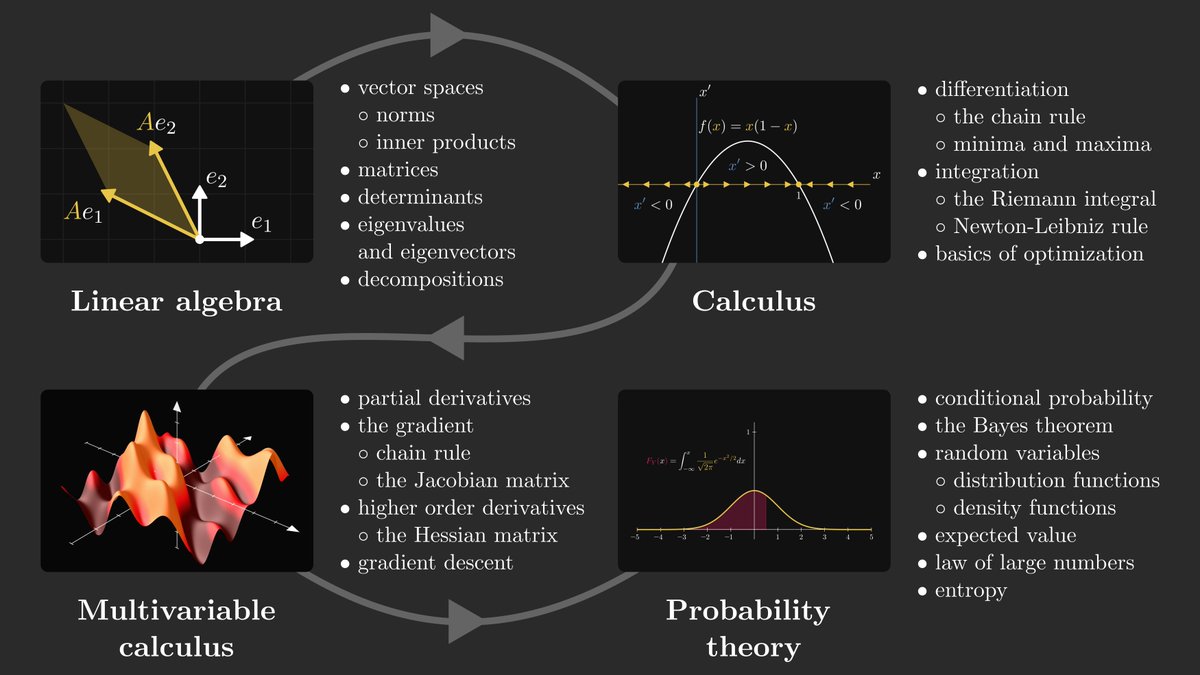
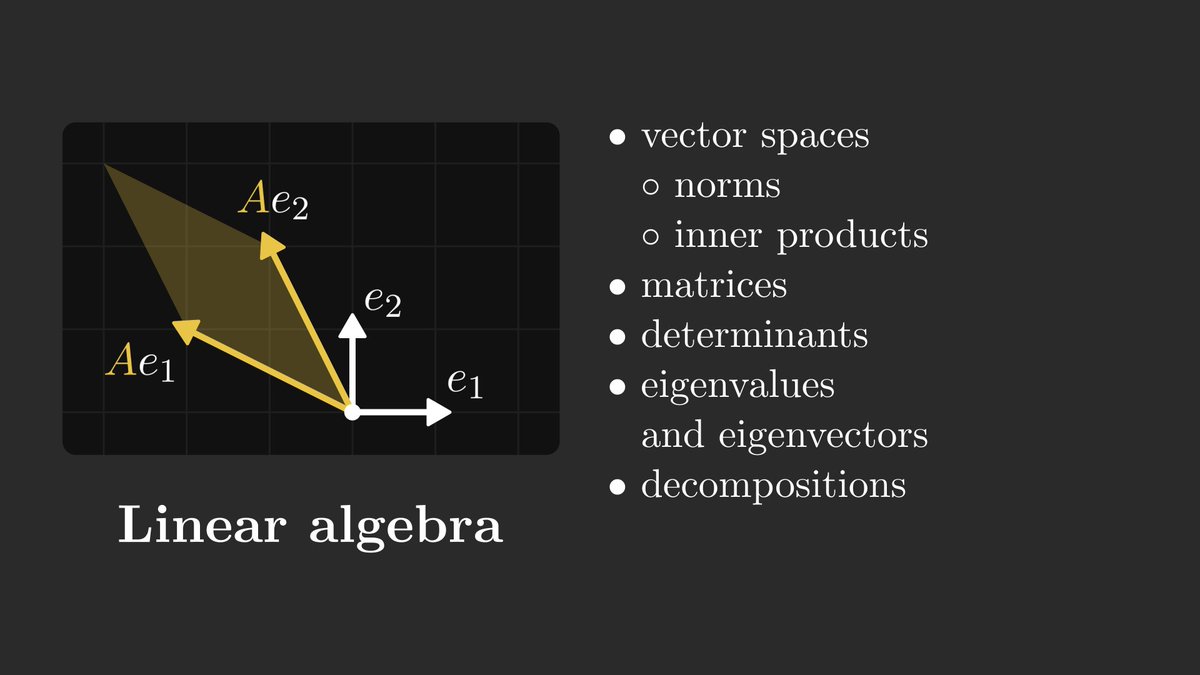
1. Linear algebra.
In machine learning, data is represented by vectors. Essentially, training a learning algorithm is finding more descriptive representations of data through a series of transformations.
Linear algebra is the study of vector spaces and their transformations.
In machine learning, data is represented by vectors. Essentially, training a learning algorithm is finding more descriptive representations of data through a series of transformations.
Linear algebra is the study of vector spaces and their transformations.
Simply speaking, a neural network is just a function mapping the data to a high-level representation.
Linear transformations are the fundamental building blocks of these. Developing a good understanding of them will go a long way, as they are everywhere in machine learning.
Linear transformations are the fundamental building blocks of these. Developing a good understanding of them will go a long way, as they are everywhere in machine learning.
2. Calculus.
While linear algebra shows how to describe predictive models, calculus has the tools to fit them to the data.
If you train a neural network, you are almost certainly using gradient descent, which is rooted in calculus and the study of differentiation.
While linear algebra shows how to describe predictive models, calculus has the tools to fit them to the data.
If you train a neural network, you are almost certainly using gradient descent, which is rooted in calculus and the study of differentiation.

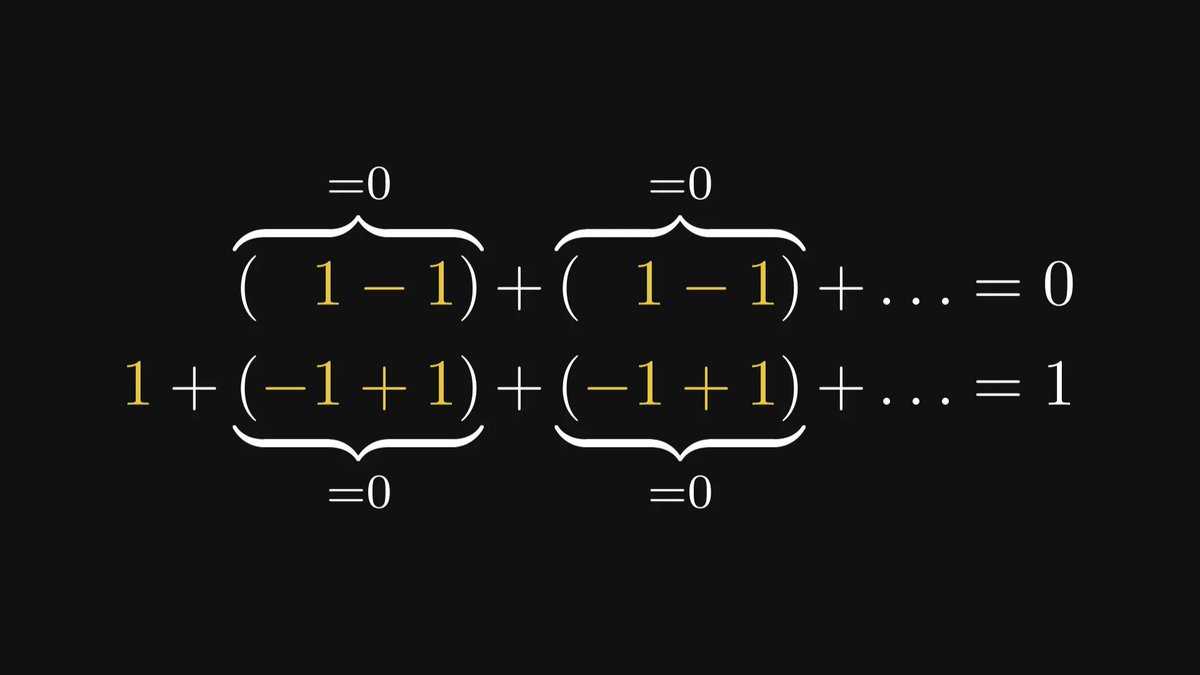
Besides differentiation, its "inverse" is also a central part of calculus: integration.
Integrals are used to express essential quantities such as expected value, entropy, mean squared error, and many more. They provide the foundations for probability and statistics.
Integrals are used to express essential quantities such as expected value, entropy, mean squared error, and many more. They provide the foundations for probability and statistics.
When doing machine learning, we are dealing with functions with millions of variables.
In higher dimensions, functions work differently. This is where multivariable calculus comes in, where differentiation and integration are adapted to these spaces.
In higher dimensions, functions work differently. This is where multivariable calculus comes in, where differentiation and integration are adapted to these spaces.

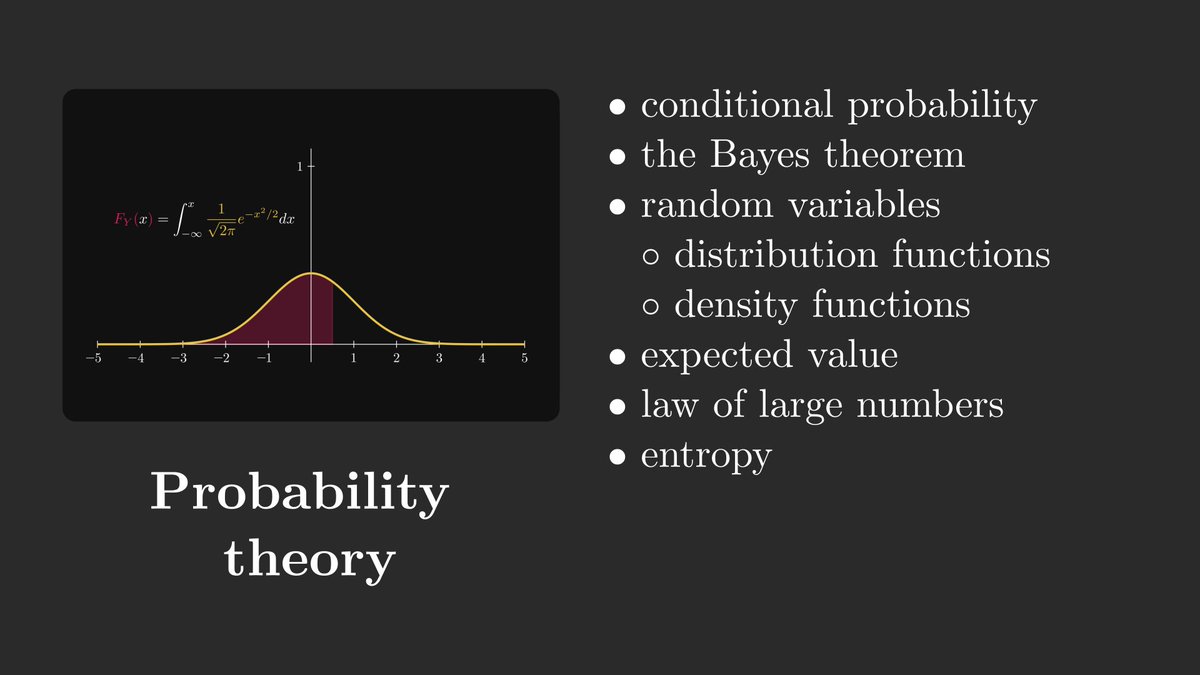
3. Probability theory.
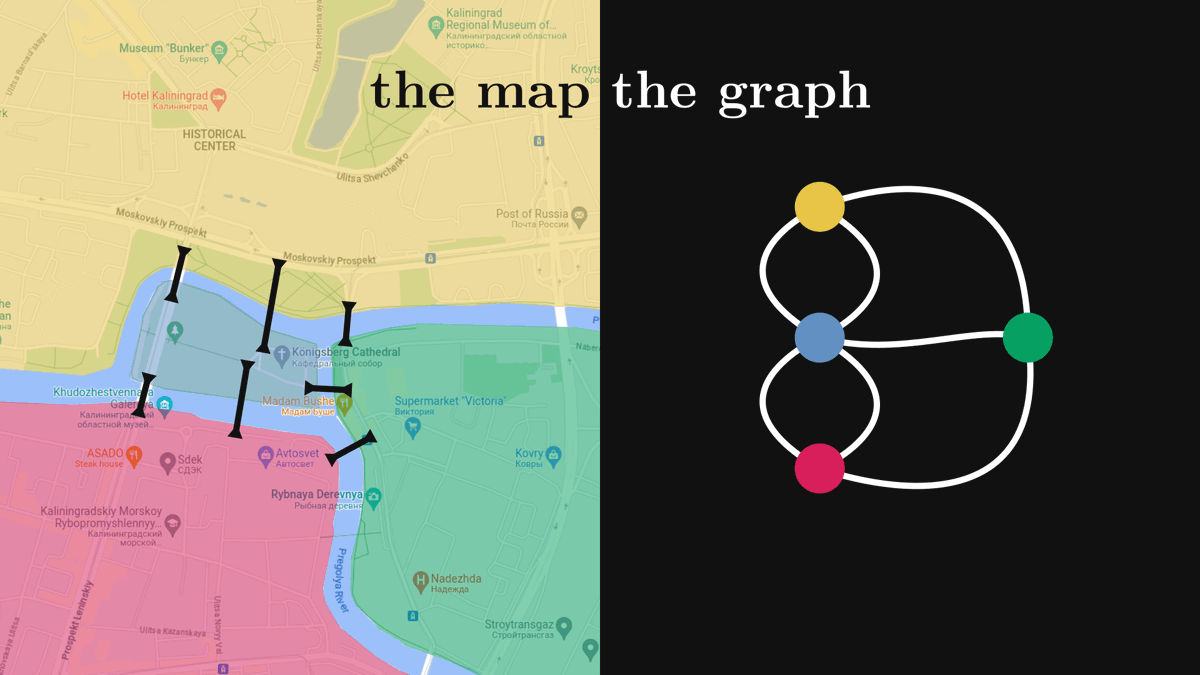
How to draw conclusions from experiments and observations? How to describe and discover patterns in them? These are answered by probability theory and statistics, the logic of scientific thinking.
How to draw conclusions from experiments and observations? How to describe and discover patterns in them? These are answered by probability theory and statistics, the logic of scientific thinking.
I know all of this because I spent five years writing a textbook about it. It'll be released in May, but you should preorder it now, as it's heavily discounted!
(The paperback version is currently $39.99, the final price will be $59.99 upon release.)
amazon.com/Mathematics-Ma…
(The paperback version is currently $39.99, the final price will be $59.99 upon release.)
amazon.com/Mathematics-Ma…
• • •
Missing some Tweet in this thread? You can try to
force a refresh