Thread by @jxmnop

new paper from our work at Meta!

**GPT-style language models memorize 3.6 bits per param**

we compute capacity by measuring total bits memorized, using some theory from Shannon (1953)

shockingly, the memorization-datasize curves look like this:
___________
/
/

(🧵)

this all started from a quest to come up with a proper measurement of model memorization

it's hard to compute *per-example* memorization, because models "share" info between datapoints

so we start with random uniform strings, where sharing isn't possible. and we get this:

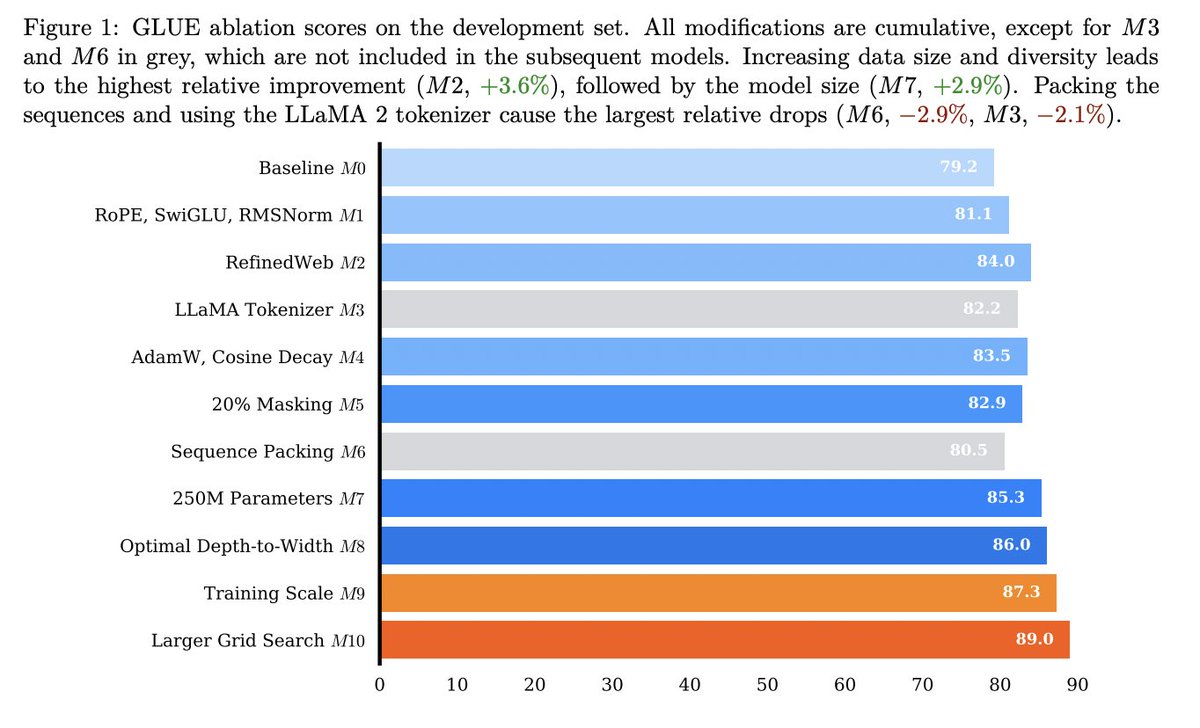
we then compute the capacity of different models
(GPT models with varying numbers of layers and hidden dimensions)

averaged over hundreds of models in fp32, we get the following curve, indicating a linear trend of around 3.6 bits-per-parameter, regardless of the exact details:

we train all of our models until they "saturate" which usually happens around 1M steps using a very large batch size

models memorize the same amount, regardless of training datasize

meaning they have fixed capacity and instead "spread it thinner" when trained on more examples

this gives a pretty good explanation into how models learn

in particular, it explains grokking

grokking occurs *exactly* when capacity saturates. this is where models can't perfectly fit every training example, so they have to share info bt examples in a smart way

we also compute capacity in bf16 and it drops a bit, to 3.5ish.

but that's a relative increase in bitwise usage (11% of bits or so to 22% of bits)

(my first thought was that transformers are doing a bad job of using params efficiently, but now im not sure. it's not *that* bad)

when we train on text data, the curves look different

models memorize examples to the extent that they can fit them in their parameters

beyond this point, the models discard per-example mem. in favor of shared info (*generalization*)

see how the lines start to slope downward:

- hrunning these experiments in a clean setting with perfectly deduplicated texts tells us a lot about privacy:

- once capacity is sufficiently saturated, the **test examples** are slightly more extractable than the training examples -- maybe extraction is a bit of a myth?
- the most extracted examples are the ones with really rare tokens, typically data from other languages that slipped into the training set
- membership inference is much easier than extraction

and finally we can compute membership inference success rate across all our models, ending up with this scaling law 👇

main takeaway: models trained on massive datasets (e.g. every LLM that comes out) can't memorize their training data

there's simply not enough capacity

this was a really fun project with lots of collaborators across various institutions. it took a long time but was definitely worth it, and i learned a lot!

also thanks to everyone who gave us feedback along the way :-)

now check out the paper: arxiv.org/abs/2505.24832