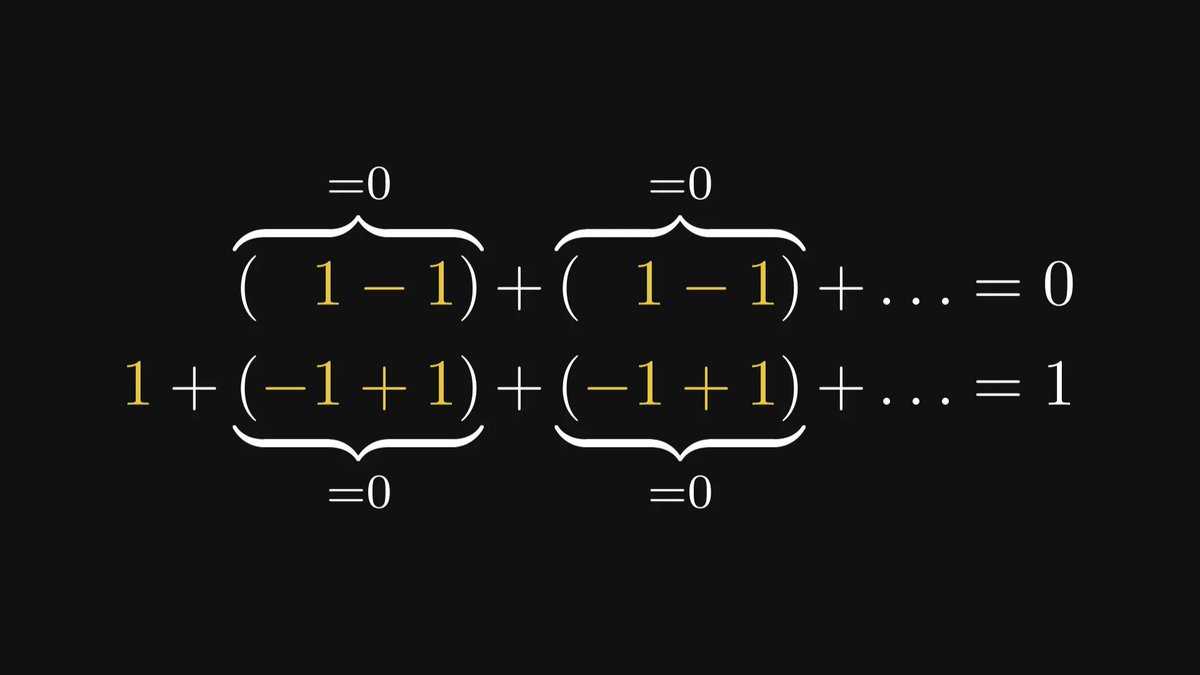
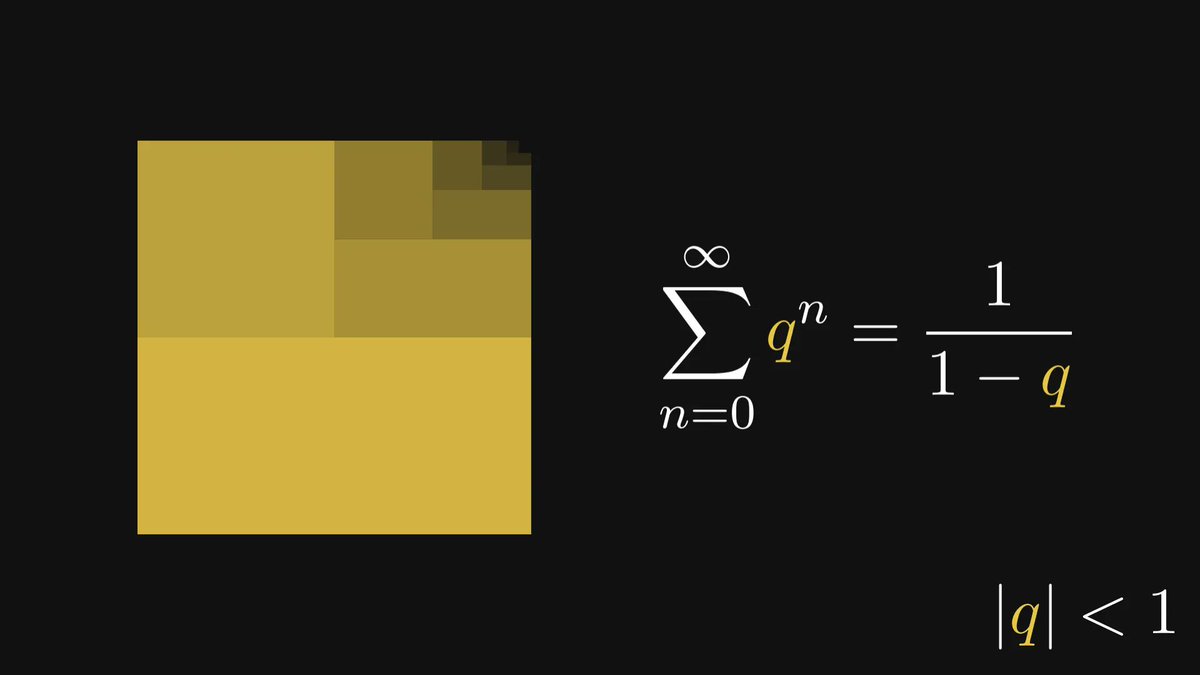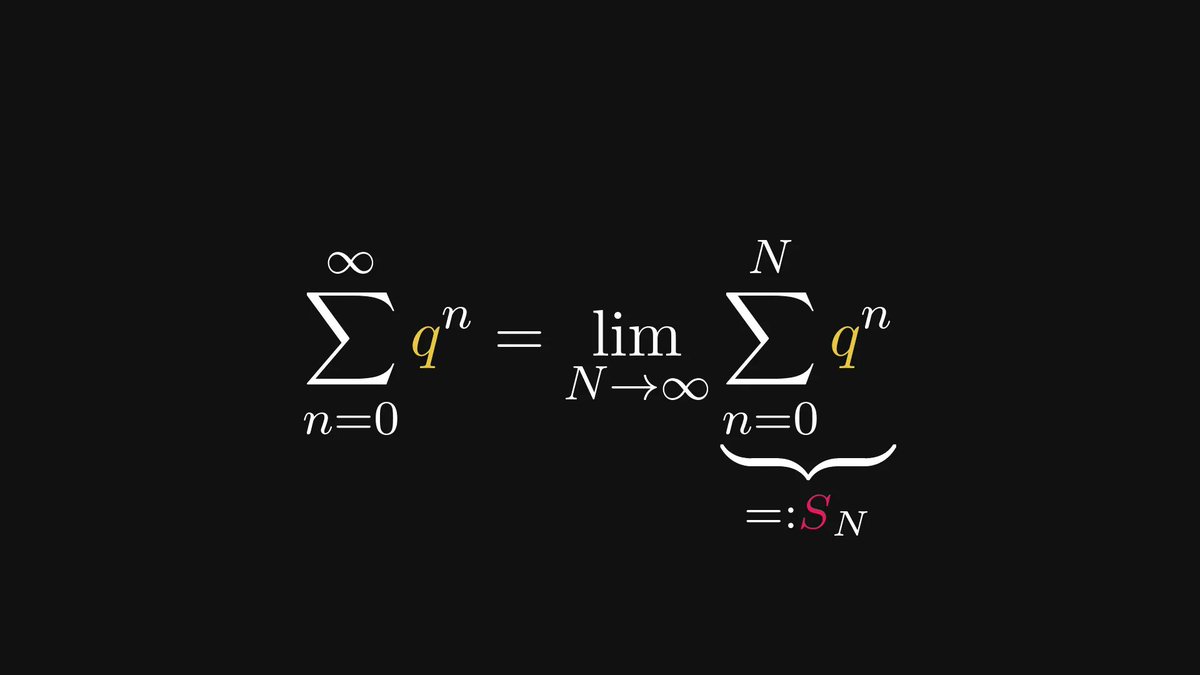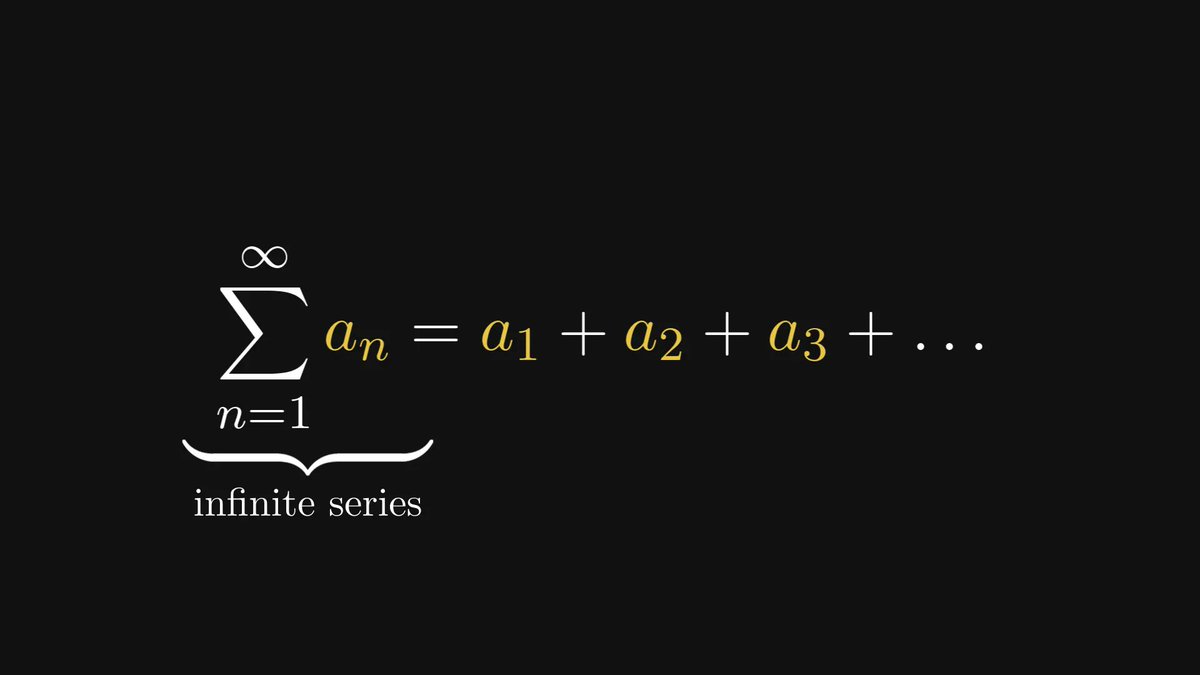In machine learning, we take gradient descent for granted.
We rarely question why it works.
What's usually told is the mountain-climbing analogue: to find the valley, step towards the steepest descent.
But why does this work so well? Read on.
We rarely question why it works.
What's usually told is the mountain-climbing analogue: to find the valley, step towards the steepest descent.
But why does this work so well? Read on.

Our journey is leading through
• differentiation, as the rate of change,
• the basics of differential equations,
• and equilibrium states.
Buckle up! Deep dive into the beautiful world of dynamical systems incoming. (Full post link at the end.)
• differentiation, as the rate of change,
• the basics of differential equations,
• and equilibrium states.
Buckle up! Deep dive into the beautiful world of dynamical systems incoming. (Full post link at the end.)
First, let's talk about derivatives and their mechanical interpretation!
Suppose that the position of an object at time t is given by the function x(t), and for simplicity, assume that it is moving along a straight line — as the distance-time plot illustrates below.
Suppose that the position of an object at time t is given by the function x(t), and for simplicity, assume that it is moving along a straight line — as the distance-time plot illustrates below.

What do the difference quotients represent?
The average speed on a given interval!
(Recall that speed is the ratio of distance and time.)
The average speed on a given interval!
(Recall that speed is the ratio of distance and time.)

The average speed has a simple geometric interpretation.
If you replace the object's motion with a constant velocity motion moving at the average speed, you'll end up at the same place.
The average speed is just the slope of the line connecting the start and endpoints.
If you replace the object's motion with a constant velocity motion moving at the average speed, you'll end up at the same place.
The average speed is just the slope of the line connecting the start and endpoints.
By moving the endpoint closer and closer to the starting point, we obtain the speed at the exact time.
Thus, the derivative describes speed. Similarly, the second derivative describes acceleration.
How is this relevant for gradient descent? Enter dynamical systems.
Thus, the derivative describes speed. Similarly, the second derivative describes acceleration.
How is this relevant for gradient descent? Enter dynamical systems.

As it turns out, the trajectory of a moving object can be described by its derivatives!
This is Newton's second law of motion.
This is Newton's second law of motion.

Newton's second law describes mechanics in terms of ordinary differential equations, that is, equations involving derivatives whose solutions are functions.
For instance, this is the differential equation describing a swinging pendulum, as given by Newton's second law.
For instance, this is the differential equation describing a swinging pendulum, as given by Newton's second law.

The simplest possible example: exponential growth.
If x(t) is the size of a bacterial colony, x′(t) = x(t) describes unlimited growth.
Think about x′(t) as the rate at which the population grows: without limitations in space and nutrients, cells can replicate whenever possible.
If x(t) is the size of a bacterial colony, x′(t) = x(t) describes unlimited growth.
Think about x′(t) as the rate at which the population grows: without limitations in space and nutrients, cells can replicate whenever possible.

There are multiple solutions, each determined by the initial value x(0).
Here are some of them plotted below.
Here are some of them plotted below.

In general, differential equations are formulated as initial value problems, where we are given
1) a differential equation,
2) and an initial value.
1) a differential equation,
2) and an initial value.

For instance, with the choice f(x) = x (1 - x), we obtain the famous logistic equation.
This models the population growth under a resource constraint.
If we assume that 1 is the capacity of our population, growth becomes more difficult as the size approaches this limit.
This models the population growth under a resource constraint.
If we assume that 1 is the capacity of our population, growth becomes more difficult as the size approaches this limit.

Here comes the essential part: by studying the sign of f(x) = x (1 - x), we can describe the behavior of solutions! Why?
Because f(x(t)) determines x'(t), and the sign of the derivative x'(t) determines the monotonicity of the solution x(t).
Because f(x(t)) determines x'(t), and the sign of the derivative x'(t) determines the monotonicity of the solution x(t).

This is visualized by the so-called phase portrait.
(The arrows on the x-axis indicate the direction of the solutions' flow.)
(The arrows on the x-axis indicate the direction of the solutions' flow.)

There are two very special solutions: the constant functions x(t) = 0 and x(t) = 1.
These are called equilibrium points/solutions, and they are determined by the zeroes of f(x).
These are called equilibrium points/solutions, and they are determined by the zeroes of f(x).

Why are these important?
Because the so-called stable equilibrium points attract the nearby solutions.
Again, check the stable equilibrium x₀ = 1 in the case of the logistic equation.
Because the so-called stable equilibrium points attract the nearby solutions.
Again, check the stable equilibrium x₀ = 1 in the case of the logistic equation.

Let's talk about finding the solutions.
As differential equations are often not possible to solve explicitly, we resort to numerical methods.
The simplest one is replacing the derivative with finite differences to discretize the solution.
As differential equations are often not possible to solve explicitly, we resort to numerical methods.
The simplest one is replacing the derivative with finite differences to discretize the solution.

This means that if the step size h is small enough, the function f and the initial value x(0) can be used to approximate x(h). 

Thus, by defining the recursive sequence below, we obtain a discretized solution.
This is called Euler's method.
This is called Euler's method.

The smaller the step size, the better the approximation.
Here are some of the discretized solutions for the logistic equation.
Here are some of the discretized solutions for the logistic equation.

If the discretized solution looks familiar, it's not an accident.
If f is the derivative of some F, then this is gradient ascent, the algorithm that is used to maximize F.
In the case of the logistic equation, F takes the form of a simple third-degree polynomial.
If f is the derivative of some F, then this is gradient ascent, the algorithm that is used to maximize F.
In the case of the logistic equation, F takes the form of a simple third-degree polynomial.

We can easily obtain gradient descent: by maximizing -F, we minimize F.
Thus, gradient descent works because dynamical systems move towards stable equilibria.
(Of course, there are lots of nuances here, but this is the general idea.)
Thus, gradient descent works because dynamical systems move towards stable equilibria.
(Of course, there are lots of nuances here, but this is the general idea.)
I have published an extensive 2500+ word post about this topic, so check it out for detailed explanations.
Read the full post here (and subscribe to get more posts like this one every week):
thepalindrome.org/p/why-does-gra…
Read the full post here (and subscribe to get more posts like this one every week):
thepalindrome.org/p/why-does-gra…
This is also a part of my Mathematics of Machine Learning book.
Tons of intuitive explanations and hands-on examples, all with a focus on machine learning.
Get it here: amazon.com/Mathematics-Ma…
Tons of intuitive explanations and hands-on examples, all with a focus on machine learning.
Get it here: amazon.com/Mathematics-Ma…
If you have enjoyed this thread, share it with your friends, follow me, and subscribe to my newsletter!
Understanding mathematics is a superpower. I'll help you get there, step by step.
thepalindrome.org
Understanding mathematics is a superpower. I'll help you get there, step by step.
thepalindrome.org
• • •
Missing some Tweet in this thread? You can try to
force a refresh