Thread by @TivadarDanka

What you see below is one of the most beautiful formulas in mathematics.

A single equation, establishing a relation between 𝑒, π, the imaginary number, and 1. It is mind-blowing.

This is what's behind the sorcery:

First, let's go back to square one: differentiation.

The derivative of a function at a given point describes the slope of its tangent plane.

By definition, the derivative is the limit of difference quotients: slopes of line segments that get closer and closer to the tangent.

These quantities are called "difference quotients".

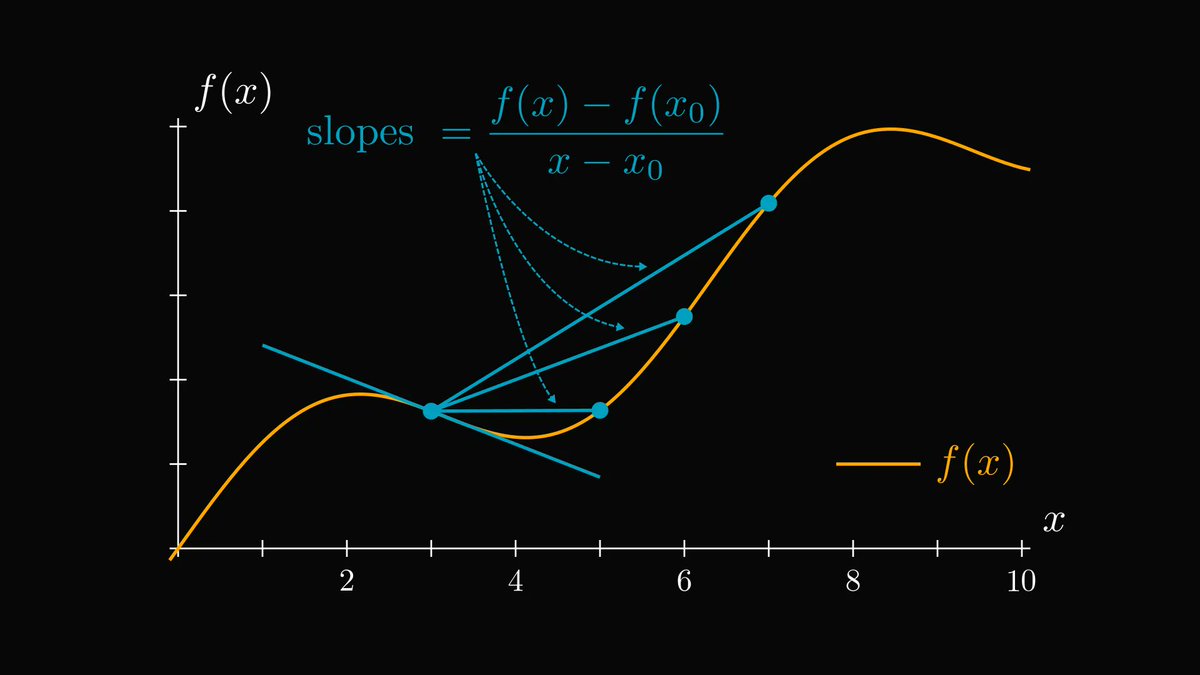
Here is the precise definition of the derivative.

Take a mental note, as this is going to be essential.

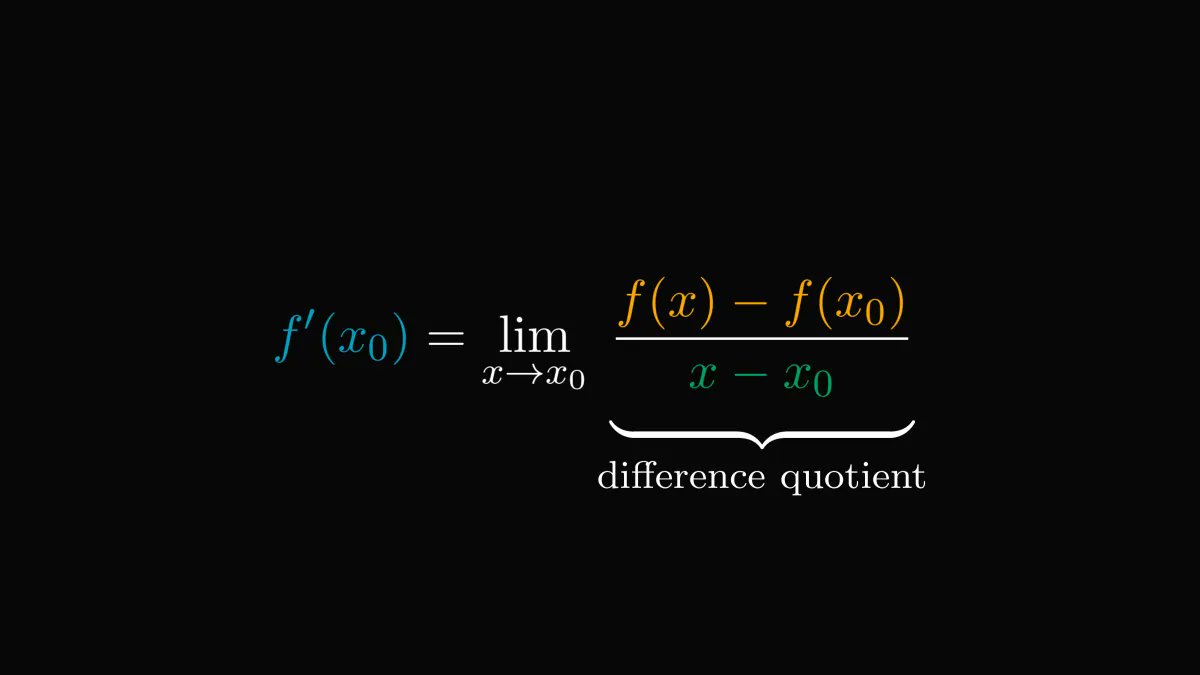
Due to what limits are, we can write the derivative as the difference quotient plus a small error term.

This is a minor but essential change in our viewpoint.

By rearranging the terms, we see that a differentiable function equals a linear part + error.

In essence, differentiation is the same as a linear approximation.

I am not going to lie: this is mindblowing.

If you don't believe me, check out this plot.

Around x₀, the linear function given by the derivative is pretty close to our function.

In fact, this is the best possible local linear approximation.

If the linear approximation is not good enough, can we do better?

Sure. For instance, the first and second derivatives give the best local quadratic approximation.

You guessed right. The first n derivatives determine the best local approximation by an n-th degree polynomial.

This is the n-th Taylor polynomial of f around x₀.

For instance, this is what the Taylor polynomials around zero look like for sin(x).

As you can see, higher-order Taylor polynomials are almost indistinguishable from sin(x).

This is not an accident.

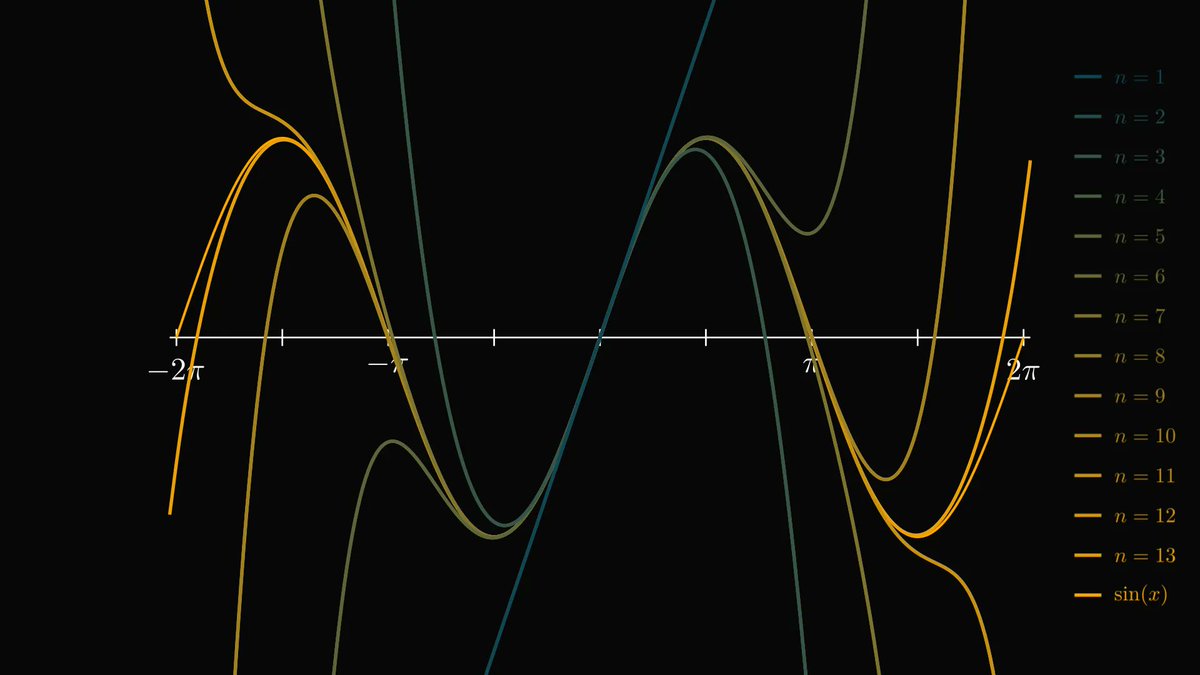
Hold on to your seats: if you think big and let n to infinity, the resulting Taylor expansion can yield the original function!

(Functions where this is true are called analytic, but the terminology is not important for us.)

For example, this holds for our favorite trigonometric functions, sine and cosine.

(You can verify this by hand using the derivatives of sine and cosine.)

The Taylor expansion of the amazing exponential function also yields itself.

This is one of the most important formulas in mathematics.

Why?

Because we can use it to extend the exponential function onto the complex plane!

(I don't want to scare you, but you can even plug in matrices. We'll stick to complex numbers, though.)

Now, by letting z = i x, we stumble upon something staggering.

The complex exponential function is a linear combination of trigonometric functions!

The first time I learned about this, my head exploded.

This is Euler's formula in its full might.

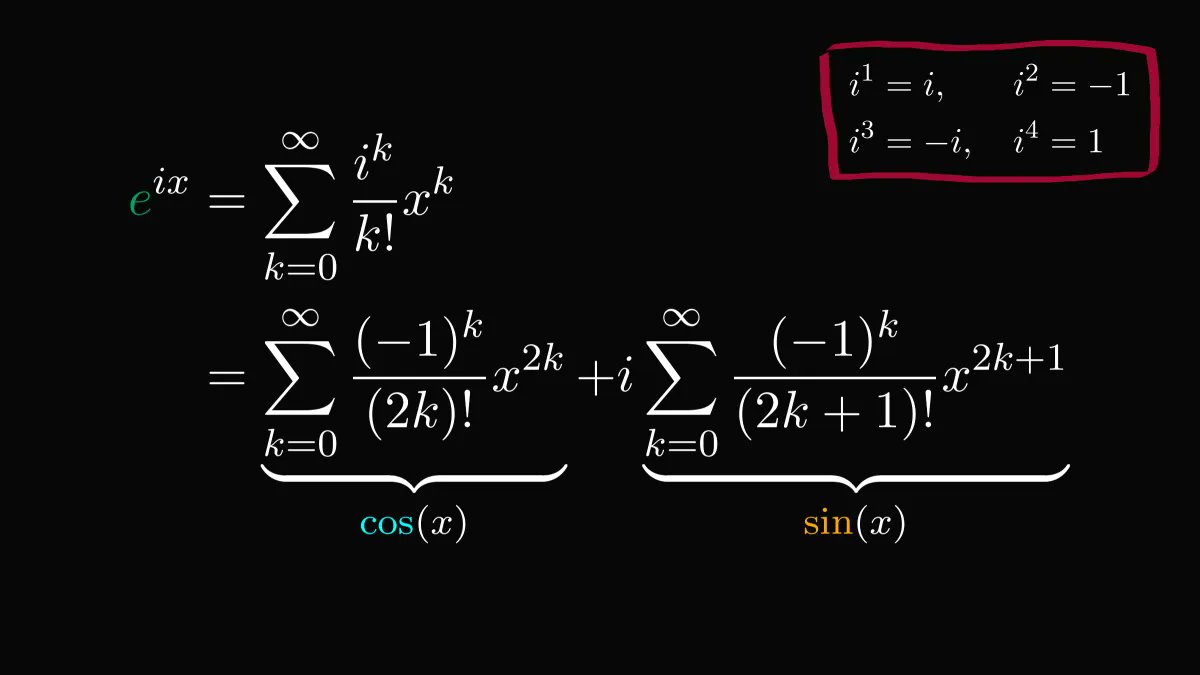
By plugging in π, we get the famous Euler's identity.

This result wins almost all "what's the most beautiful formula of mathematics" contests.

Besides its staggering beauty, there is much more to it.

Euler's formula connects the polar form of complex numbers with the exponential function.

This fundamental identity underlies the entire field of science and engineering.

(This is how the polar form is visualized on the complex plane.)

If you have enjoyed this explanation, there is more in my Mathematics of Machine Learning book.

Understanding mathematics will make you a better engineer, and I want to help you with that.

Get the book here: amazon.com/Mathematics-Ma…