Problem-solving is at least 50% of every job in tech and science.
Mastering problem-solving will make your technical skill level shoot up like a hockey stick. Yet, we are rarely taught how to do so.
Here are my favorite techniques that'll loosen even the most complex knots:
Mastering problem-solving will make your technical skill level shoot up like a hockey stick. Yet, we are rarely taught how to do so.
Here are my favorite techniques that'll loosen even the most complex knots:

0. Is the problem solved yet?
The simplest way to solve a problem is to look for the solution elsewhere. This is not cheating; this is pragmatism. (Except if it is a practice problem. Then, it is cheating.)
The simplest way to solve a problem is to look for the solution elsewhere. This is not cheating; this is pragmatism. (Except if it is a practice problem. Then, it is cheating.)
When your objective is to move fast, this should be the first thing you attempt.
This is the reason why Stack Overflow (and its likes) are the best friends of every programmer.
This is the reason why Stack Overflow (and its likes) are the best friends of every programmer.
1. Is there an analogous problem?
If A is analogous to B, and A plays a role in your problem, swapping them might reveal an insight into your problem.
An example: circles and spheres are analogous, as they are the same objects in different dimensions.
If A is analogous to B, and A plays a role in your problem, swapping them might reveal an insight into your problem.
An example: circles and spheres are analogous, as they are the same objects in different dimensions.

Thus, if you are facing a geometric problem that involves spheres, bumping it down a dimension can highlight a simpler solution that can be mapped to the source problem.
Quoting Stefan Banach (the inventor of functional analysis), "A mathematician is a person who can find analogies between theorems; a better mathematician is one who can see analogies between proofs and the best mathematician can notice analogies between theories."
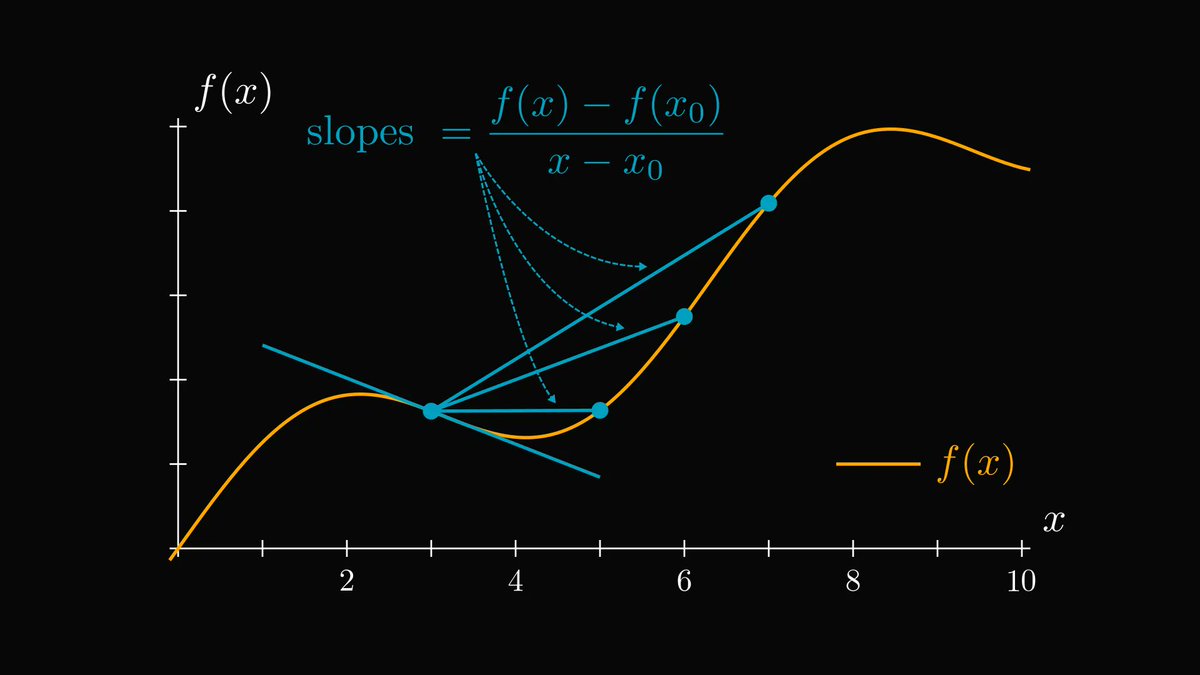
2. Wishful thinking.
Sometimes, the best thing to do is pretend the solution exists and move forward.
I’ll illustrate this with a mathematical example. Let’s talk about the Singular Value Decomposition (SVD).
Sometimes, the best thing to do is pretend the solution exists and move forward.
I’ll illustrate this with a mathematical example. Let’s talk about the Singular Value Decomposition (SVD).
This famous result states that every real matrix A can be decomposed into a product of an
1. orthogonal matrix U (that is, UUᵀ is the identity matrix),
2. a diagonal matrix Σ,
3. and another orthogonal matrix Vᵀ.
We find them via wishful thinking: we pretend that they exist.
1. orthogonal matrix U (that is, UUᵀ is the identity matrix),
2. a diagonal matrix Σ,
3. and another orthogonal matrix Vᵀ.
We find them via wishful thinking: we pretend that they exist.

If they do, then AAᵀ, which is a real symmetric matrix, equals to AAᵀ = UΣ²Uᵀ. This U can be found via the spectral decomposition theorem! We can find V similarly.
We found U and V by pretending they exist.
We found U and V by pretending they exist.

3. Can you solve a special case?
Reducing the problem to a special case is also an extremely powerful technique. The previously shown SVD was solved by reducing the general case to the real symmetric case.
Reducing the problem to a special case is also an extremely powerful technique. The previously shown SVD was solved by reducing the general case to the real symmetric case.

4. Is this a special case of a general problem?
This is the counterpart of the previous case and can be similarly powerful.
For instance, consider this geometric shape. Is there a vertical cut that cuts this into two parts of equal area?
This is the counterpart of the previous case and can be similarly powerful.
For instance, consider this geometric shape. Is there a vertical cut that cuts this into two parts of equal area?

Our first instinct is to start calculating its area up to a cutoff, but this is extremely complicated.
All we have to notice is that the area given the position of the vertical slice is a continuous function.
All we have to notice is that the area given the position of the vertical slice is a continuous function.

As f(0) = 0, f(1) = area, and f is continuous, it has to cross area/2.
This is a general result, and our problem is a special case of this. It doesn’t matter what f is exactly.
Much simpler than solving equations involving inverse trigonometric functions.
This is a general result, and our problem is a special case of this. It doesn’t matter what f is exactly.
Much simpler than solving equations involving inverse trigonometric functions.

5. Can you draw a picture?
Our thinking is more visual than formal, and solving problems is much easier visually too.
The simplest example is probably the De Morgan identities: they are trivial to see visually, but more difficult to prove formally.
Our thinking is more visual than formal, and solving problems is much easier visually too.
The simplest example is probably the De Morgan identities: they are trivial to see visually, but more difficult to prove formally.

6. Is there a simpler approach?
Our first ideas are often vastly overcomplicated, taking us down a rabbit hole we don't need to go.
For example, I have posted a simple puzzle a few years ago about poles and cables. Here it is:
Our first ideas are often vastly overcomplicated, taking us down a rabbit hole we don't need to go.
For example, I have posted a simple puzzle a few years ago about poles and cables. Here it is:

The first idea is to use catenary curves and calculus, but there is a simple solution: as the cables hang 10 m above ground, they drop 40 m from the top of the pole. Hence, the distance between the two poles must be 0 m.
Simplifying our approach is always beneficial.
Simplifying our approach is always beneficial.
If you liked this thread, you will love The Palindrome, my weekly newsletter on Mathematics and Machine Learning.
Join 18000+ curious readers here: thepalindrome.org
Join 18000+ curious readers here: thepalindrome.org
• • •
Missing some Tweet in this thread? You can try to
force a refresh