Thread by @TivadarDanka

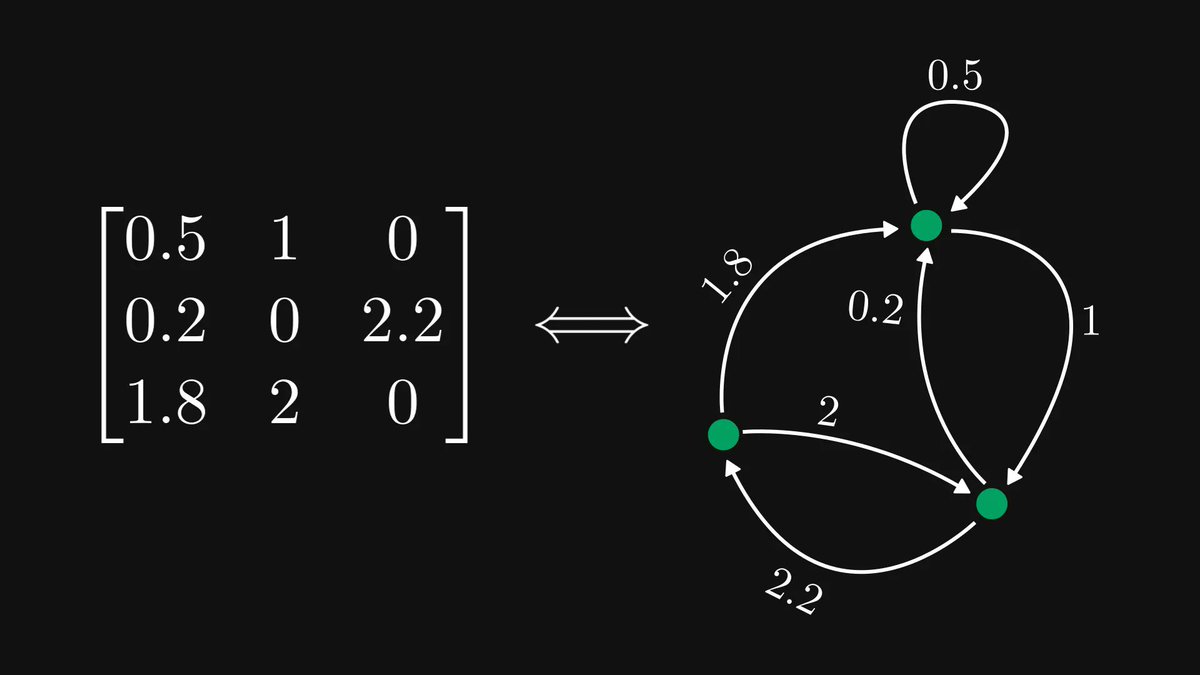
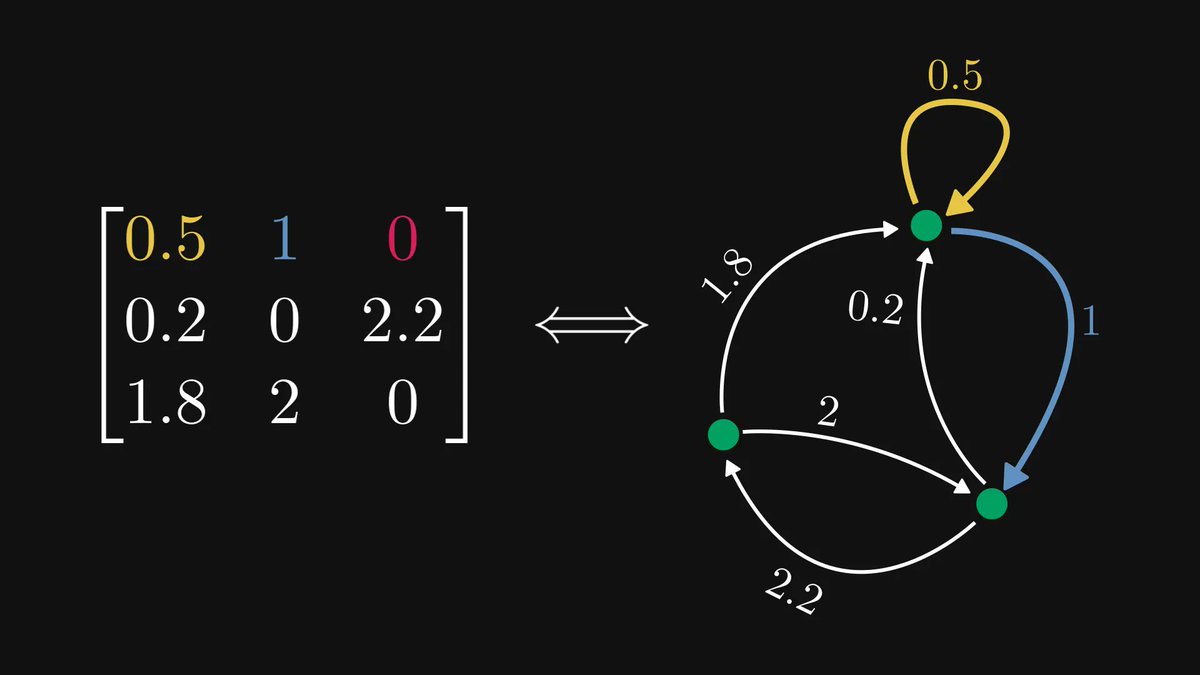
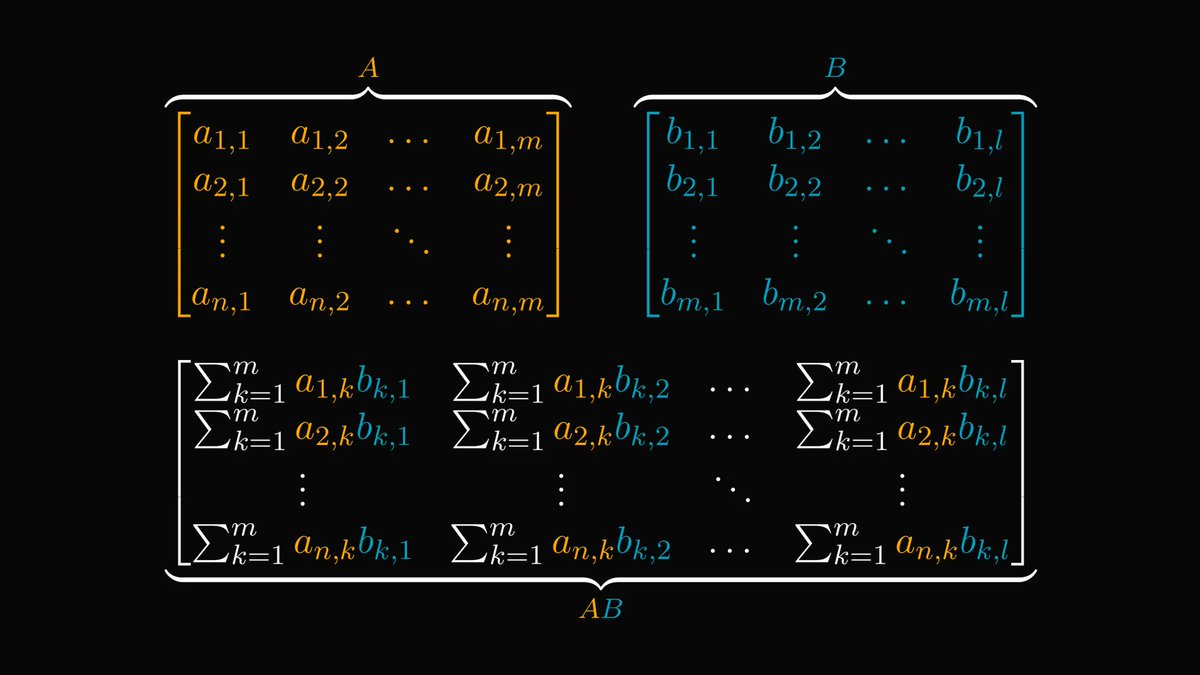
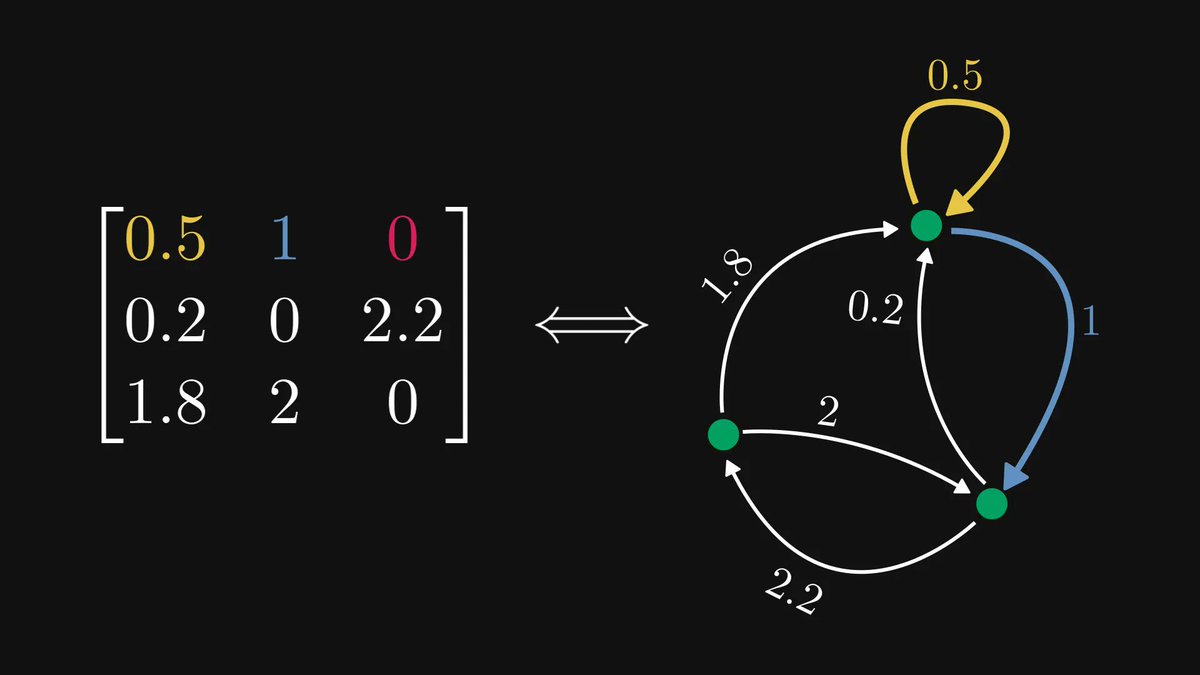
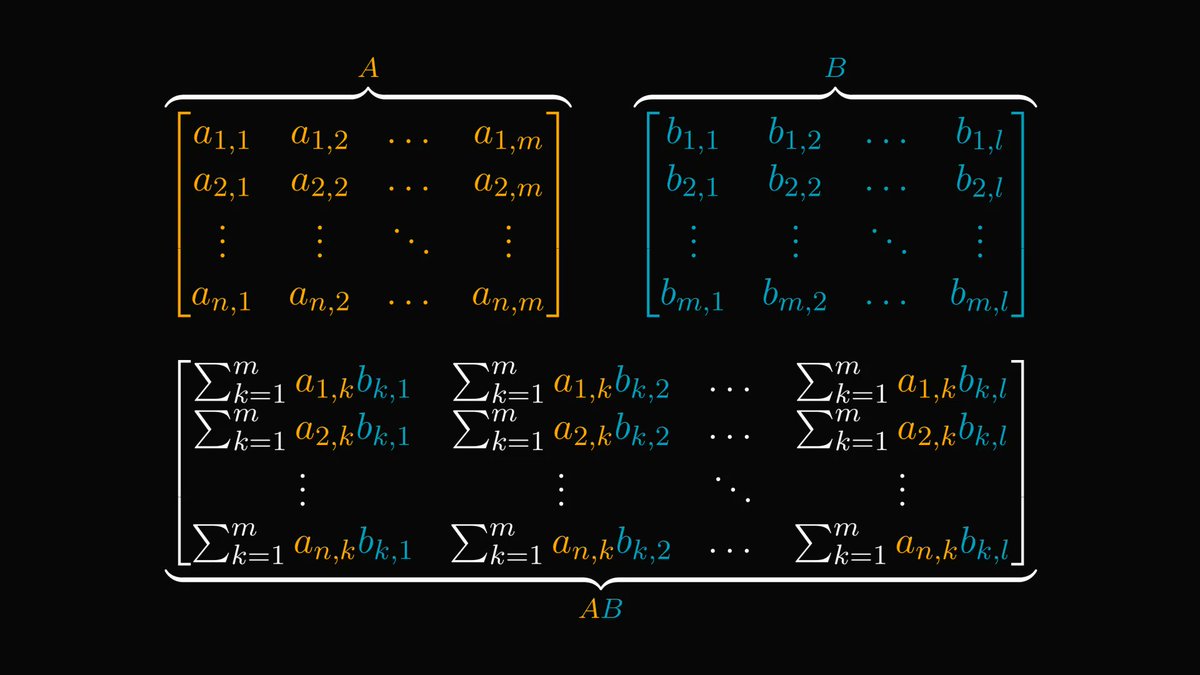
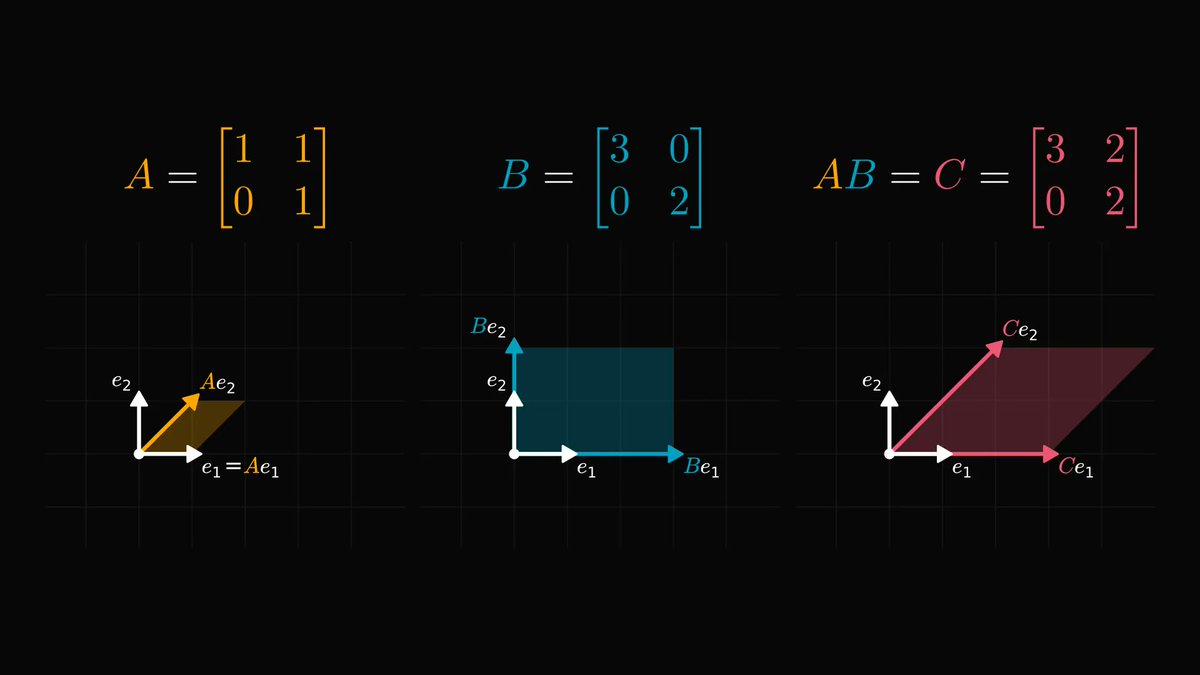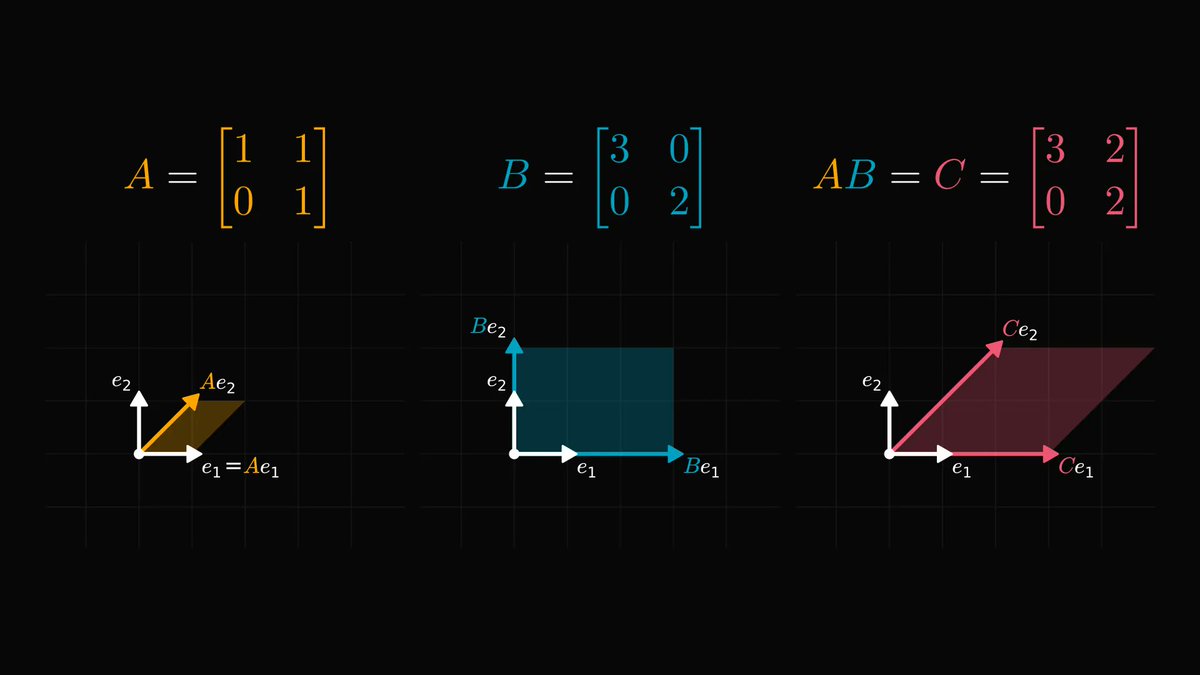In calculus, going from a single variable to millions of variables is hard.

Understanding the three main types of functions helps make sense of multivariable calculus.

Surprisingly, they share a deep connection. Let's see why!

In general, a function assigns elements of one set to another.

This is too abstract for most engineering applications. Let's zoom in a little!

As our measurements are often real numbers, we prefer functions that operate on real vectors or scalars.

There are three categories:

1. vector-scalar,
2. vector-vector,
3. and scalar-vector.

When speaking about multivariable calculus, vector-scalar functions come to mind first.

Instead of a graph (like their single-variable counterparts), they define surfaces.

You can think about a vector-scalar function as a topographic map.

(Image source: Wikipedia, ) en.wikipedia.org/wiki/Terrain_c…

Although often not denoted, the argument of a vector-scalar function is always a vector.

Most frequently, we write out the components - a.k.a. the variables - explicitly.

Want a practical example of a vector-scalar function?

The loss of a predictive model maps the vector of parameters to a single scalar.

Below, you can see the mean-squared error of a simple linear regression model.

Next up, we have the vector-vector functions.

You can imagine them as a force field, putting a vector to each point.

The most important example of vector-vector functions is the gradient.

We call this a gradient field.

Let's visualize an example!

This is how the vector field given by the gradient of f(x, y) = x² + y² looks.

It is important to note that not all vector-vector functions are gradient fields!

For instance, f(x, y) = (x - xy, xy - y) cannot be a gradient.

Can you figure out the reason why? (Hint: take a look at the partial derivatives of f(x, y).)

Next up, we have scalar-vector functions, that is, curves.

Think about the scalar-vector function f(t) as the trajectory of a particle at time t.

Technically, there is only a single variable involved. Yet, curves play an essential role in multivariable calculus.

Remember how vector-vector functions define force fields?

Scalar-vector functions describe the trajectories of particles moving through them.

Gradient descent connects all of this.

In essence, gradient descent

1. takes the surface of the loss function,
2. computes the vector field given by the gradient,
3. and finds the trajectories given by the gradient vector field by a discrete approximation.

This is just the tip of the iceberg.

Multivariable calculus is one of the most powerful tools in machine learning, helping us to optimize functions in millions of variables.

That is quite a feat.

This explanation is directly from my new Mathematics of Machine Learning book.

I have packed 20 years of math studies into 700 pages full of intuitive and application-oriented lessons, the ultimate learning resource for you.

Get it now: amazon.com/Mathematics-Ma…