Thread by @TivadarDanka

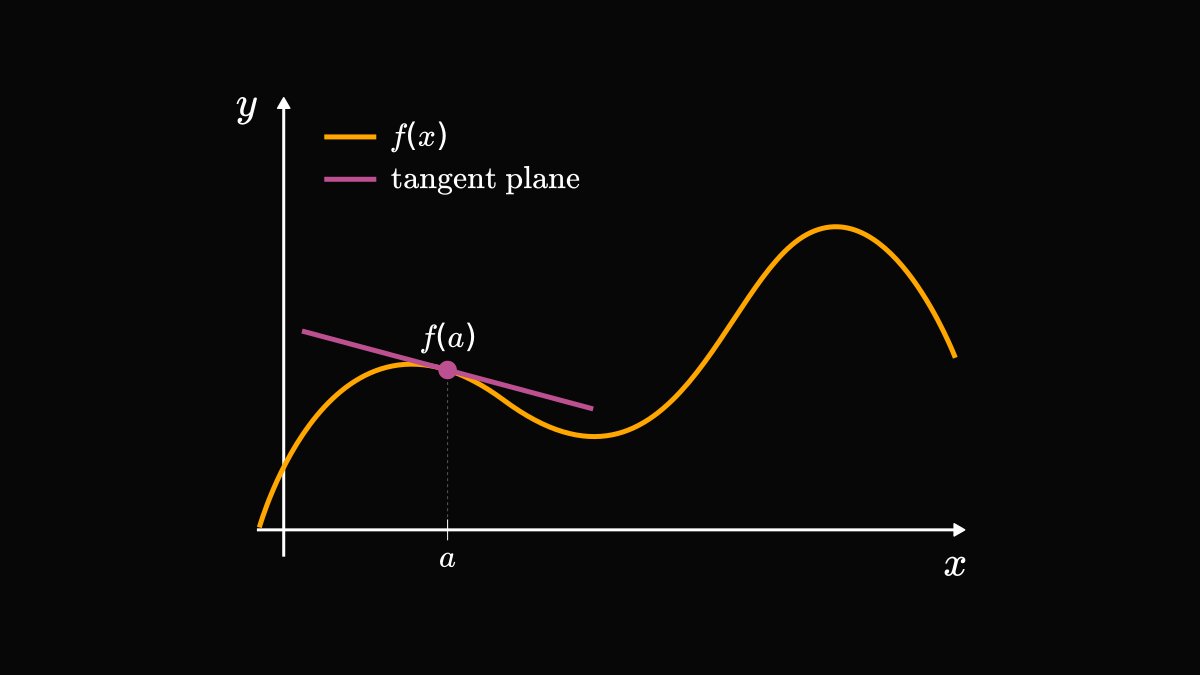
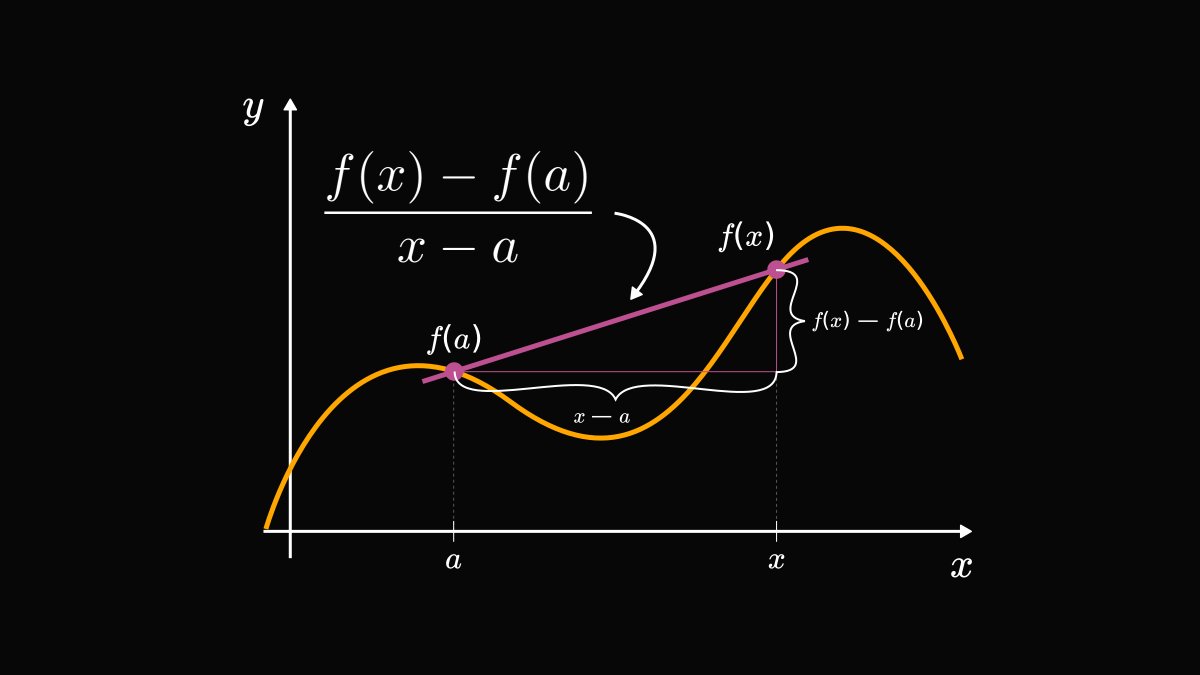
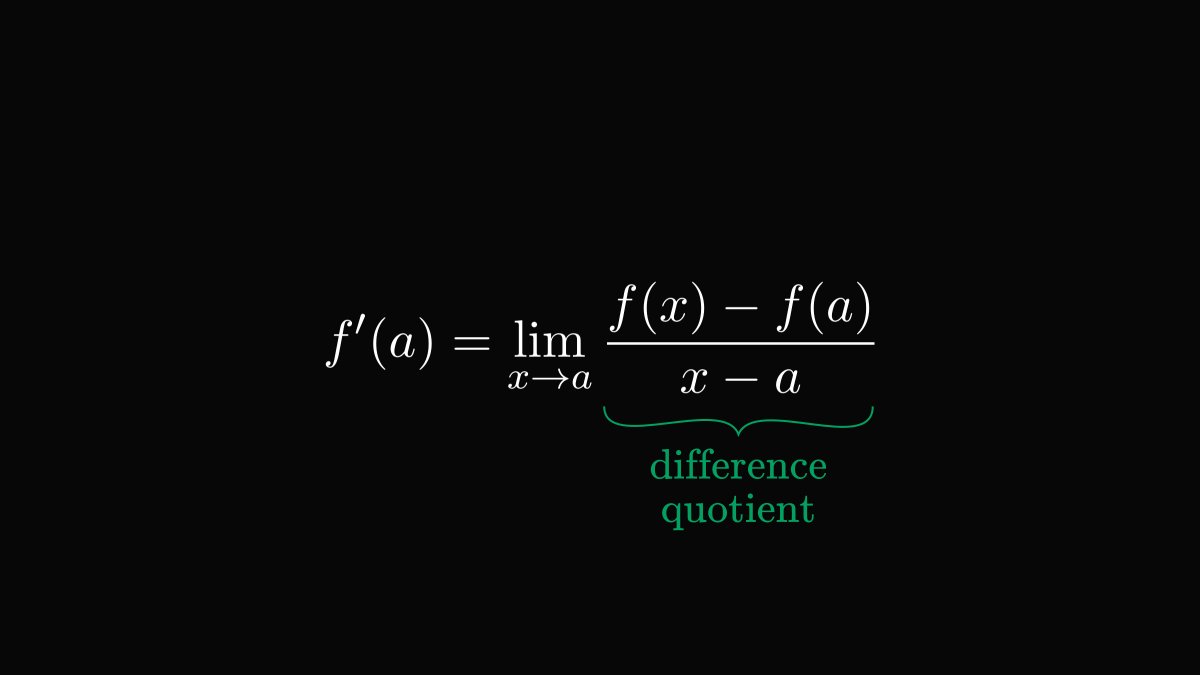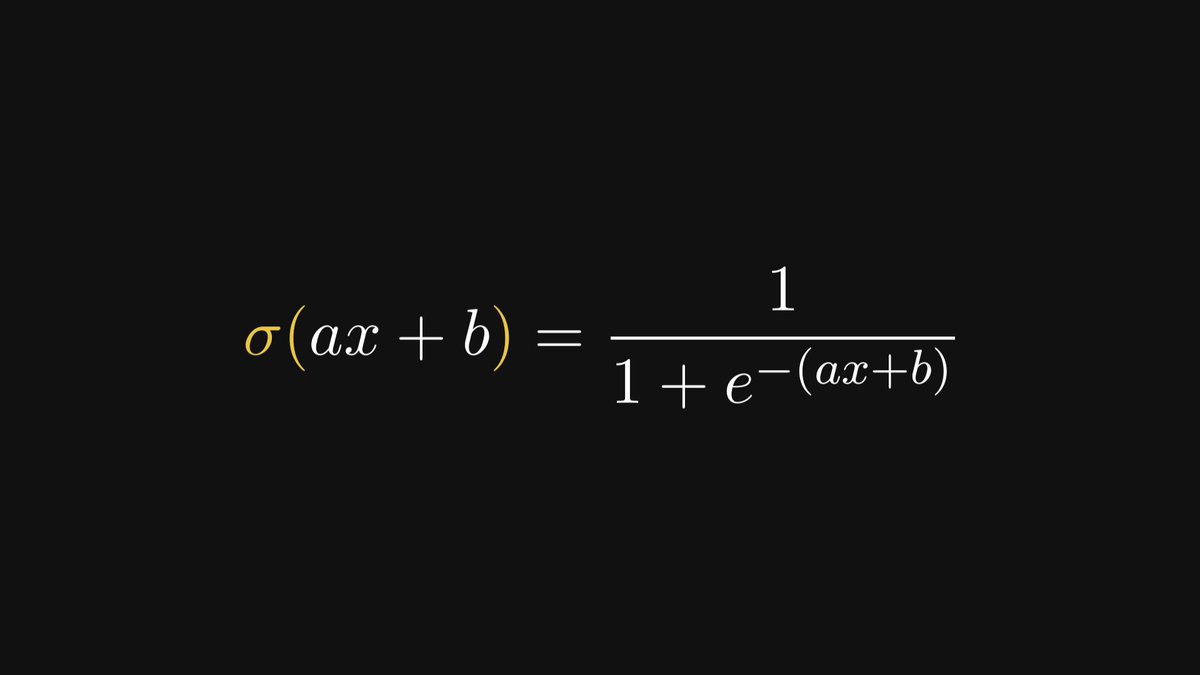Conditional probability is the single most important concept in statistics.

Why? Because without accounting for prior information, predictive models are useless.

Here is what conditional probability is, and why it is essential:

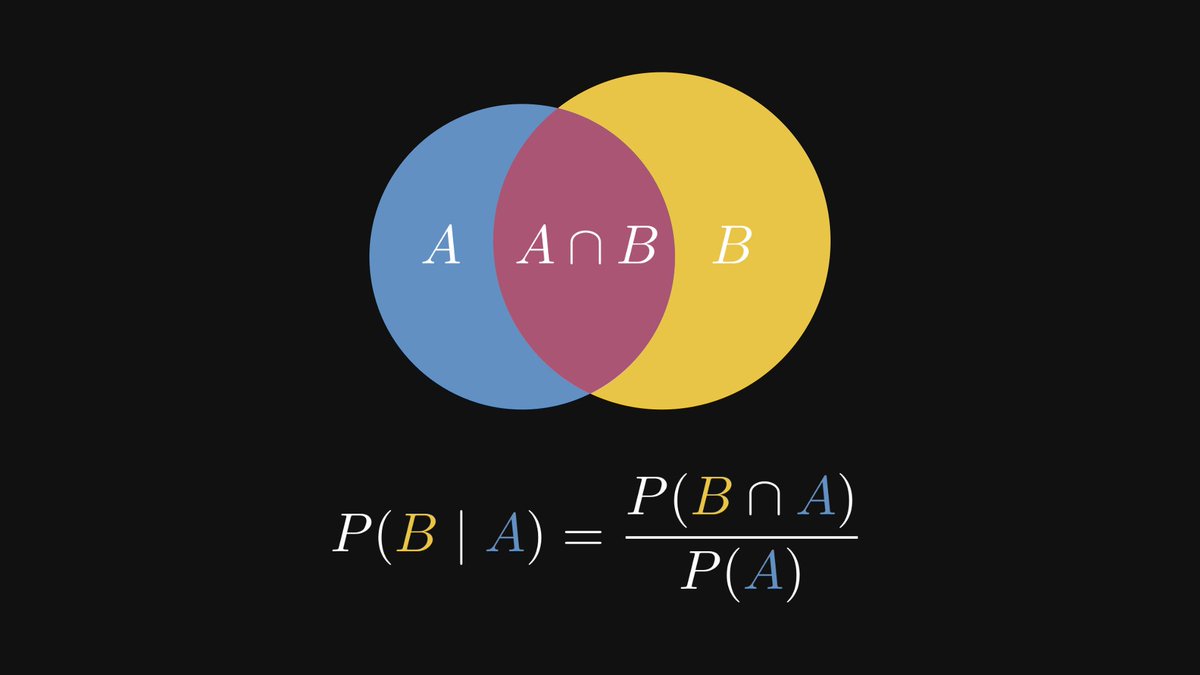
Conditional probability allows us to update our models by incorporating new observations.

By definition, P(B | A) describes the probability of an event B, given that A has occurred.

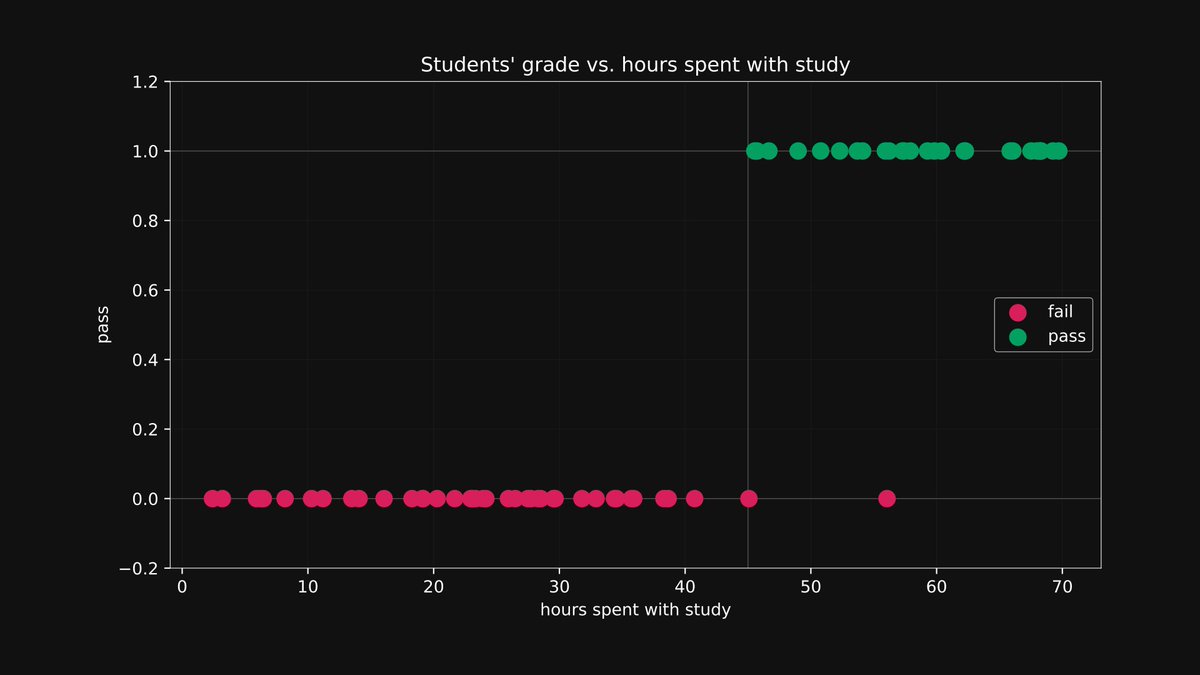
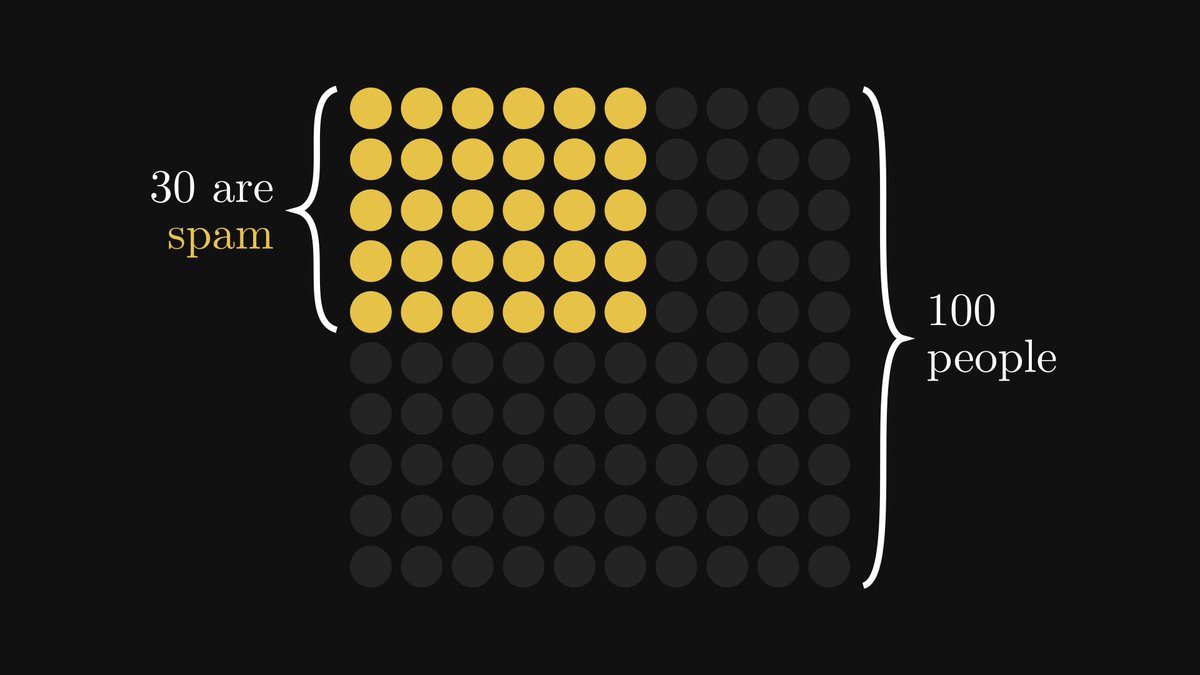
Here is an example. Suppose that among 100 emails, 30 are spam.

Based only on this information, if we inspect a random email, our best guess is a 30% chance of it being spam.

This is not good enough.

We can build a better model by looking at more information.

What about looking for certain keywords, like "deal"?

It turns out that among the 100 emails, 40 contain this word.

Let's say that an email contains the word "deal".

How does our probabilistic model change?

We can leverage the prior information to get a more precise prediction than the random 30%.

By taking a more detailed look, we notice that 24 emails with the word "deal" are spam.

Thus, we can compute the conditional probability by focusing on the mails containing "deal".

Using a similar logic, we get that without the expression "deal", the probability of spam drops to 10%!

Quite a difference between our model with no prior information.

Conditional probability restricts the event space, thus providing a more refined picture.

This gives better models, leading to better decisions.

Join 20,000+ ML practitioners who get 2 actionable emails every week to help them understand the math behind ML, make smarter decisions, and avoid costly mistakes.

Subscribe here (it’s free): thepalindrome.org