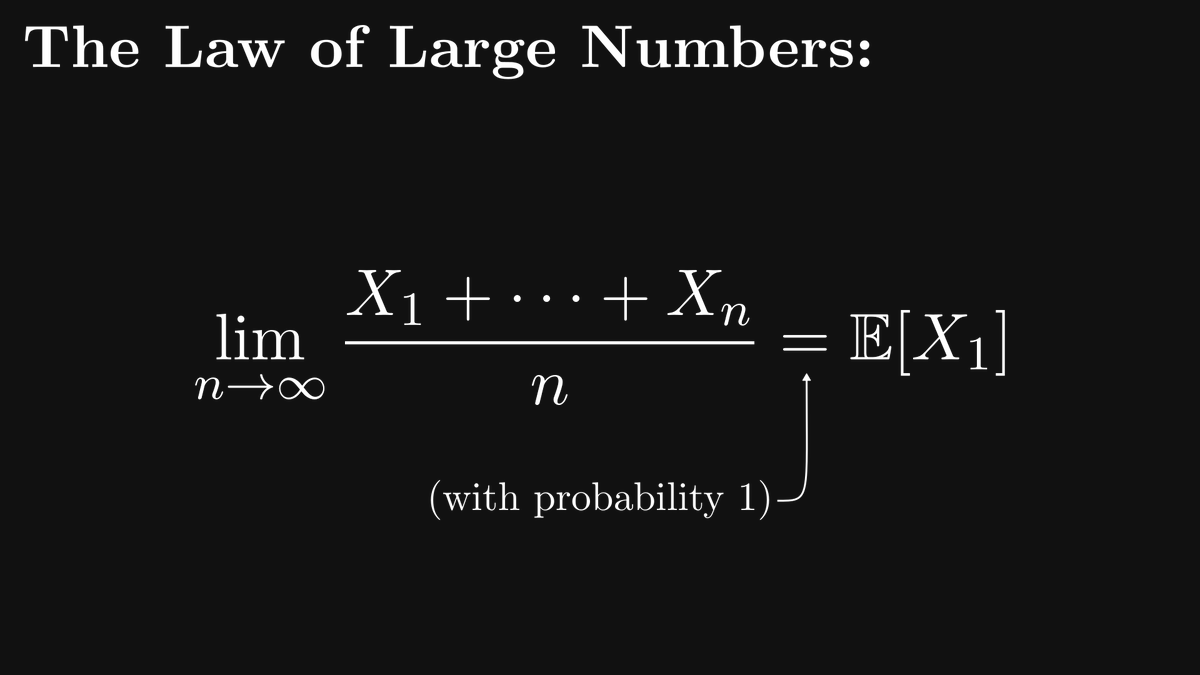There is a non-recursive formula for the Fibonacci numbers, expressing them in terms of the golden ratio and its powers.
Why should you be interested? Because it teaches an extremely valuable lesson about power series.
Read on to find out what:
Why should you be interested? Because it teaches an extremely valuable lesson about power series.
Read on to find out what:

The Fibonacci numbers form one of the most famous integer sequences, known for their intimate connection to the golden ratio, sunflower spirals, mating habits of rabbits, and several other things.
By definition, they are defined by a simple second-order recursion:
By definition, they are defined by a simple second-order recursion:

What’s usually not known is that the Fibonacci numbers have a simple and beautiful closed-form expression, written in terms of the golden ratio.
This is called the Binet formula.
In this thread, we are going to derive it from the first principles.
This is called the Binet formula.
In this thread, we are going to derive it from the first principles.
Let's start with our primary tool: power series.
A power series is an infinite sum of monomials. You can think about them as “polynomials of infinite degree”.
The coefficients of the monomials are called the coefficients of the power series.
A power series is an infinite sum of monomials. You can think about them as “polynomials of infinite degree”.
The coefficients of the monomials are called the coefficients of the power series.

One of the most important examples is the famous geometric series.
We’ll use this to derive the closed formula for the Fibonacci numbers.
We’ll use this to derive the closed formula for the Fibonacci numbers.

A power series is fully determined by its coefficients: two power series are equal if and only if their coefficients are equal.
This is called the uniqueness property of power series.
This is called the uniqueness property of power series.

Power series are also linear in a sense.
That is, summing two power series is the same as summing their coefficients.
That is, summing two power series is the same as summing their coefficients.

What happens if we define a power series via the Fibonacci numbers?
Let’s find out.
This is called the Fibonacci generating function:
Let’s find out.
This is called the Fibonacci generating function:

First, we’ll use recursion to obtain a closed-form expression for F(x).
Do you recall how the Fibonacci numbers were initially defined?
We can multiply each term by the corresponding monomial to obtain the terms of the generating function on both sides.
Do you recall how the Fibonacci numbers were initially defined?
We can multiply each term by the corresponding monomial to obtain the terms of the generating function on both sides.

The right-hand side is a rational fraction, that is, the fraction of two polynomials.
How are we going to find the power series for this particular rational fraction?
By taking a closer look at the polynomial 1 - x - x² in the denominator.
How are we going to find the power series for this particular rational fraction?
By taking a closer look at the polynomial 1 - x - x² in the denominator.
The second-degree polynomial 1 - x - x² is a famous one. Why?
Let’s take a look at its roots via the quadratic formula:
Let’s take a look at its roots via the quadratic formula:

These two numbers are quite special.
Geometrically speaking, they describe the segments a and b such that the ratio of a to b is the same as a to a + b.
Geometrically speaking, they describe the segments a and b such that the ratio of a to b is the same as a to a + b.

Besides its geometric properties, the golden ratio and its conjugate are also special in an algebraic way.
Their sum and product are 1 and -1, respectively, while their difference is √5.
Their sum and product are 1 and -1, respectively, while their difference is √5.

Take note of these, as they’ll come in shortly.
What can we do with all of these? As the golden ratio and its conjugate are the roots of 1 - x - x², we can decompose this quadratic polynomial into the product of two linear terms.
How? Via the partial fraction decomposition.
What can we do with all of these? As the golden ratio and its conjugate are the roots of 1 - x - x², we can decompose this quadratic polynomial into the product of two linear terms.
How? Via the partial fraction decomposition.

We love rational fractions for one main reason: because they can be decomposed into the sum of geometric series.
In the case of the Fibonacci generating function, the decomposition is particularly simple.
In the case of the Fibonacci generating function, the decomposition is particularly simple.

Using the fact that two polynomials are equal if and only if their coefficients are equal leads to a simple system of linear equations. 

Applying this to the Fibonacci generating function, we can obtain its final form.
(Recall that addition and scalar multiplication of power series can be done coefficientwise.)
(Recall that addition and scalar multiplication of power series can be done coefficientwise.)

And thus, we finally obtain the Binet formula!
(As follows from the uniqueness property of power series.)
(As follows from the uniqueness property of power series.)

Most machine learning practitioners don’t understand the math behind their models.
That's why I've created a FREE roadmap so you can master the 3 main topics you'll ever need: algebra, calculus, and probabilities.
Get the roadmap here: thepalindrome.org/p/the-roadmap-…
That's why I've created a FREE roadmap so you can master the 3 main topics you'll ever need: algebra, calculus, and probabilities.
Get the roadmap here: thepalindrome.org/p/the-roadmap-…
• • •
Missing some Tweet in this thread? You can try to
force a refresh