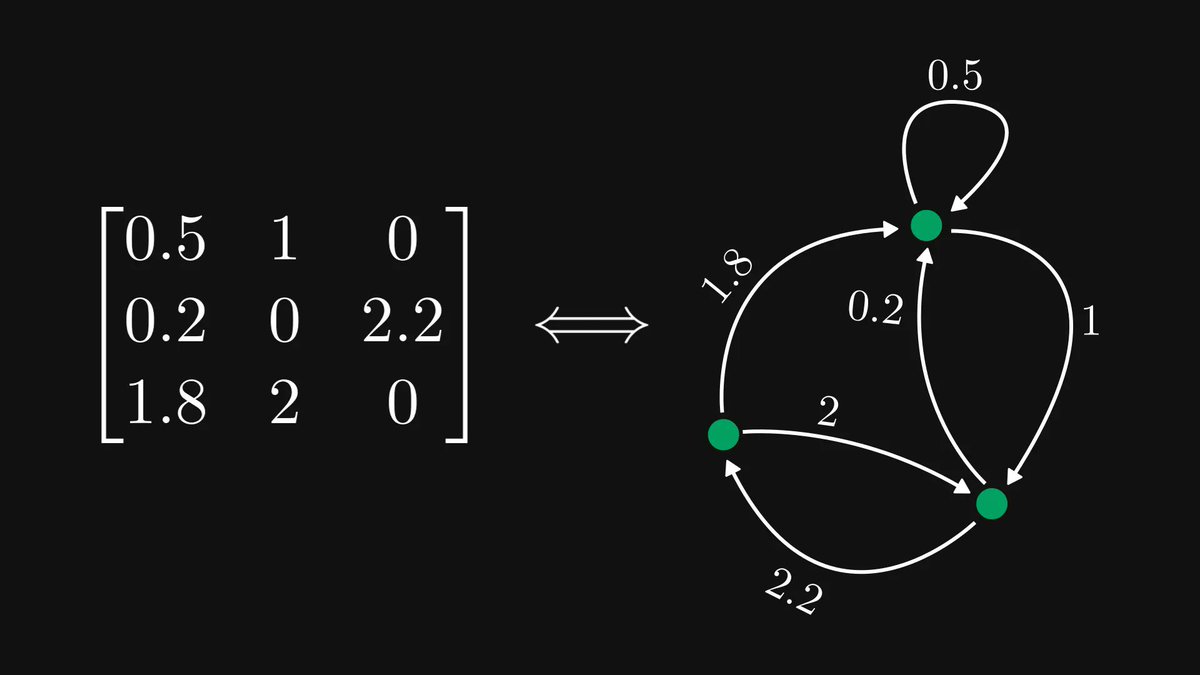
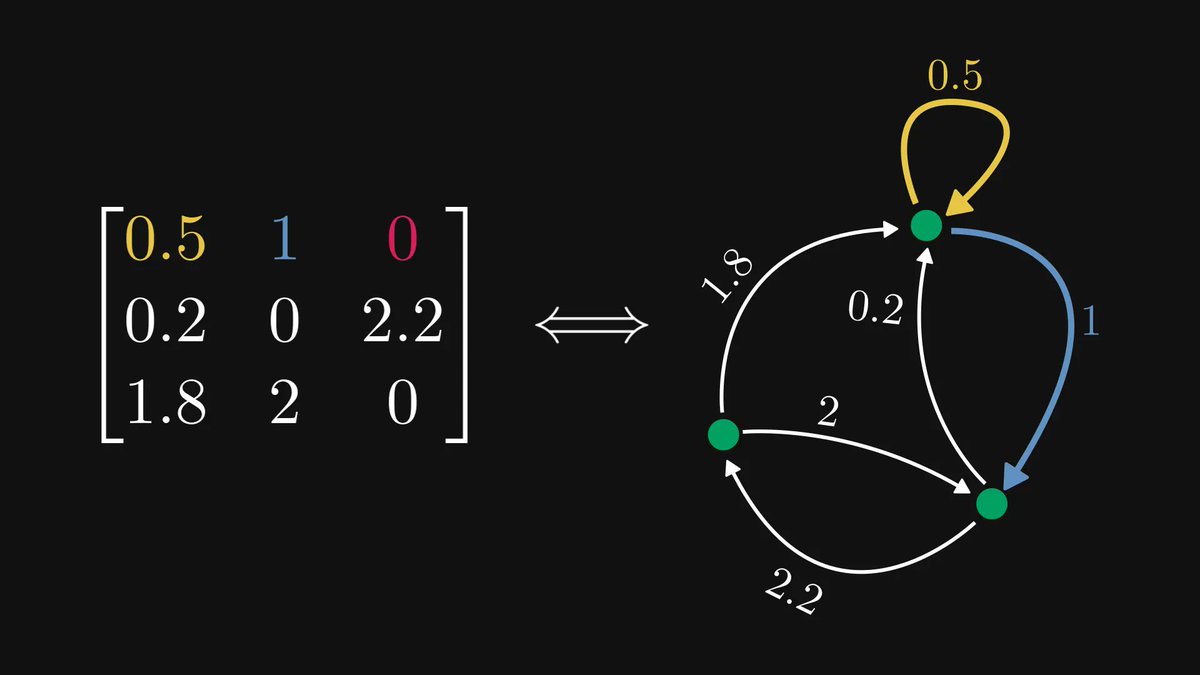
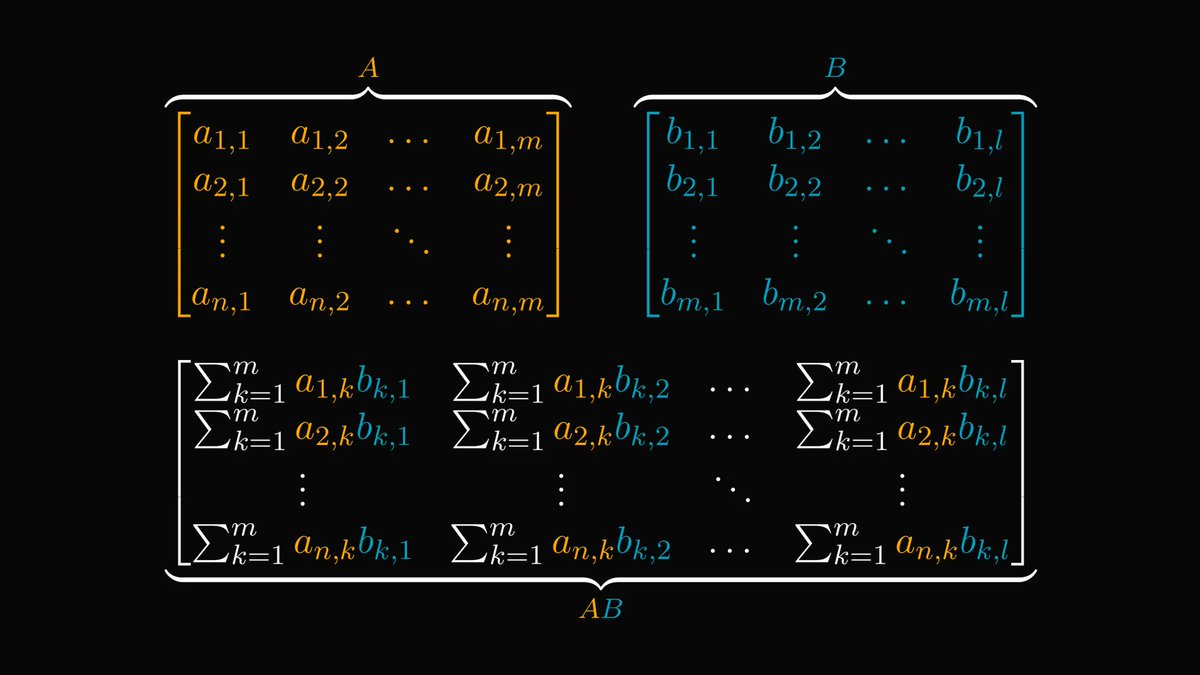
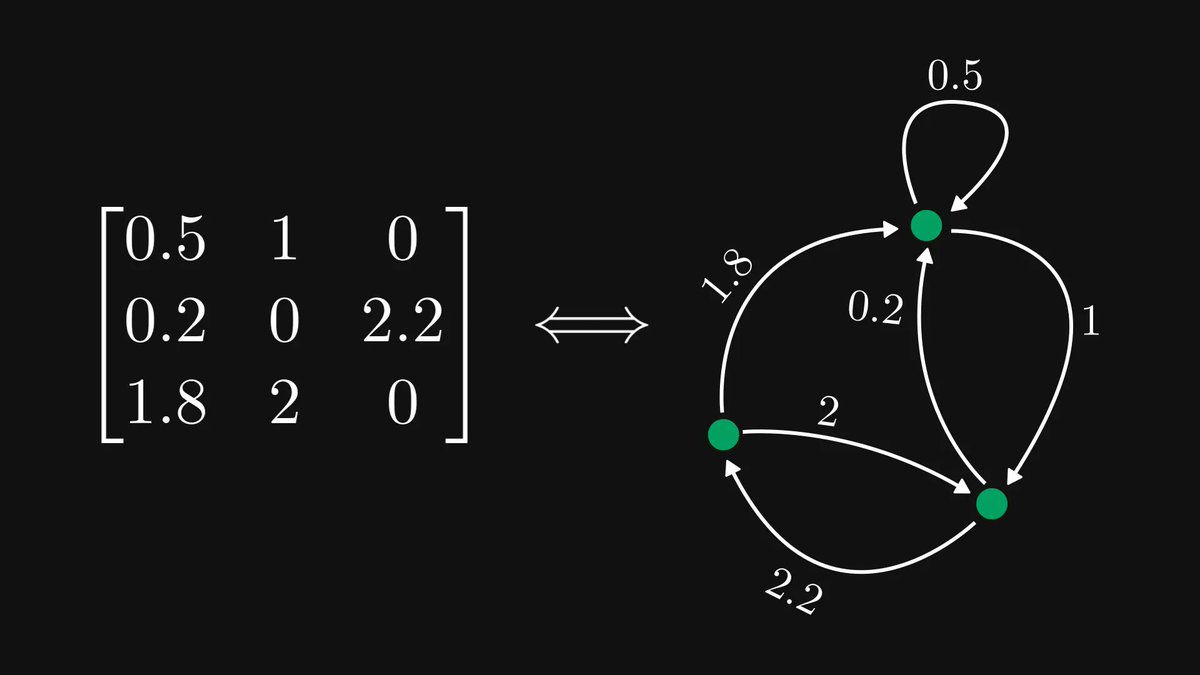
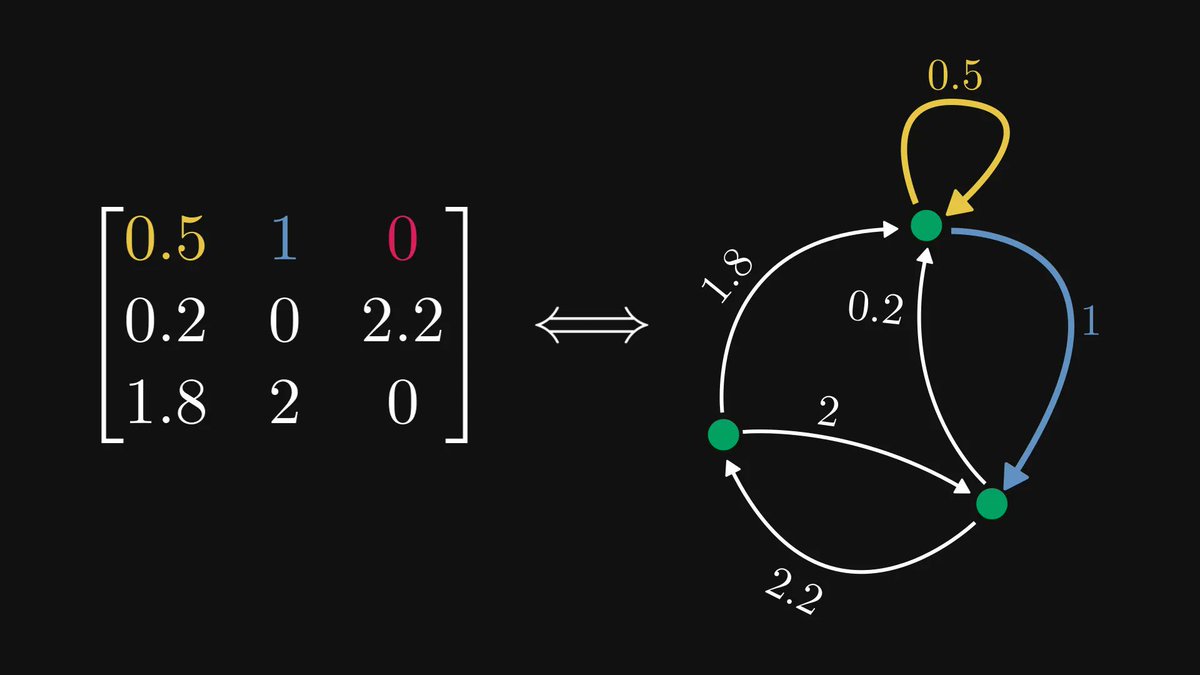
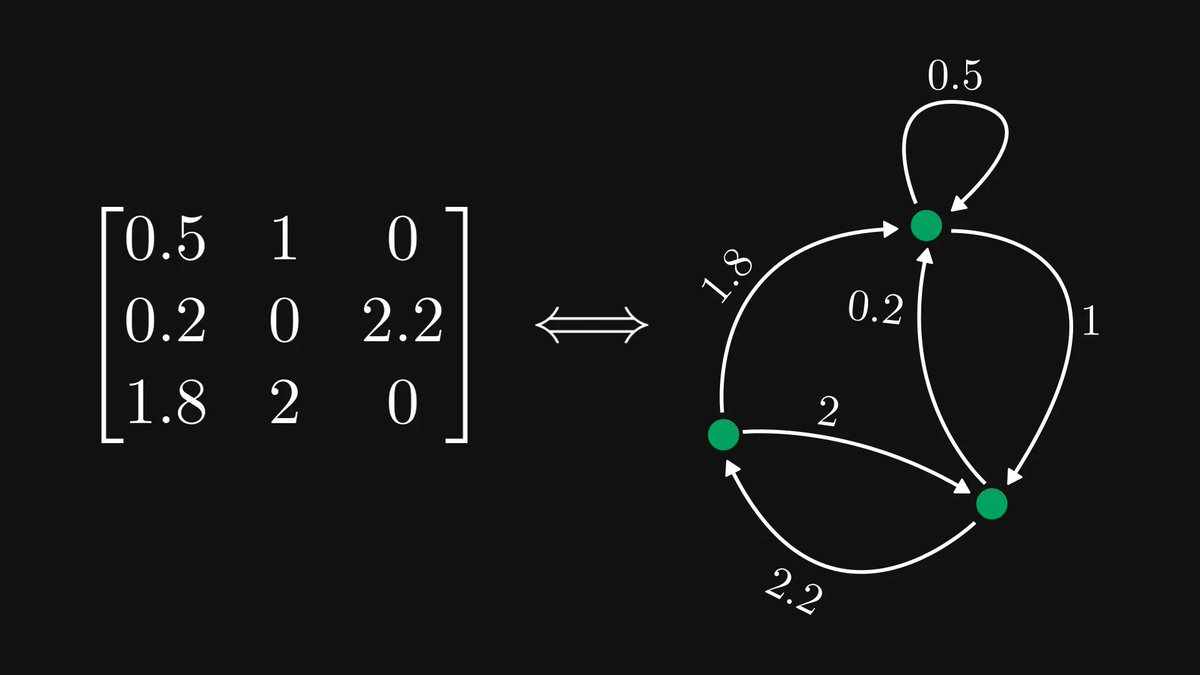
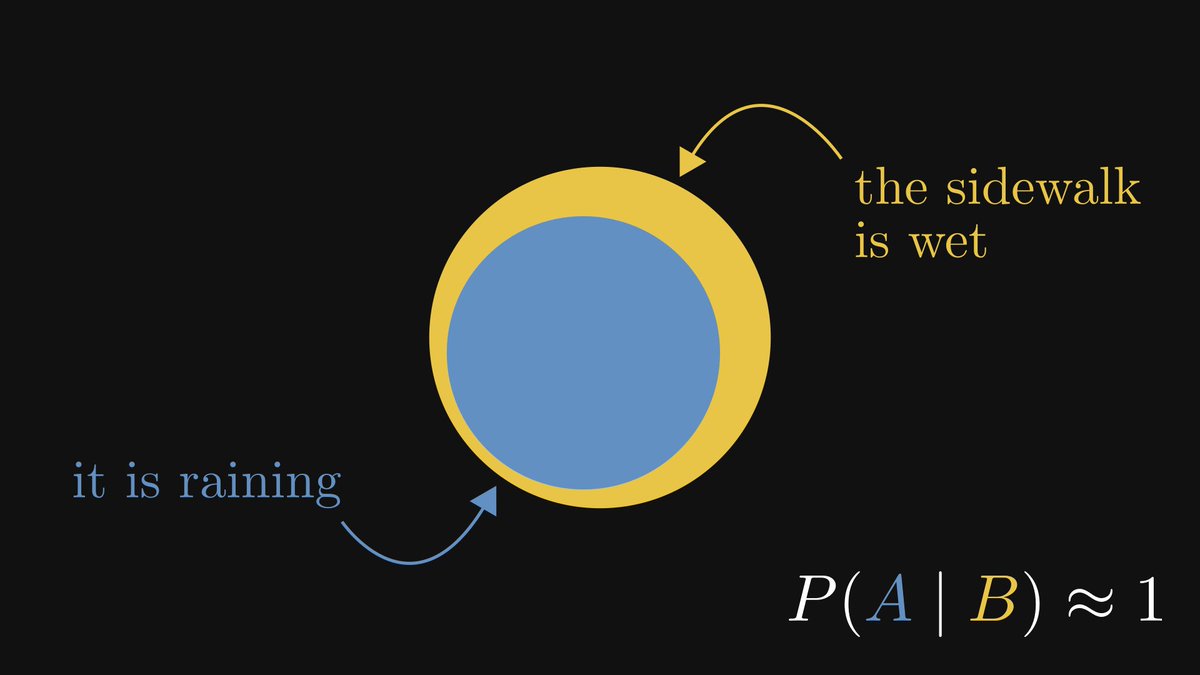
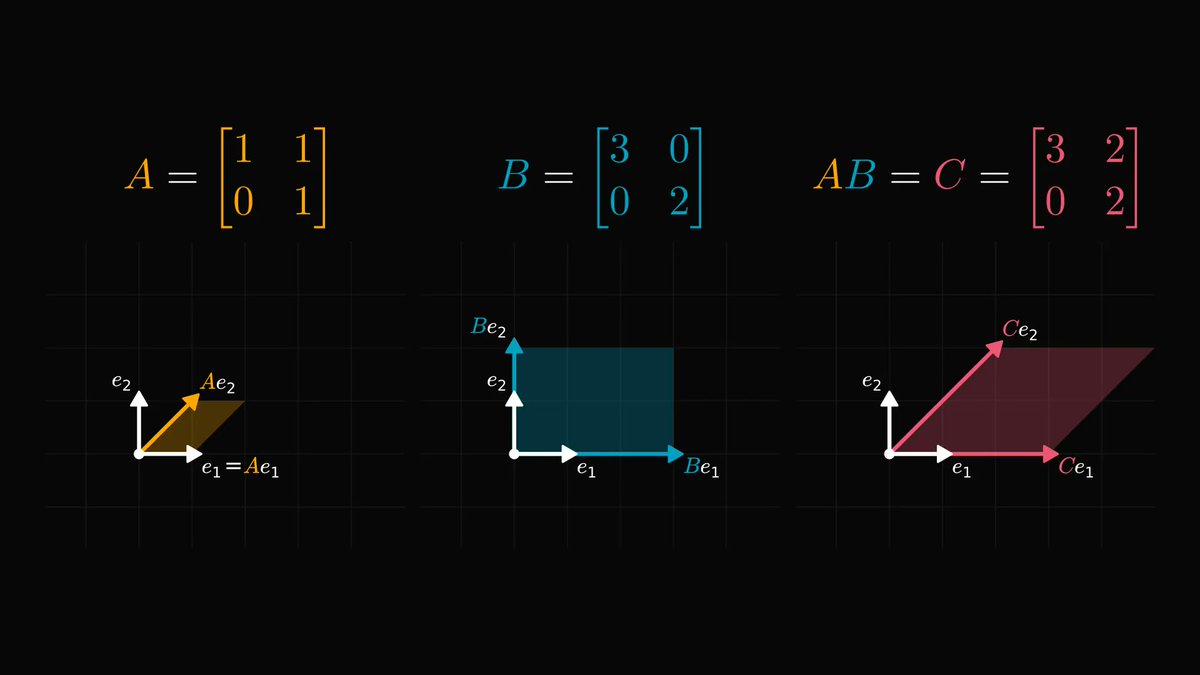If it is raining, the sidewalk is wet.
If the sidewalk is wet, is it raining? Not necessarily. Yet, we are inclined to think so. This is a common logical fallacy called "affirming the consequent".
However, it is not entirely wrong. Why? Enter the Bayes theorem:
If the sidewalk is wet, is it raining? Not necessarily. Yet, we are inclined to think so. This is a common logical fallacy called "affirming the consequent".
However, it is not entirely wrong. Why? Enter the Bayes theorem:

Propositions of the form "if A, then B" are called implications.
They are written as "A → B", and they form the bulk of our scientific knowledge.
Say, "if X is a closed system, then the entropy of X cannot decrease" is the 2nd law of thermodynamics.
They are written as "A → B", and they form the bulk of our scientific knowledge.
Say, "if X is a closed system, then the entropy of X cannot decrease" is the 2nd law of thermodynamics.
In the implication A → B, the proposition A is called "premise", while B is called the "conclusion".
The premise implies the conclusion, but not the other way around.
If you observe a wet sidewalk, it is not necessarily raining. Someone might have spilled a barrel of water.
The premise implies the conclusion, but not the other way around.
If you observe a wet sidewalk, it is not necessarily raining. Someone might have spilled a barrel of water.
Let's talk about probability!
Probability is an extension of classical logic, where the analogue of implication is the conditional probability.
Probability is an extension of classical logic, where the analogue of implication is the conditional probability.
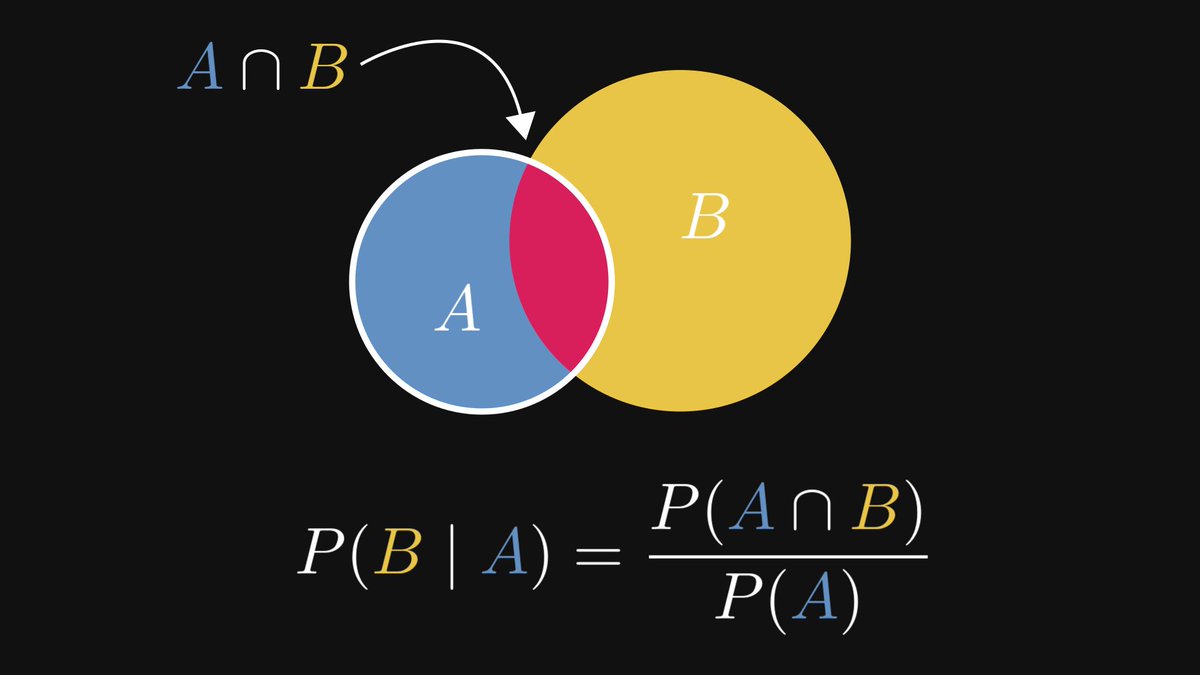
The closer P(B | A) to 1, the more likely B (the conclusion) becomes when observing A (the premise). 
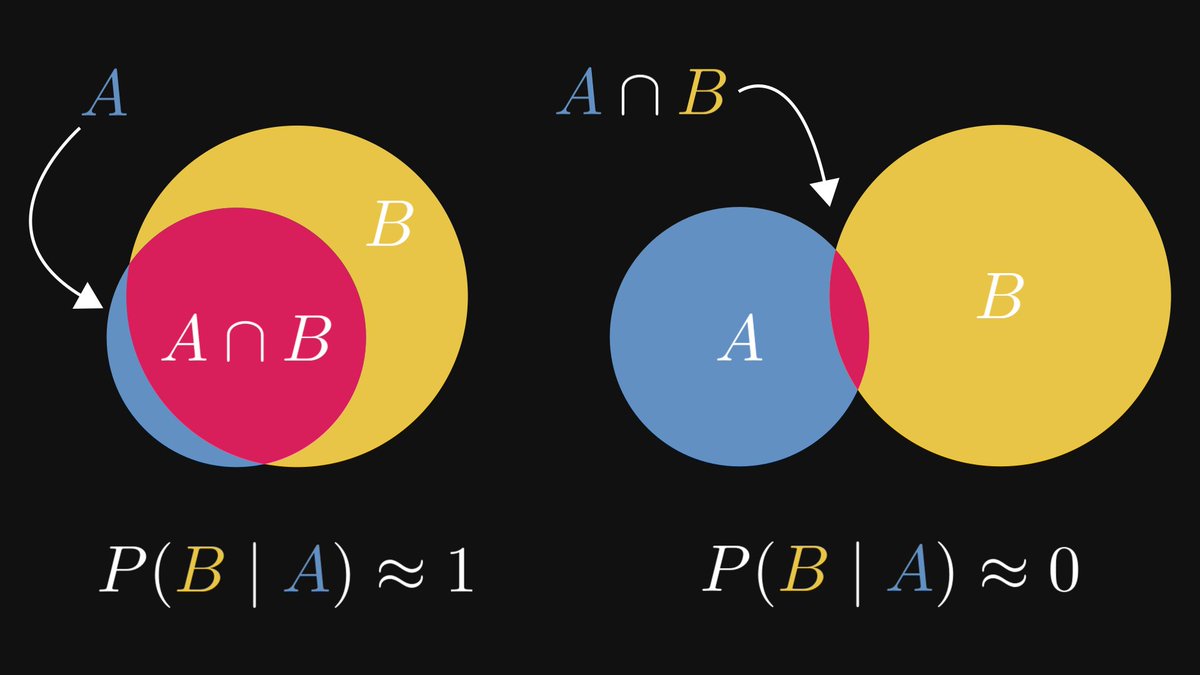
The Bayes theorem expresses P(A | B), the likelihood of the premise given that the conclusion is observed.
What's best: it relates P(A | B) to P(B | A). That is, it tells us if we can "affirm the consequent" or not!
What's best: it relates P(A | B) to P(B | A). That is, it tells us if we can "affirm the consequent" or not!
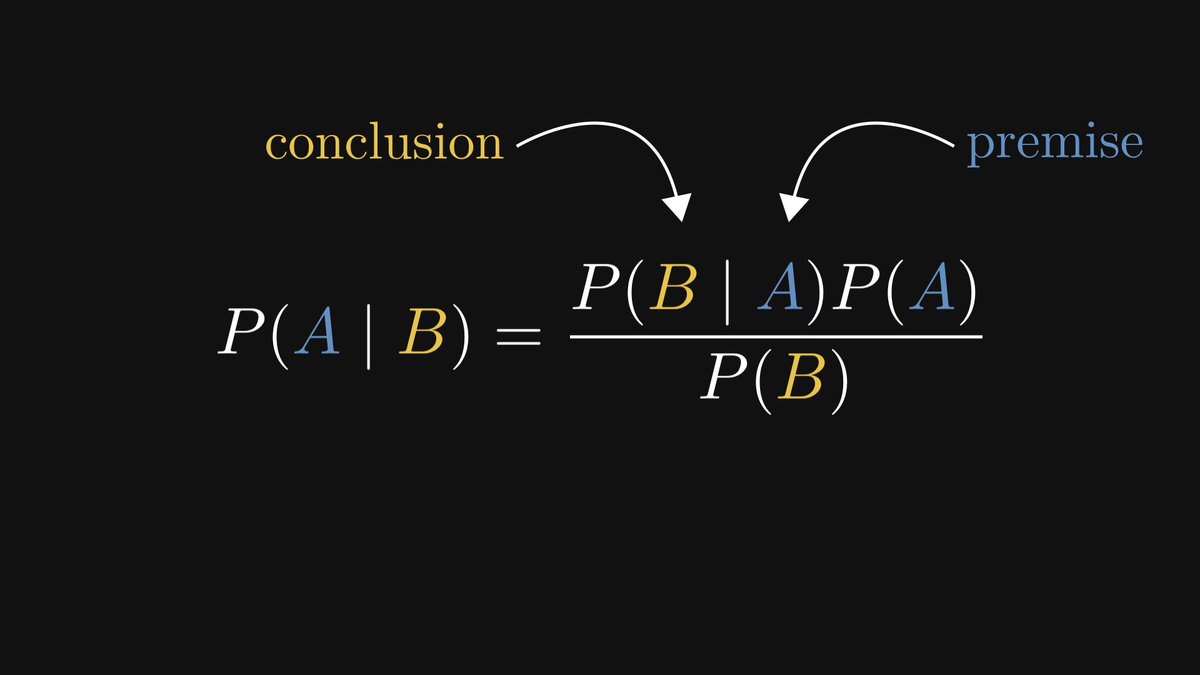
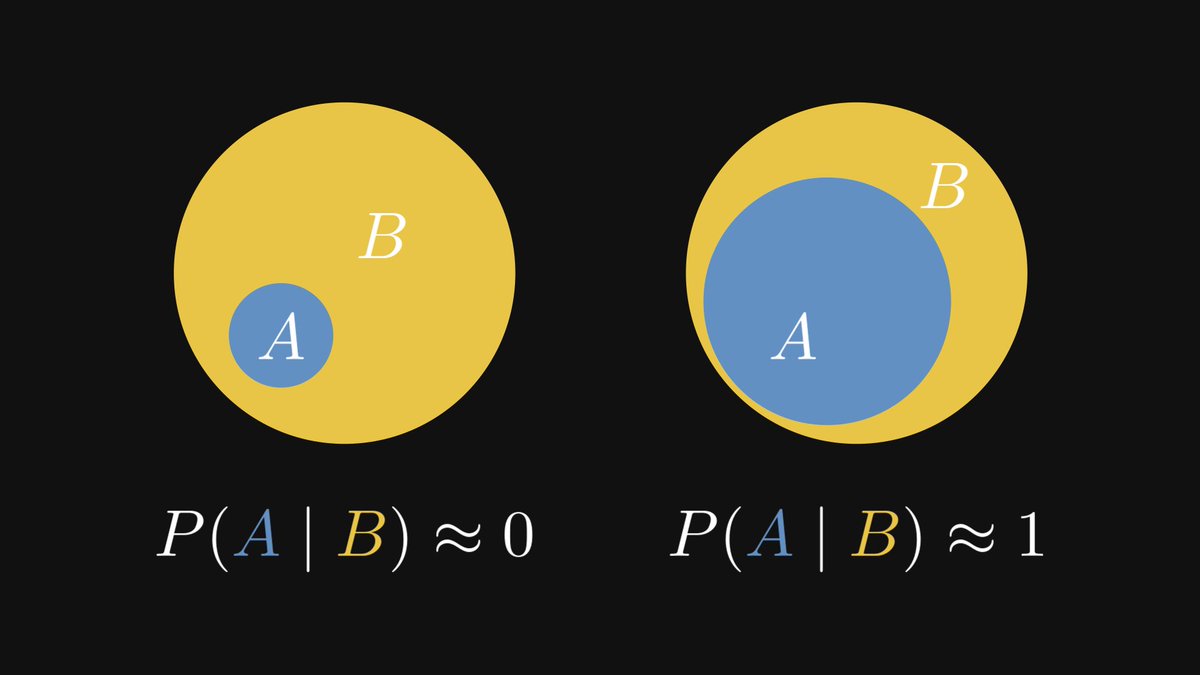
Suppose that the conclusion B undoubtedly follows from the premise A. (That is, P(B |A) = 1.)
How likely is the other way around? The Bayes theorem gives us an answer.
How likely is the other way around? The Bayes theorem gives us an answer.
Thus, when we take a glimpse at the sidewalk outside and see that it is soaking wet, it is safe to assume that it's raining.
The other explanations are fairly rare.
The other explanations are fairly rare.
Most machine learning practitioners don’t understand the math behind their models.
That's why I've created a FREE roadmap so you can master the 3 main topics you'll ever need: algebra, calculus, and probabilities.
Get the roadmap here: thepalindrome.org/p/the-roadmap-…
That's why I've created a FREE roadmap so you can master the 3 main topics you'll ever need: algebra, calculus, and probabilities.
Get the roadmap here: thepalindrome.org/p/the-roadmap-…
• • •
Missing some Tweet in this thread? You can try to
force a refresh