Thread by @TivadarDanka

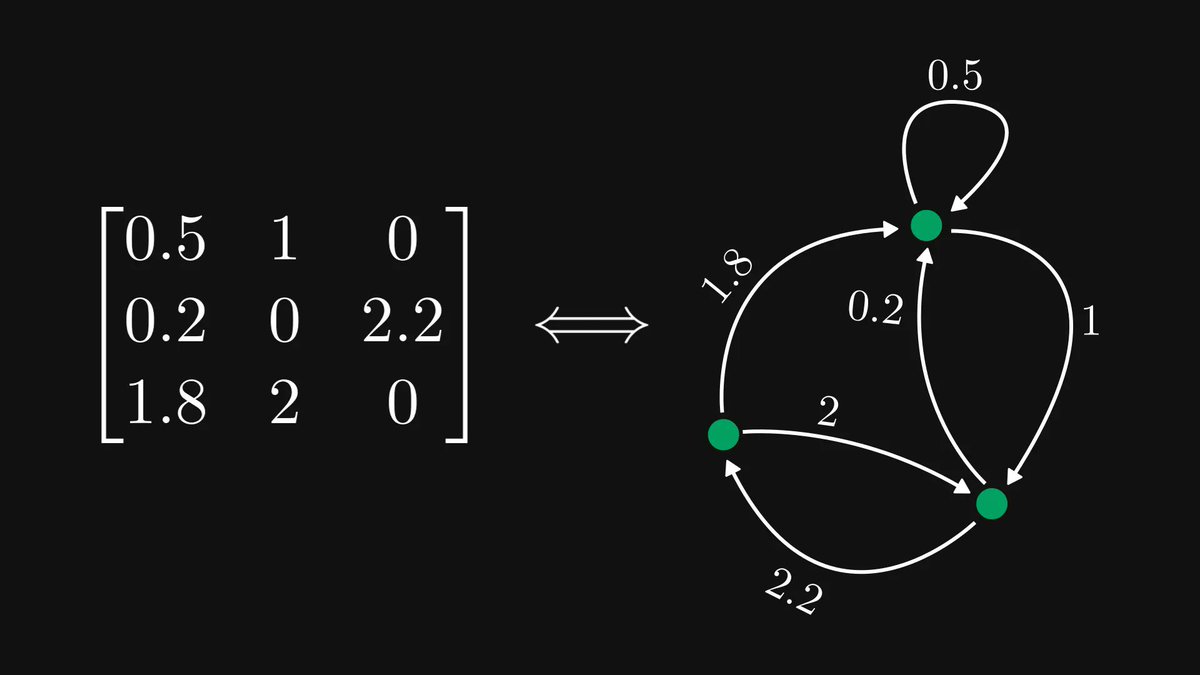
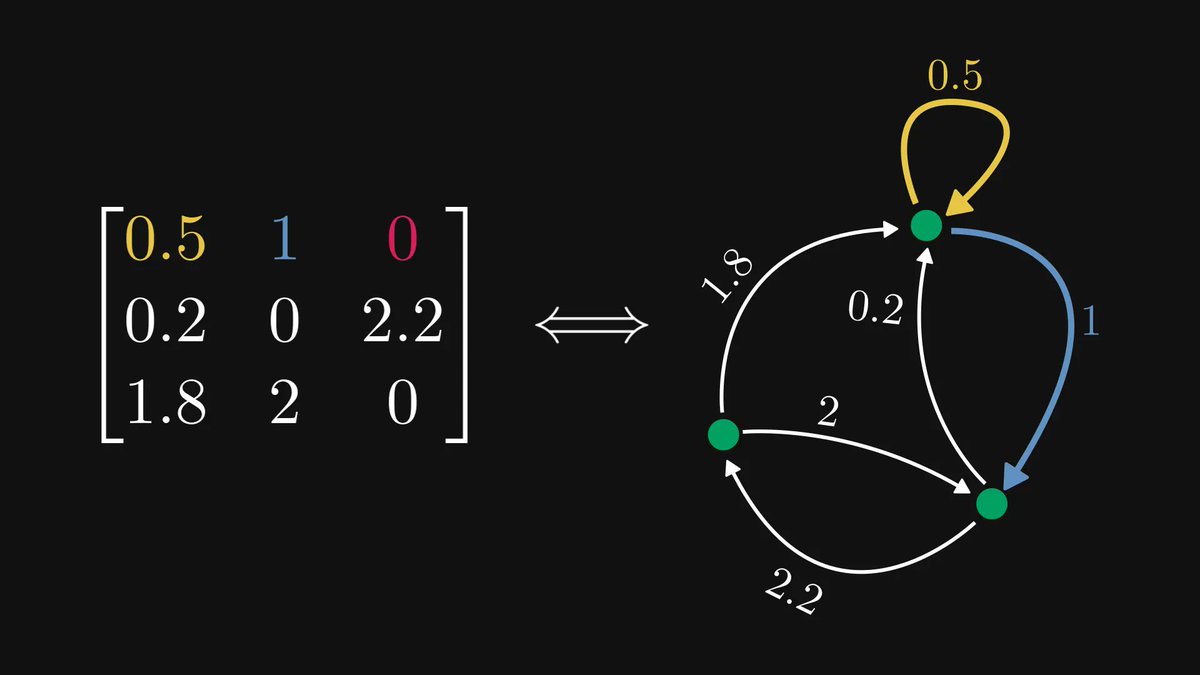
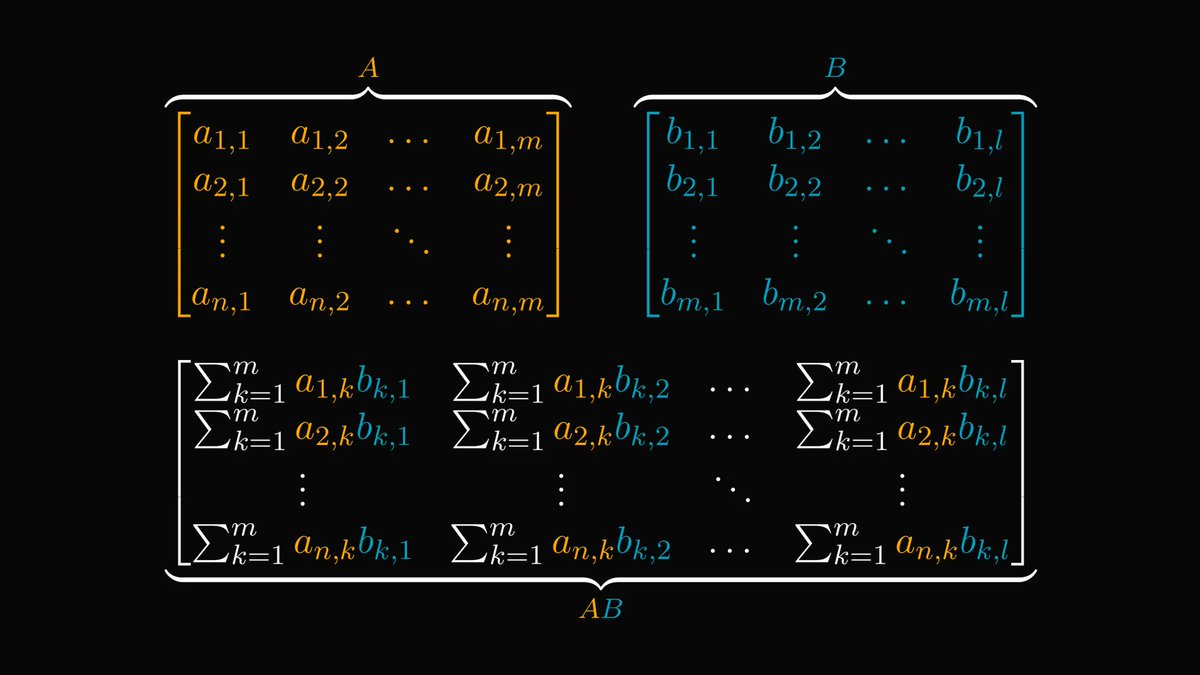
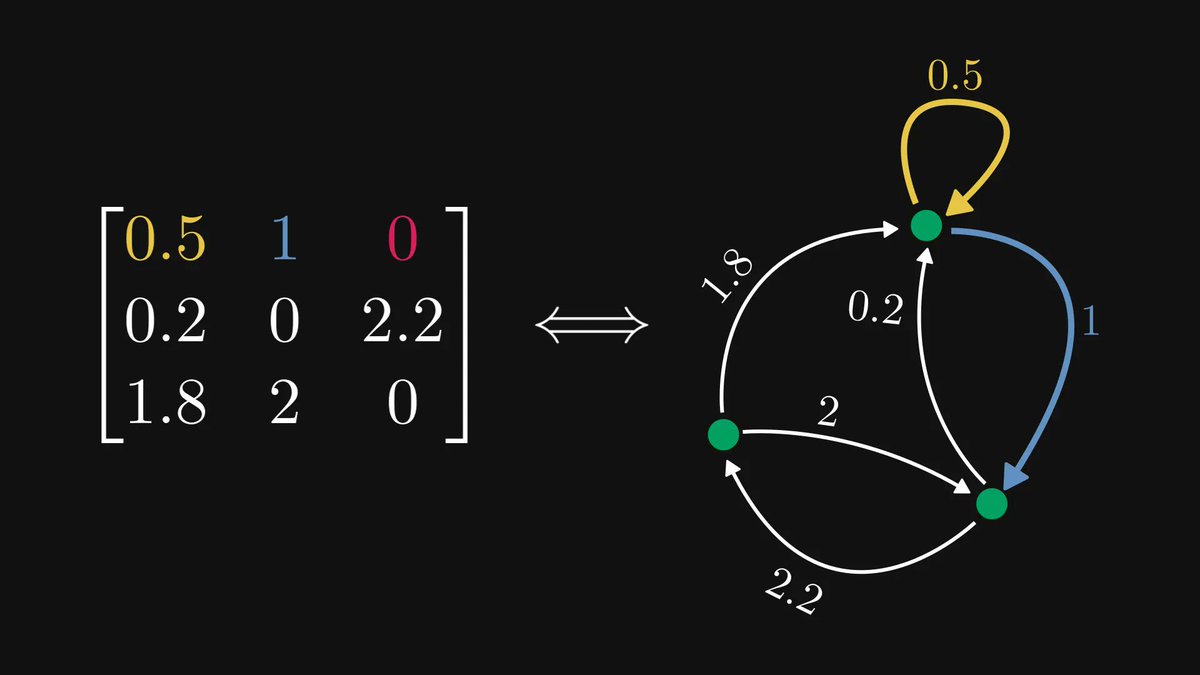
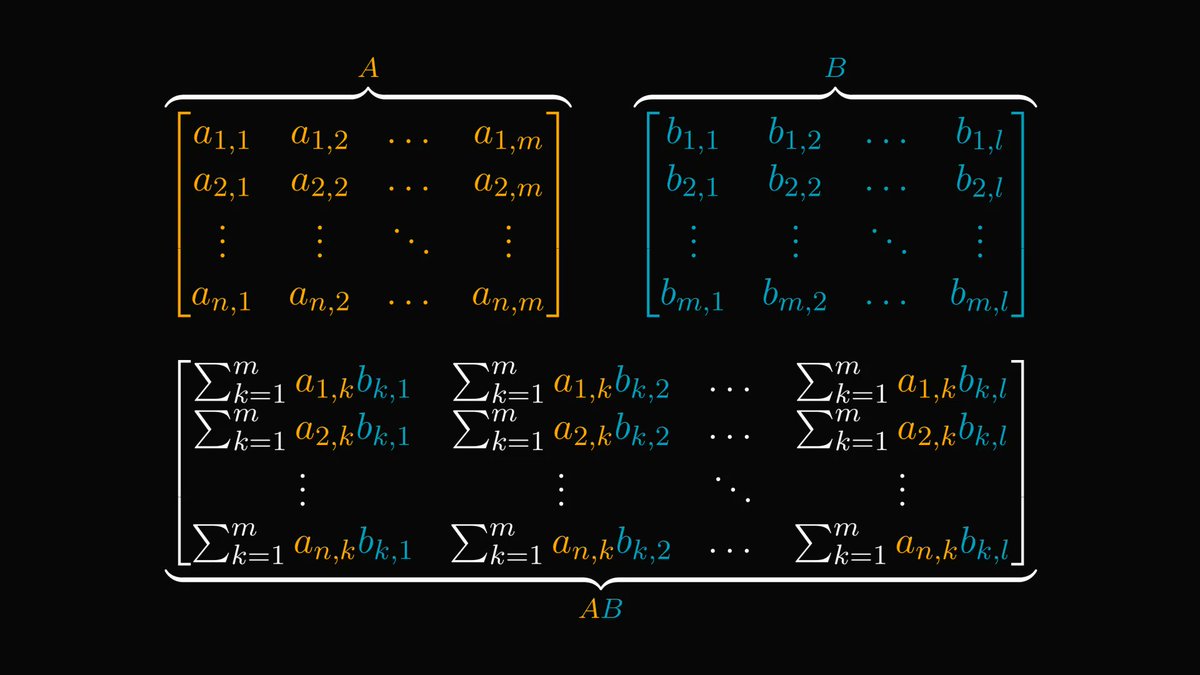
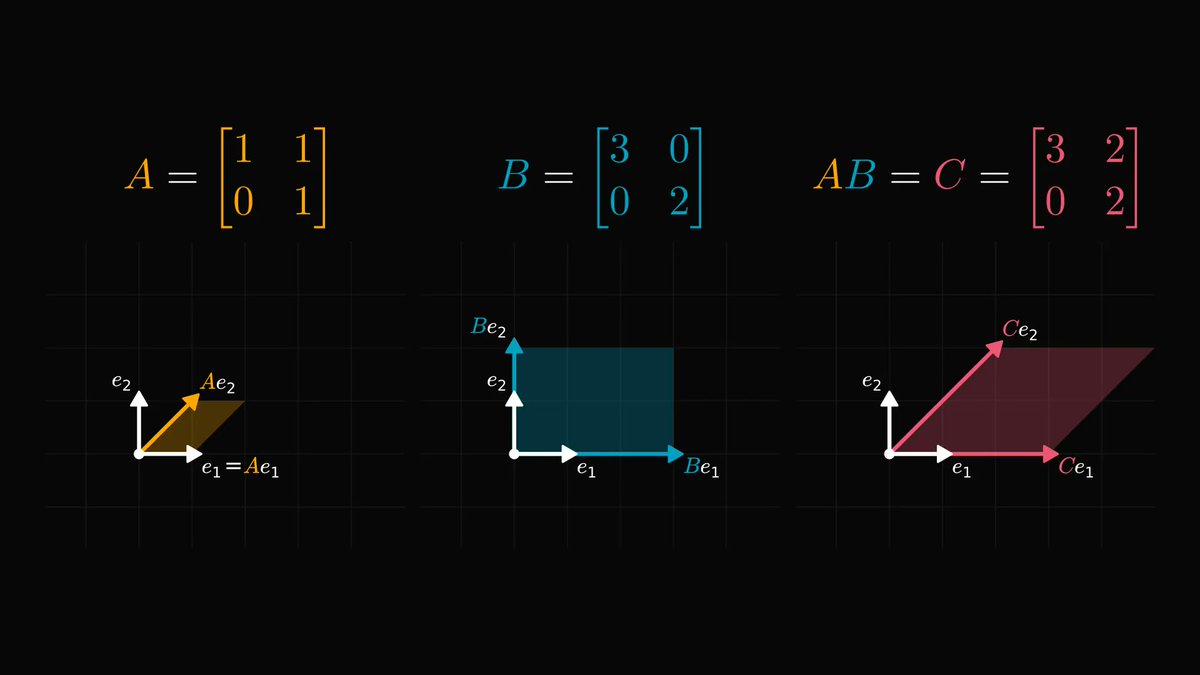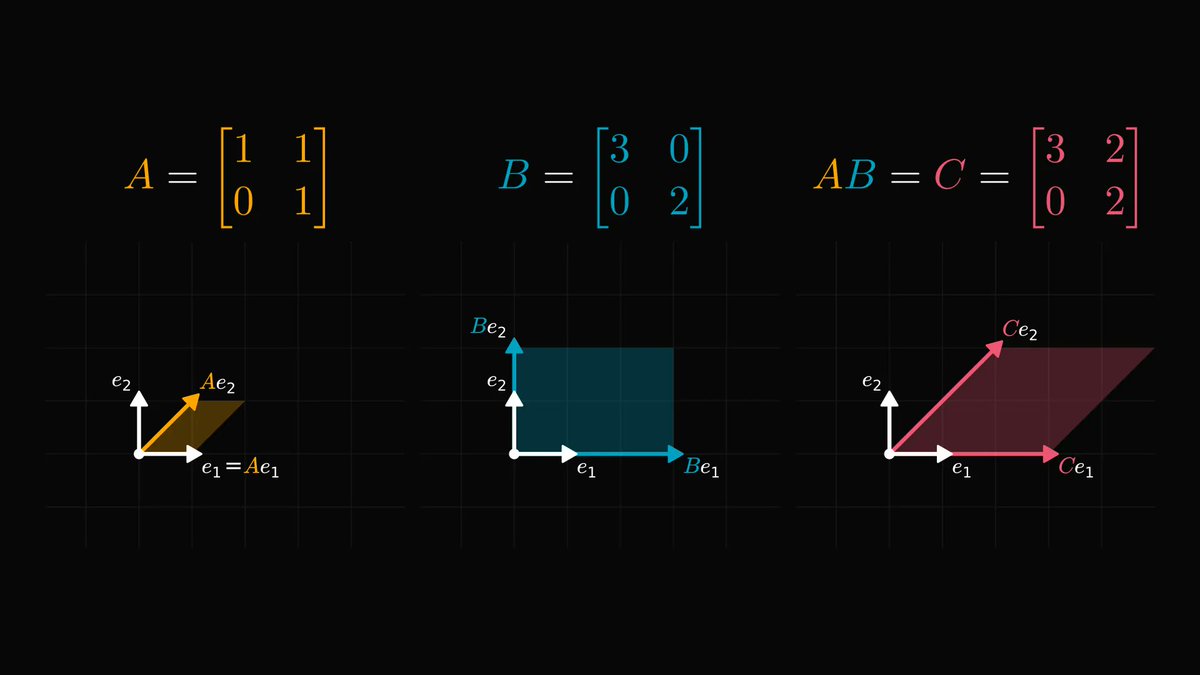The following multiplication method makes everybody wish they had been taught math like this in school.

It's not just a cute visual tool: it illuminates how and why long multiplication works.

Here is the full story:

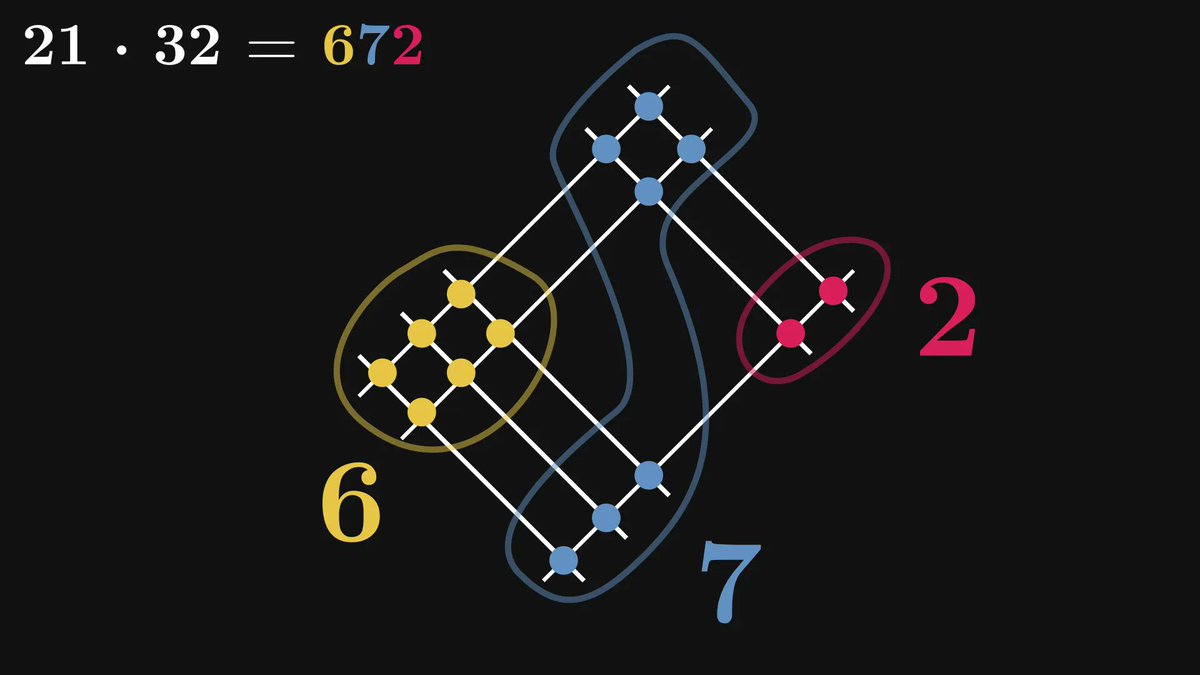
First, the method.

The first operand (21 in our case) is represented by two groups of lines: two lines in the first (1st digit), and one in the second (2nd digit).

One group for each digit.

Similarly, the second operand (32) is encoded with two groups of lines, one for each digit.

These lines are perpendicular to the previous ones.

Now comes the magic.

Count the intersections among the lines. Turns out that they correspond to the digits of the product 21 · 32.

What is this sorcery?

Let’s decompose the operands into tens and ones before multiplying them together.

By carrying out the product term by term, we are doing the same thing!

Here it is, visualized on our line representation.

There’s more. How do we multiply 21 · 32 by hand?

First, we calculate 21 · 30 = 630, then 21 · 2 = 42, which we sum up to get 21 · 32 = 672.

We learn this at elementary school like a cookbook recipe: we don’t learn the why, just the how.

Why is this relevant?

Because this is exactly what happens with the Japanese multiplication method!

Check this out one more time.

What’s the lesson here?

That visual and algebraic thinking go hand in hand. The Japanese method neatly illustrates how multiplication works, but with the algebra behind it, we feel the pulse of long multiplication.

We are not just mere users; we see behind the curtain now.

Most machine learning practitioners don’t understand the math behind their models.

That's why I've created a FREE roadmap so you can master the 3 main topics you'll ever need: algebra, calculus, and probabilities.

Get the roadmap here: thepalindrome.org/p/the-roadmap-…