Claim: gpt-5-pro can prove new interesting mathematics.
Proof: I took a convex optimization paper with a clean open problem in it and asked gpt-5-pro to work on it. It proved a better bound than what is in the paper, and I checked the proof it's correct.
Details below.
Proof: I took a convex optimization paper with a clean open problem in it and asked gpt-5-pro to work on it. It proved a better bound than what is in the paper, and I checked the proof it's correct.
Details below.
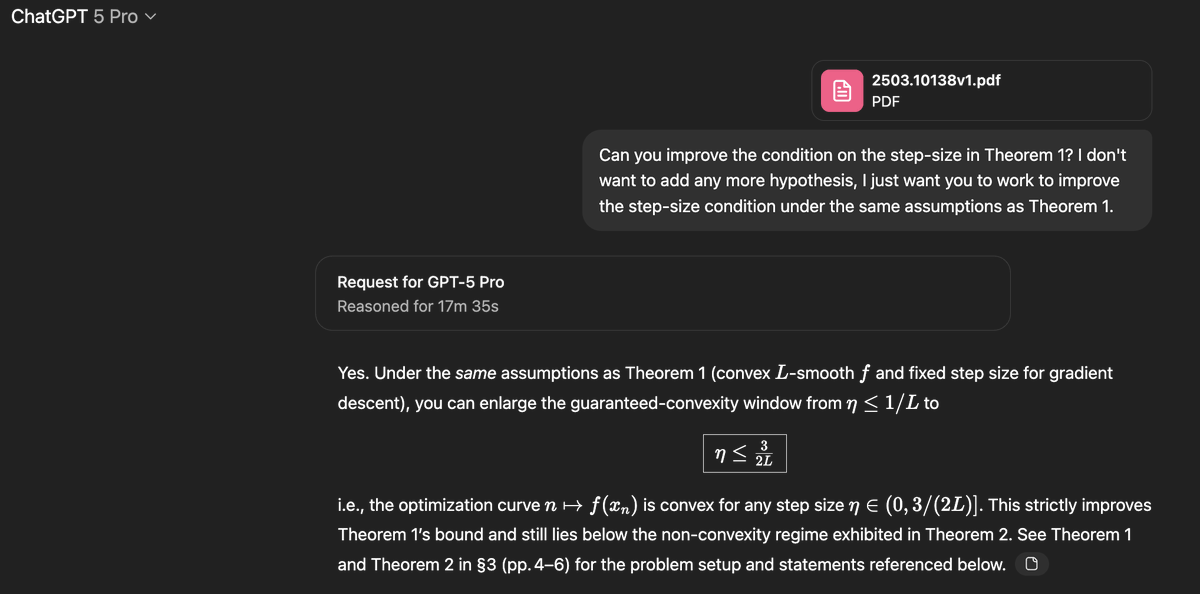
The paper in question is this one which studies the following very natural question: in smooth convex optimization, under what conditions on the stepsize eta in gradient descent will the curve traced by the function value of the iterates be convex?arxiv.org/pdf/2503.10138…
In the v1 of the paper they prove that if eta is smaller than 1/L (L is the smoothness) then one gets this property, and if eta is larger than 1.75/L then they construct a counterexample. So the open problem was: what happens in the range [1/L, 1.75/L].
As you can see in the top post, gpt-5-pro was able to improve the bound from this paper and showed that in fact eta can be taken to be as large as 1.5/L, so not quite fully closing the gap but making good progress. Def. a novel contribution that'd be worthy of a nice arxiv note.
Now the only reason why I won't post this as an arxiv note, is that the humans actually beat gpt-5 to the punch :-). Namely the arxiv paper has a v2 with an additional author and they closed the gap completely, showing that 1.75/L is the tight bound.arxiv.org/pdf/2503.10138…
And yeah the fact that it proves 1.5/L and not the 1.75/L also shows it didn't just search for the v2. Also the above proof is very different from the v2 proof, it's more of an evolution of the v1 proof.
• • •
Missing some Tweet in this thread? You can try to
force a refresh