Thread by @predict_addict

The most honest math you'll ever use. 🤝

The Maximum Entropy Principle (MaxEnt) is a genius rule for modeling with incomplete data. It tells you to:

✅ Respect what you KNOW.
🚫 Assume nothing else.

It's the reason behind: Logistic Regression, Gaussian distributions, and smarter AI exploration.

Here’s how it works and why it matters: 👇

Think about the last time you built a model. You had some data—a few key averages, a couple of constraints. But beyond that?

❓ A vast ocean of uncertainty.

❌ The temptation is to fill in the gaps with assumptions. But what if those assumptions are wrong? You’ve just baked your own bias into the model.

✅ There's a smarter, more humble way: The Maximum Entropy Principle (MaxEnt).

It’s the mathematical embodiment of the wisdom: "Only say what you know."

♟️ The Game of Limited Information

Imagine you're a detective with only three clues. Or a gambler who only knows the average roll of a die. How do you guess the entire probability distribution?

Do you invent complex rules? Or do you choose the simplest, most unbiased guess possible?

MaxEnt argues for the latter. It's a formal rule for navigating ignorance:

Given what you do know, choose the probability distribution that is maximally uncertain.

You respect the evidence completely but assume nothing else. No hidden agendas. No fluff.

⚖️ The Scale of Uncertainty: What Is Entropy?

In information theory, entropy isn't about disorder. It's about surprise.

H
[
p
]
=
−
∑
x
p
(
x
)
log
⁡
p
(
x
)
H[p]=−
x
∑
​
p(x)logp(x)

A high-entropy distribution is deeply unpredictable. A low-entropy one is full of hidden patterns and structure. MaxEnt chooses the distribution that is as surprised as you are, given the data.

🧠 MaxEnt in 3 Acts: From Ignorance to Insight

The power of this principle is how it generates famous results from minimal information:

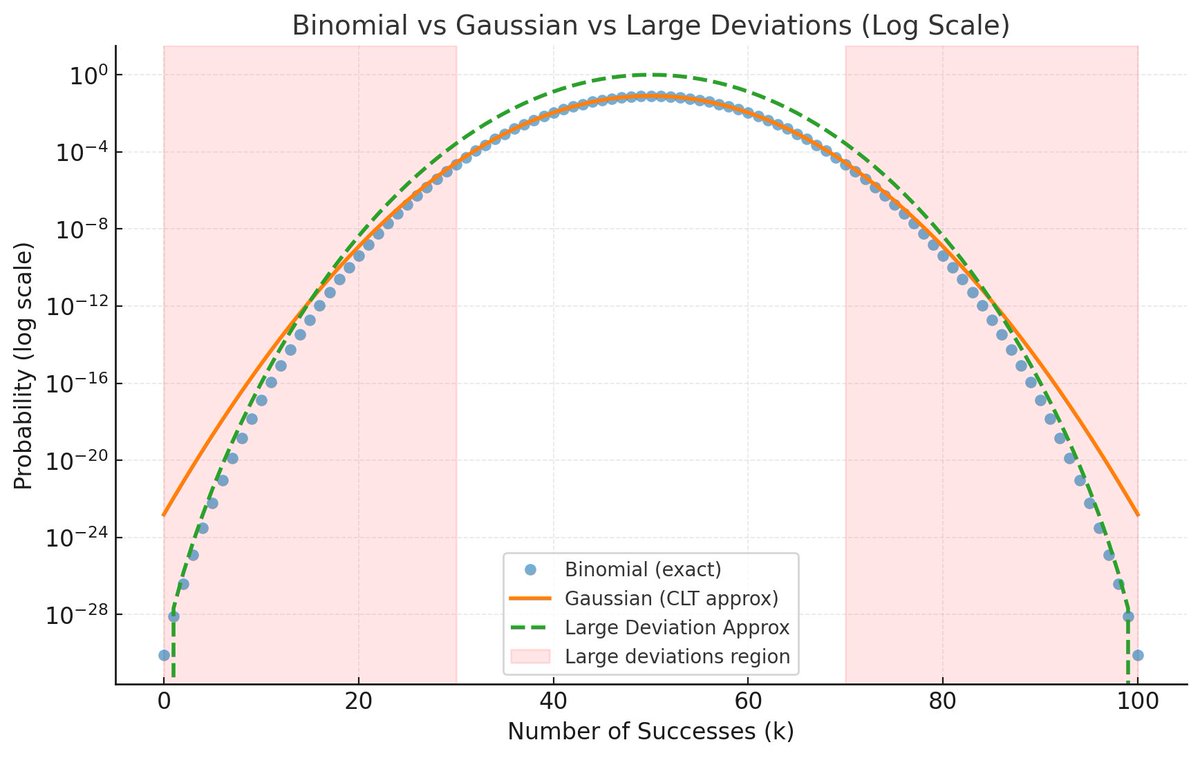
Act I: You know nothing. → All you know is that probabilities must sum to 1. MaxEnt gives you the Uniform Distribution. The ultimate shrug of the shoulders. Perfect ignorance.

Act II: You know the average. → You know the mean energy of particles in a system. MaxEnt derives the Boltzmann Distribution—the very foundation of statistical mechanics. A cornerstone of physics, from one simple constraint.
Act III: You know the spread. → You know the mean and the variance.

MaxEnt hands you the Gaussian (Normal) Distribution. The bell curve isn't just common; it's the least biased shape for that information.
🔗 The Unbreakable Link to Occam's Razor

You've heard the ancient advice: "The simplest explanation is usually the best."

MaxEnt is Occam's Razor for probability distributions.

It doesn't prefer simplicity for simplicity's sake. It prefers the least assumptive model. It aggressively shaves away any structure not demanded by your data. This isn't a preference; it's a principle of honesty.

🤖 Why This is a Secret Weapon in Machine Learning

This isn't abstract philosophy. MaxEnt is the silent engine under the hood of countless ML algorithms:

Logistic Regression / Softmax: The go-to classifier? It's literally a MaxEnt model.

For example, it finds the weights that match the feature means in your data and nothing more.
Reinforcement Learning: Modern RL (e.g., Soft Actor-Critic) uses MaxEnt policies to maximize not just reward, but exploration. It keeps agents from becoming overconfident too early.

Natural Language Processing: The entire "MaxEnt Markov Model" family was built on this principle for tasks like part-of-spepeech tagging.
The Exponential Family: That entire class of distributions (Gaussian, Exponential, Bernoulli, etc.)?

They all fall out naturally from applying MaxEnt under different constraints. They are the least biased choices for their known quantities.
🧭 The Ultimate Takeaway

The Maximum Entropy Principle is a discipline. A commitment to intellectual honesty in a world of uncertainty.

Capture what you know. Be maximally agnostic about what you don't.

It’s a framework that prevents us from lying to ourselves with our models. And in an age of complex AI, that might be the most powerful feature of all.

✨ Look around you. That softmax output? That Gaussian prior?

That Boltzmann exploration? You're not just looking at math. You're looking at a profound respect for the limits of knowledge.

What do you think? Is embracing uncertainty the key to better models?

#MachineLearning #AI #DataScience #Mathematics #InformationTheory #Physics #OccamsRazor #MaxEnt #ArtificialIntelligence