
Experienced Data Science Leader | PhD in Machine Learning | 4x Author | Black Belt 🥋 in Time Series | Chief Conformal Prediction Promoter| Mathematician |
4 subscribers
How to get URL link on X (Twitter) App


 The ecosystem has moved forward with specialized libraries (XGBoost, LightGBM, CatBoost), distributed frameworks (Dask), and AutoML tools. But there’s still no unified, modern toolkit that combines:
The ecosystem has moved forward with specialized libraries (XGBoost, LightGBM, CatBoost), distributed frameworks (Dask), and AutoML tools. But there’s still no unified, modern toolkit that combines:
 How can you make any predictions then? Enter Chebyshev’s Inequality —probability's most reliable safety net.
How can you make any predictions then? Enter Chebyshev’s Inequality —probability's most reliable safety net.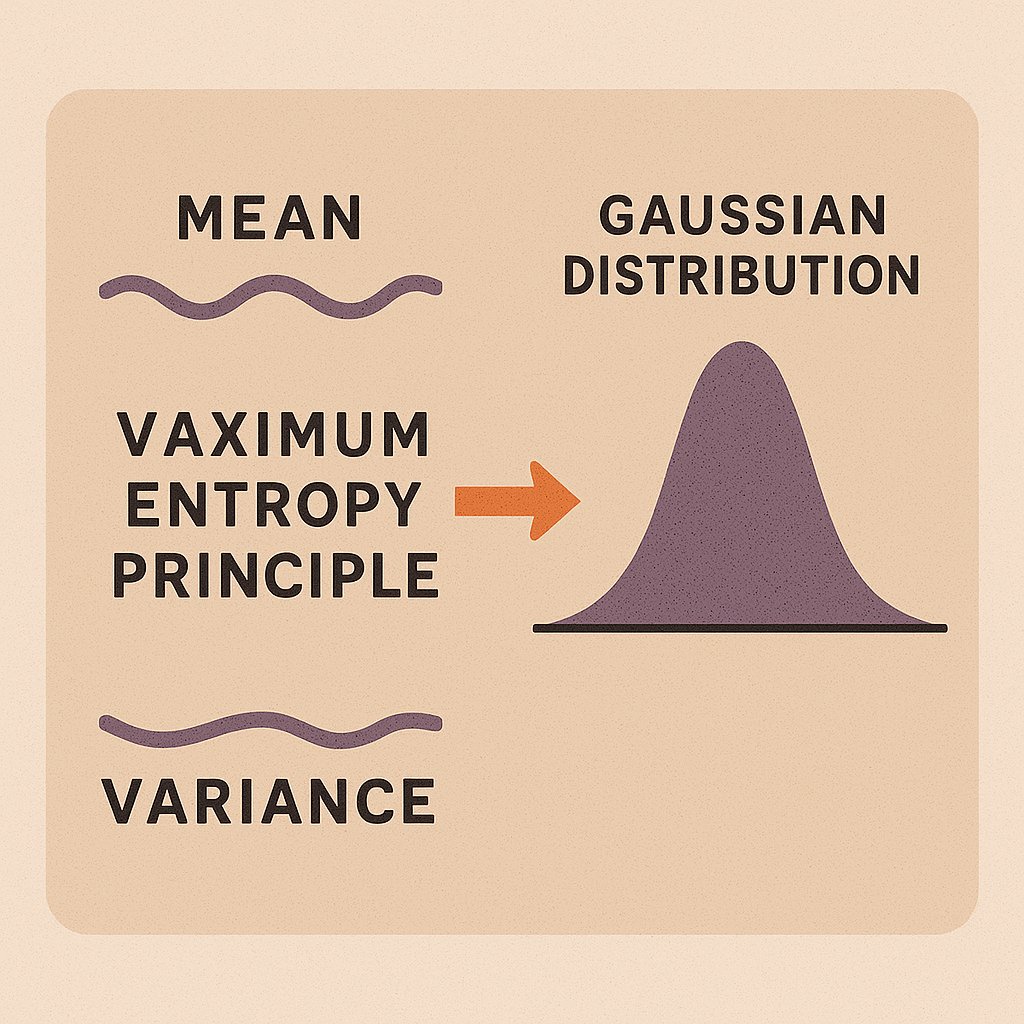
 Among them, the Gaussian distribution (a.k.a. the bell curve) is perhaps the most iconic. But why does it appear so often? And why does MaxEnt single it out?
Among them, the Gaussian distribution (a.k.a. the bell curve) is perhaps the most iconic. But why does it appear so often? And why does MaxEnt single it out?
 He was racing against the sunrise, feverishly scribbling equations that would change the world.
He was racing against the sunrise, feverishly scribbling equations that would change the world.
 It's the reason behind: Logistic Regression, Gaussian distributions, and smarter AI exploration.
It's the reason behind: Logistic Regression, Gaussian distributions, and smarter AI exploration.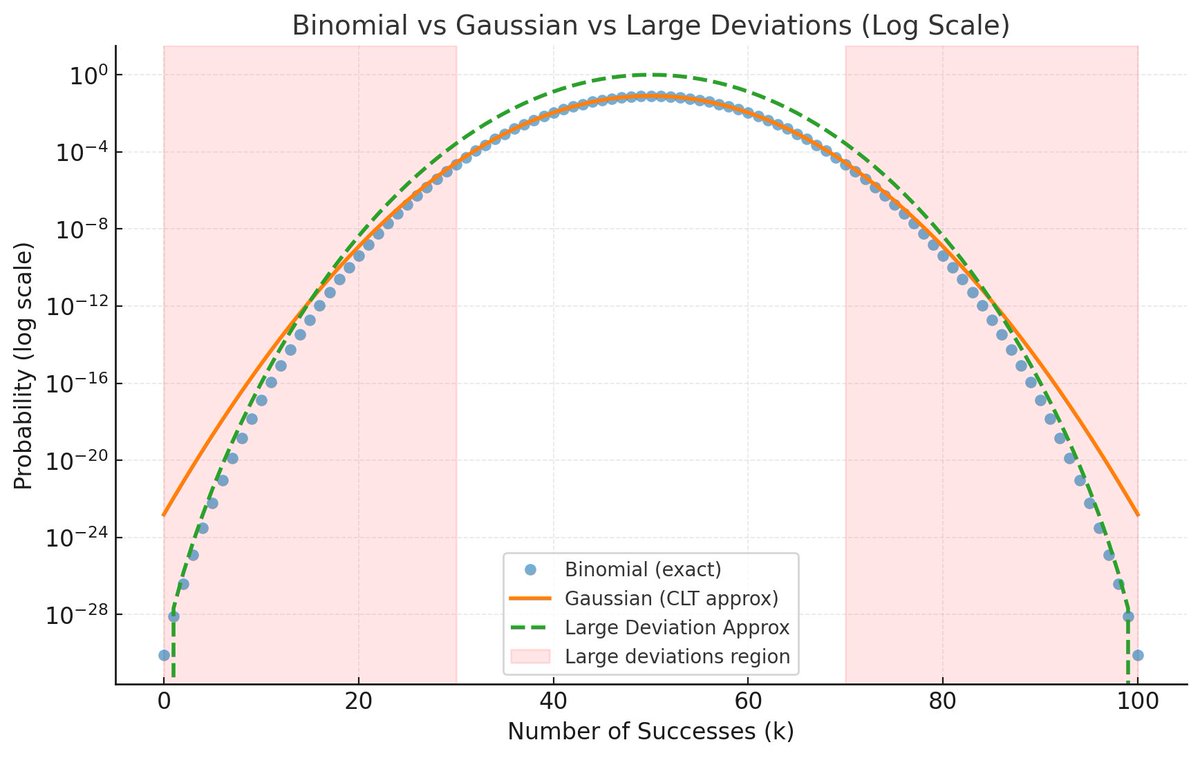
 The CLT describes what happens near the average, within fluctuations of order √n. That’s the “bulk” of the distribution.
The CLT describes what happens near the average, within fluctuations of order √n. That’s the “bulk” of the distribution.
 His work was brilliant, concise, and transformative.
His work was brilliant, concise, and transformative.
 * H(Y): Total uncertainty in Y (right circle)
* H(Y): Total uncertainty in Y (right circle)
 On the other, Andrey Markov - sharp, stubborn, and about to make history—declares: "Not so fast."
On the other, Andrey Markov - sharp, stubborn, and about to make history—declares: "Not so fast."
 Fourier provided little justification for when such series converge or what kinds of functions they truly represent.
Fourier provided little justification for when such series converge or what kinds of functions they truly represent. 
 It's important to note that the modern foundations of machine learning were largely shaped in places like the USSR and the USA—not the UK.
It's important to note that the modern foundations of machine learning were largely shaped in places like the USSR and the USA—not the UK. 
 Those who excel at forecasting often come from a strong econometrics background, understanding deeply rooted concepts like autoregression, stationarity, and lagged dependencies—ideas established nearly a century ago by statisticians like Yule.
Those who excel at forecasting often come from a strong econometrics background, understanding deeply rooted concepts like autoregression, stationarity, and lagged dependencies—ideas established nearly a century ago by statisticians like Yule.

 🔍 What Is Spectral Entropy? Think "Radio Stations"!
🔍 What Is Spectral Entropy? Think "Radio Stations"!
 At a time when probability was largely limited to independent events like coin flips or dice rolls, Markov broke new ground. He showed how we could still apply the laws of probability – such as the law of large numbers – to systems where each event depends on the previous one.
At a time when probability was largely limited to independent events like coin flips or dice rolls, Markov broke new ground. He showed how we could still apply the laws of probability – such as the law of large numbers – to systems where each event depends on the previous one.

 Before Fourier, giants like Euler and Bernoulli dared to ask: “Can complex vibrations be built from simple waves?” But it was all speculation—no proof, just raw genius chasing an idea too wild to tame.
Before Fourier, giants like Euler and Bernoulli dared to ask: “Can complex vibrations be built from simple waves?” But it was all speculation—no proof, just raw genius chasing an idea too wild to tame.
 Some made lurid claims about how KANs wouldn’t scale, wouldn’t generalize, and certainly wouldn’t touch Transformers.
Some made lurid claims about how KANs wouldn’t scale, wouldn’t generalize, and certainly wouldn’t touch Transformers.
 🇺🇸 Wiener, with his applied wartime work, and 🇷🇺 Kolmogorov, with his deep theoretical insights, independently showed that if you know a process’s mean and covariance structure, you can build the optimal linear forecast—and even compute its error.
🇺🇸 Wiener, with his applied wartime work, and 🇷🇺 Kolmogorov, with his deep theoretical insights, independently showed that if you know a process’s mean and covariance structure, you can build the optimal linear forecast—and even compute its error.

 A groundbreaking method of signal filtering—now called the Wiener Filter.
A groundbreaking method of signal filtering—now called the Wiener Filter.
 🔁 Slutsky showed that when you apply moving averages (or rolling summations) to random data, the result can look surprisingly cyclical—even though there's no real underlying pattern. Just white noise + smoothing = the illusion of a cycle.
🔁 Slutsky showed that when you apply moving averages (or rolling summations) to random data, the result can look surprisingly cyclical—even though there's no real underlying pattern. Just white noise + smoothing = the illusion of a cycle.
 Here's why practitioners and researchers should be cautious:
Here's why practitioners and researchers should be cautious: