Thread by @wesg52

New paper! We reverse engineered the mechanisms underlying Claude Haiku’s ability to perform a simple “perceptual” task. We discover beautiful feature families and manifolds, clean geometric transformations, and distributed attention algorithms!

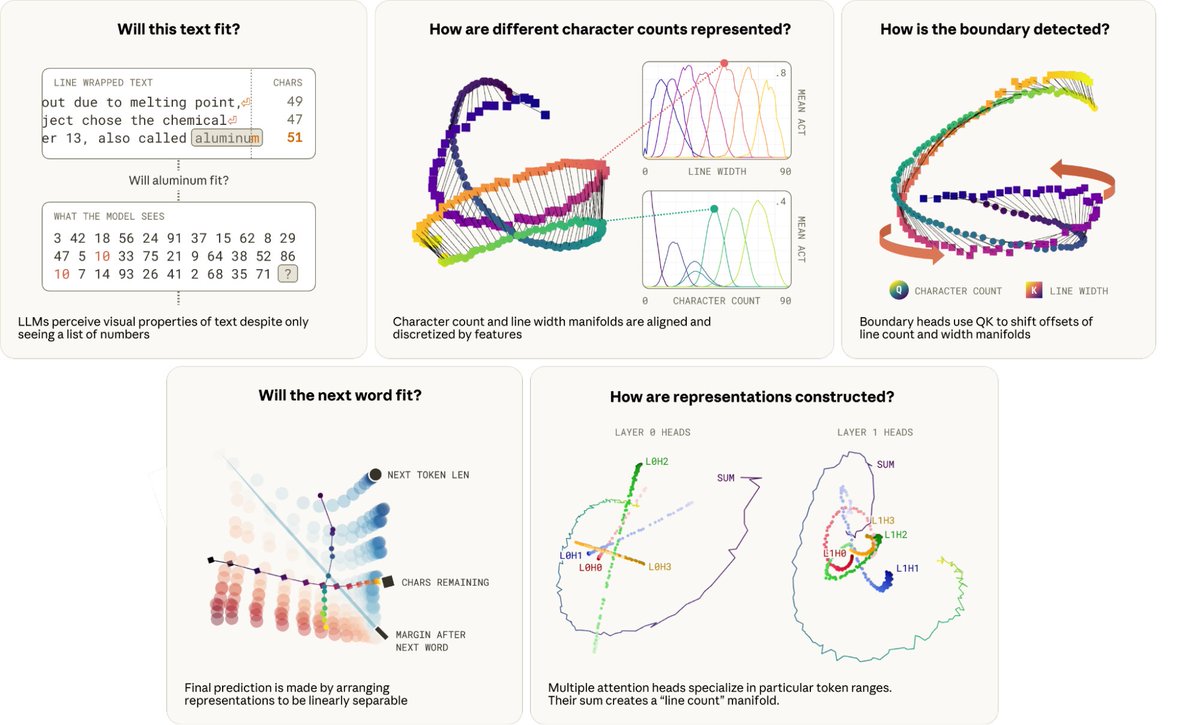
The task is simply when to break a line in fixed width text. This requires the model to in-context learn the line width constraint, state track the characters in the current line, compute the characters remaining, and determine if the next word fits!

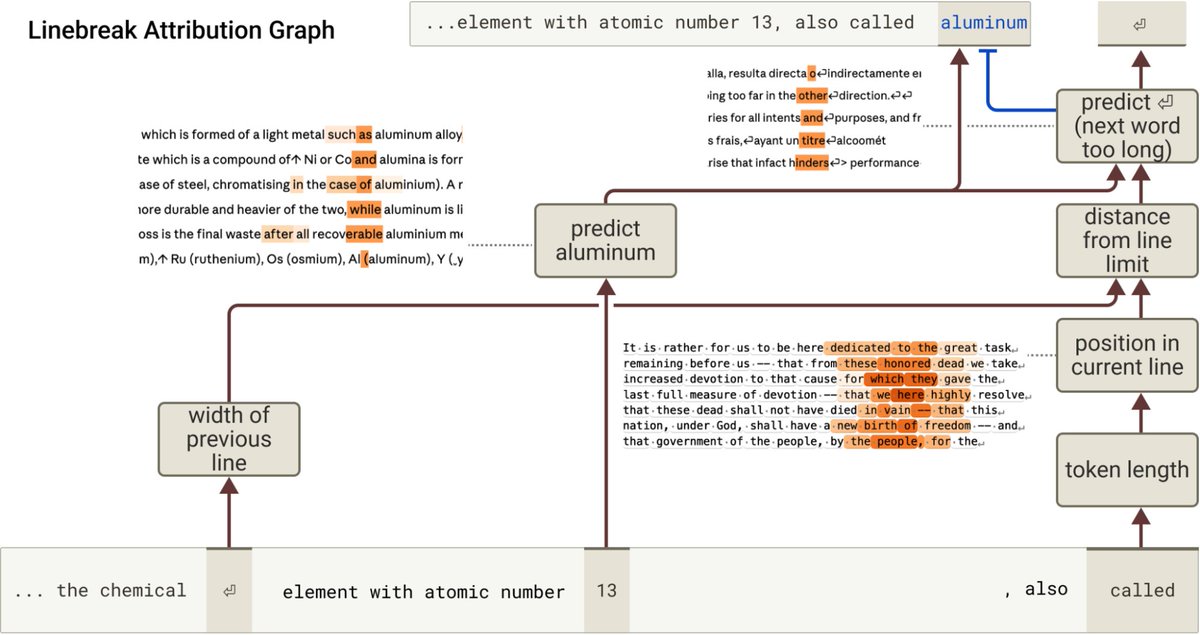
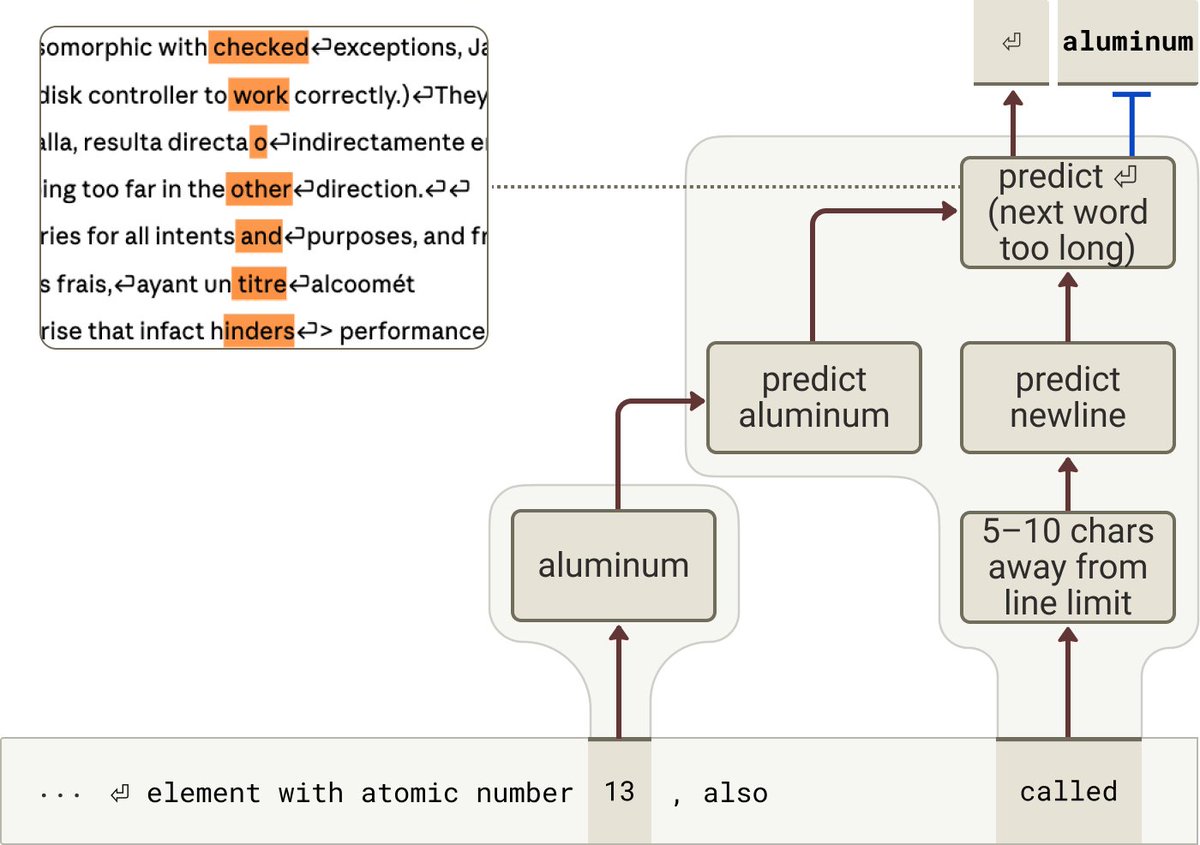
To get oriented, we made an attribution graph which surfaces features for each of the important parts of the computation: different counting features for each type of count, the natural next word, and a feature for detecting the next word exceeds the characters remaining.

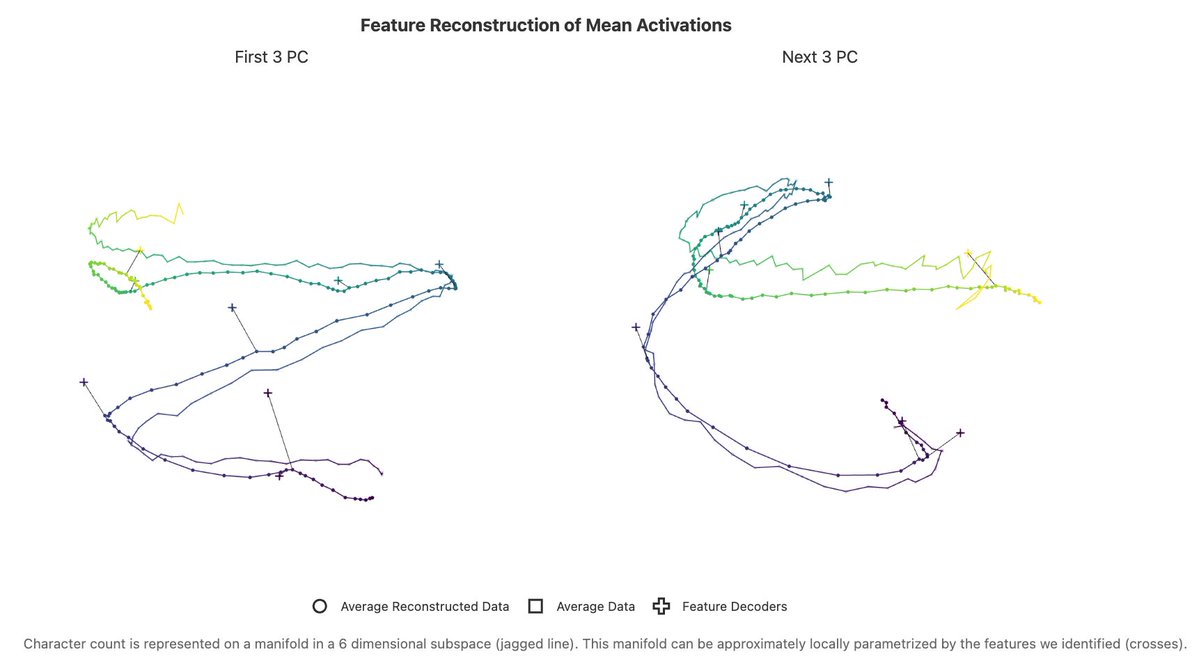
When looking at a broader dataset, we see larger feature families, like character counting features for the current character position in a line! These features are universal across dictionaries and resemble place cells in brains and curve detectors in vision networks.

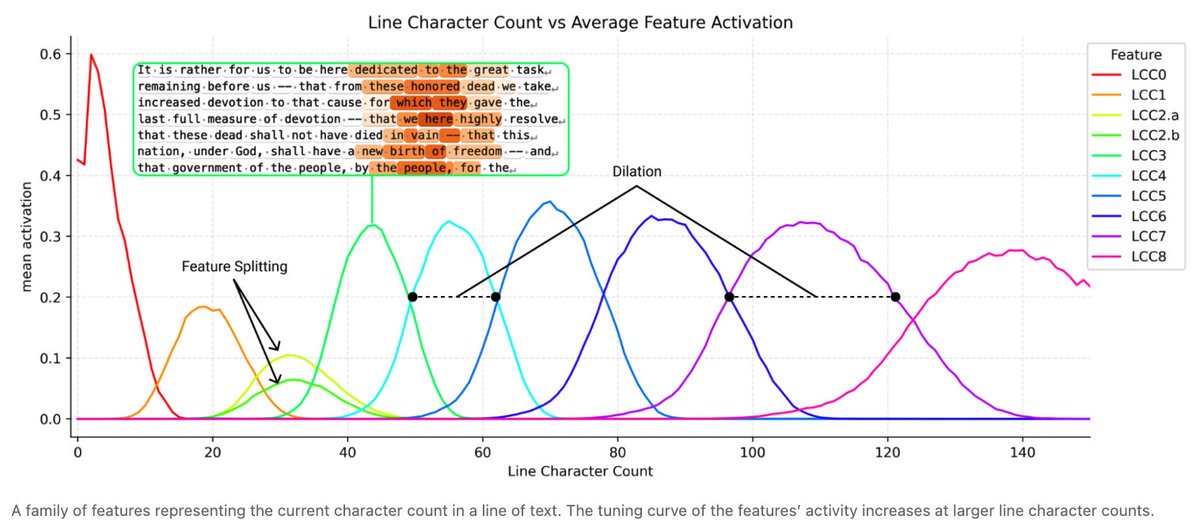
These counting features discretize a continuous counting manifold. The “rippled” representations are optimal with respect to balancing capacity and resolution, and have elegant connections to Fourier features and space-filling curves

How are these representations used? The character count manifold and line width manifold are aligned in the residual stream, but get “twisted” by an attention head, to start attending to the previous newline just *before* the end of the current line

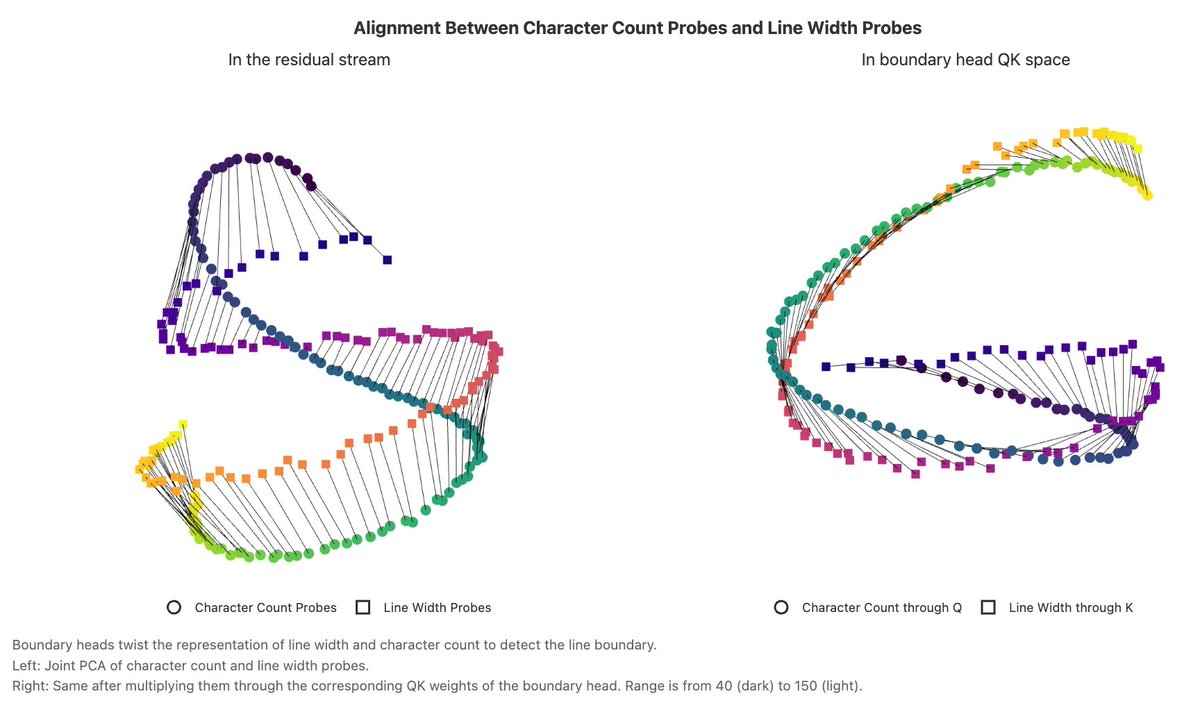
Multiple “boundary heads” twist the manifolds with different offsets. The collective action of these heads computes the number of characters remaining in the line with high precision, loosely akin to stereoscopic vision.

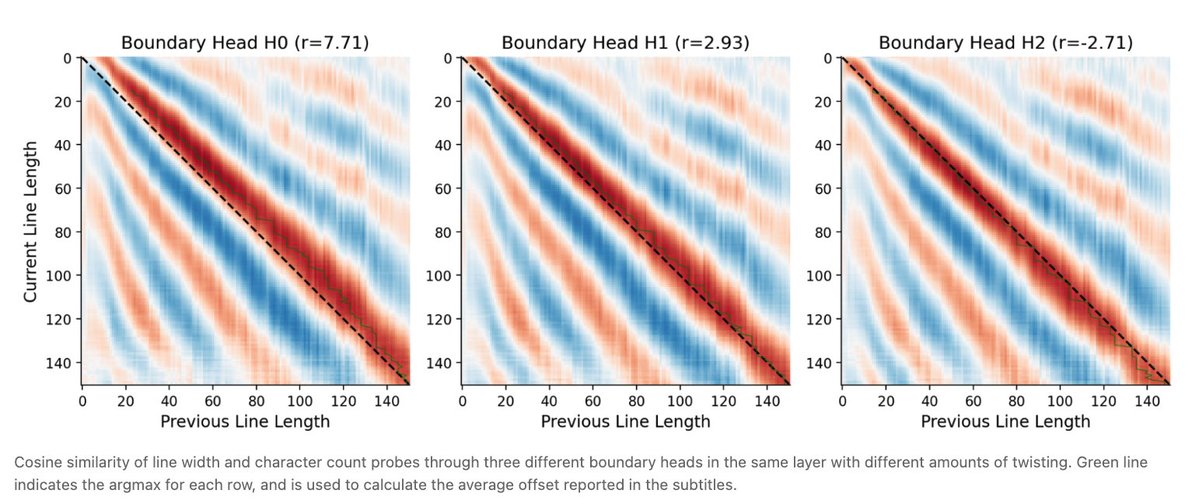
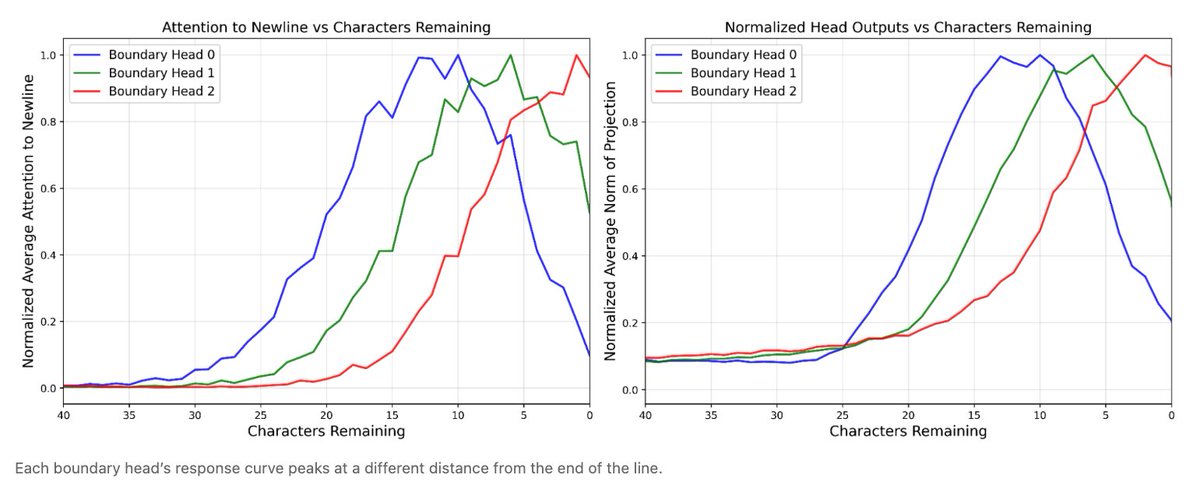
At the end of the model, there is a merging of paths between characters remaining and the next word to determine if it will fit.

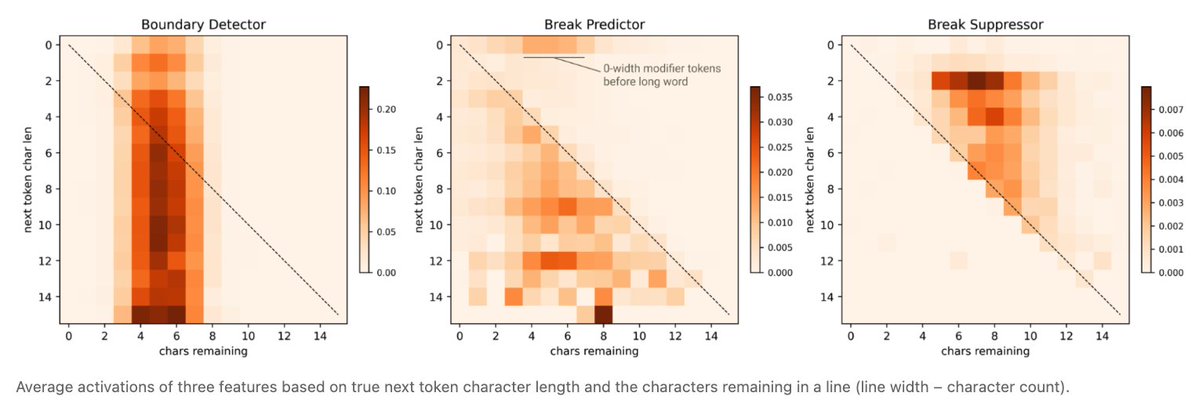
In addition to boundary detector features (which activate irrespective of the next token), there are families of break prediction and break suppressor features which activate if the next word will fit or not!

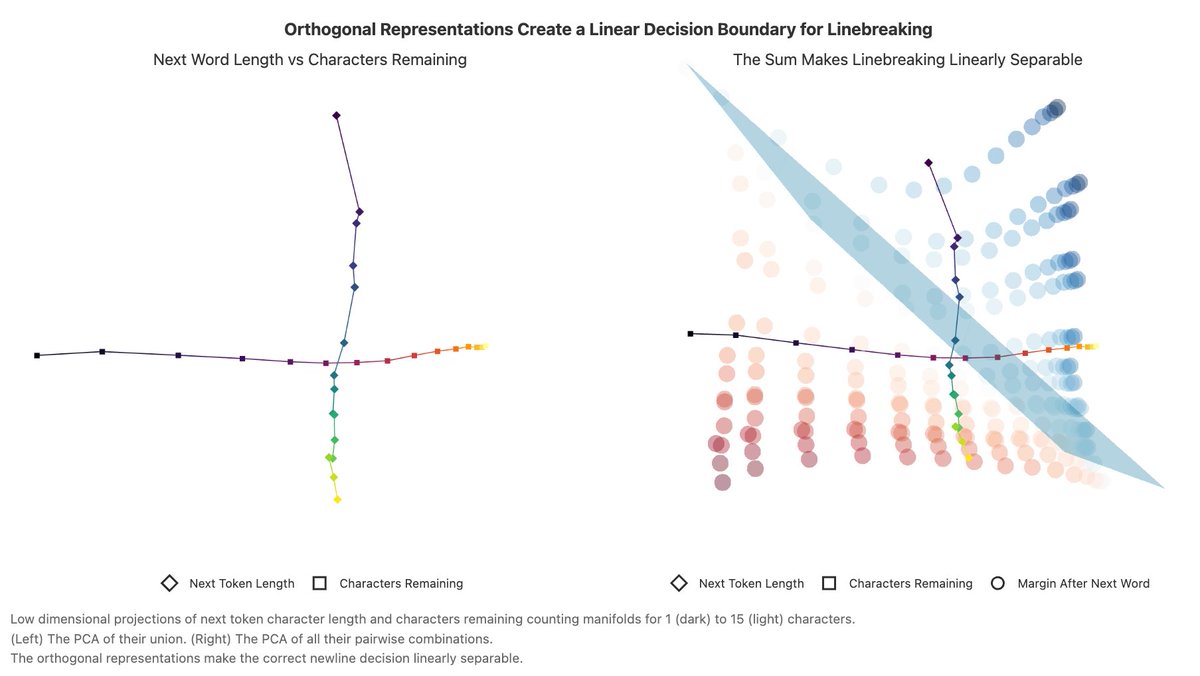
How is this implemented? The model arranges the count of characters remaining and characters in the next word in orthogonal subspaces. This makes the decision to break linearly separable!

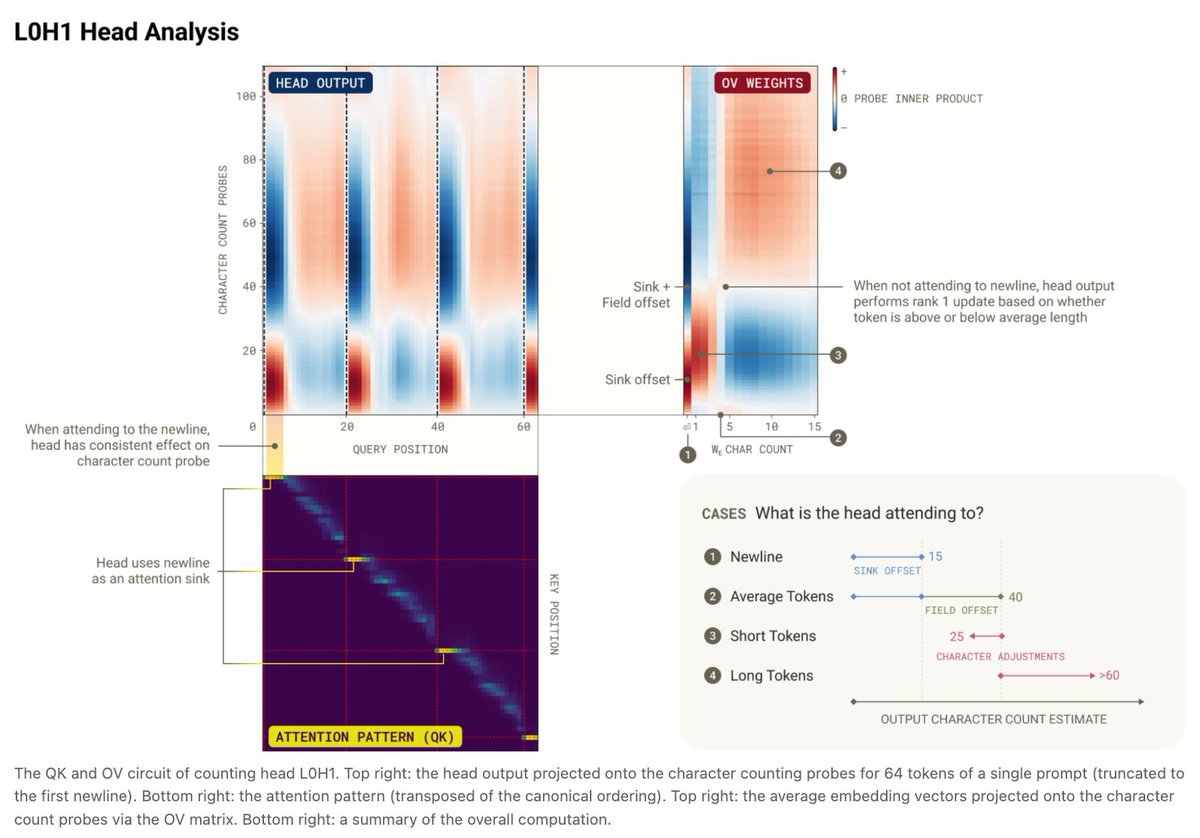
But how did the model compute the character count in the first place? There is a distributed attention algorithm, with at least 11 heads over 2 layers to accumulate the count. Each head “specializes” to contribute a particular part of the count.

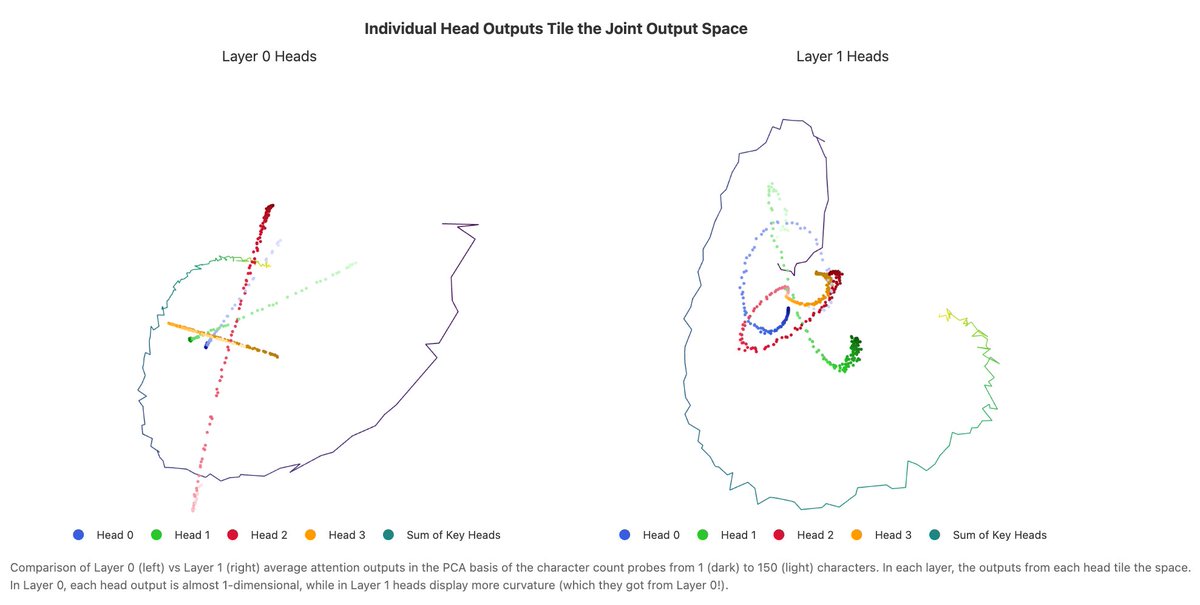
Individually, each head implements a heuristic to convert a token count into a character count followed by a length adjustment. Similar to boundary detection, heads use variable size attention sinks to tile the space, with matching OV weights.

We learned a lot from this project: empirical evidence of previously hypothesized rippled manifolds, the duality of features and geometry, and how features sometimes incur a “complexity tax”. We would be excited about other deep case studies on other naturalistic tasks!

One of the hardest parts of finishing this paper was deciding what to call it! The memes really write themselves… We included some of our favorite rejected titles in the appendix

For full details, you can read the paper here:

Amazing to work with @mlpowered, @ikauvar, @tarngerine, @adamrpearce, @ch402, @thebasepoint!transformer-circuits.pub/2025/linebreak…