Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
Susan Zhang Profile picture
@suchenzang
Nov 21 • 1 tweets • 2 min read • Read on X
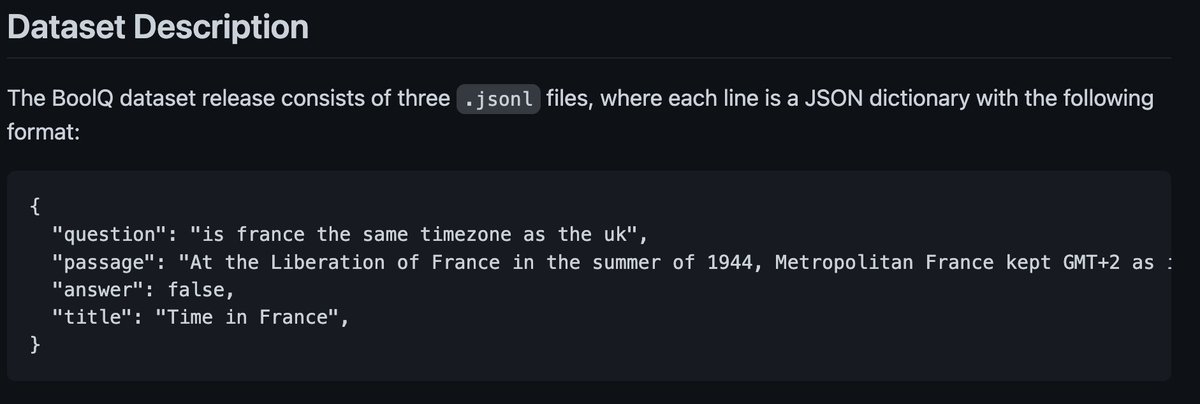
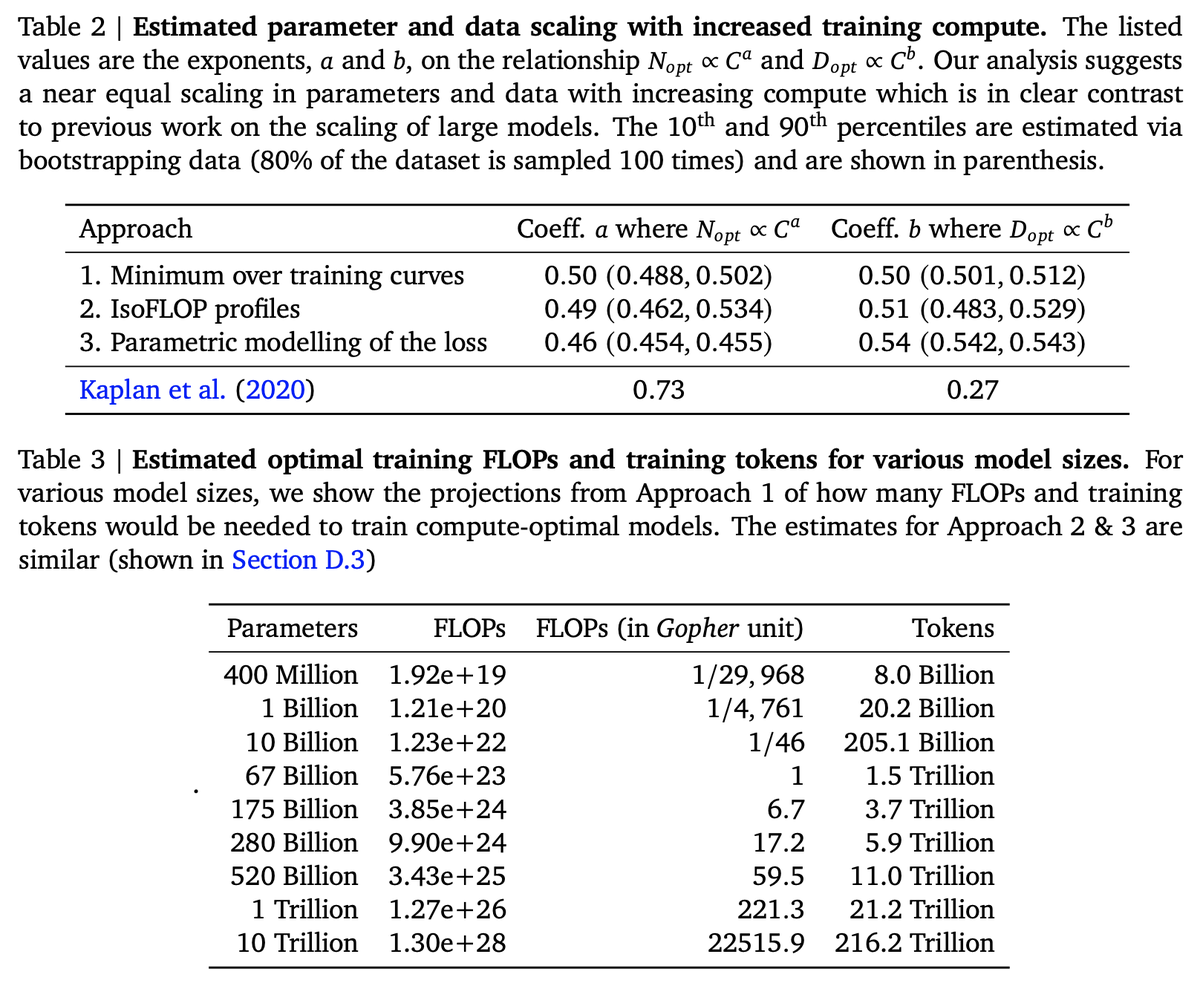
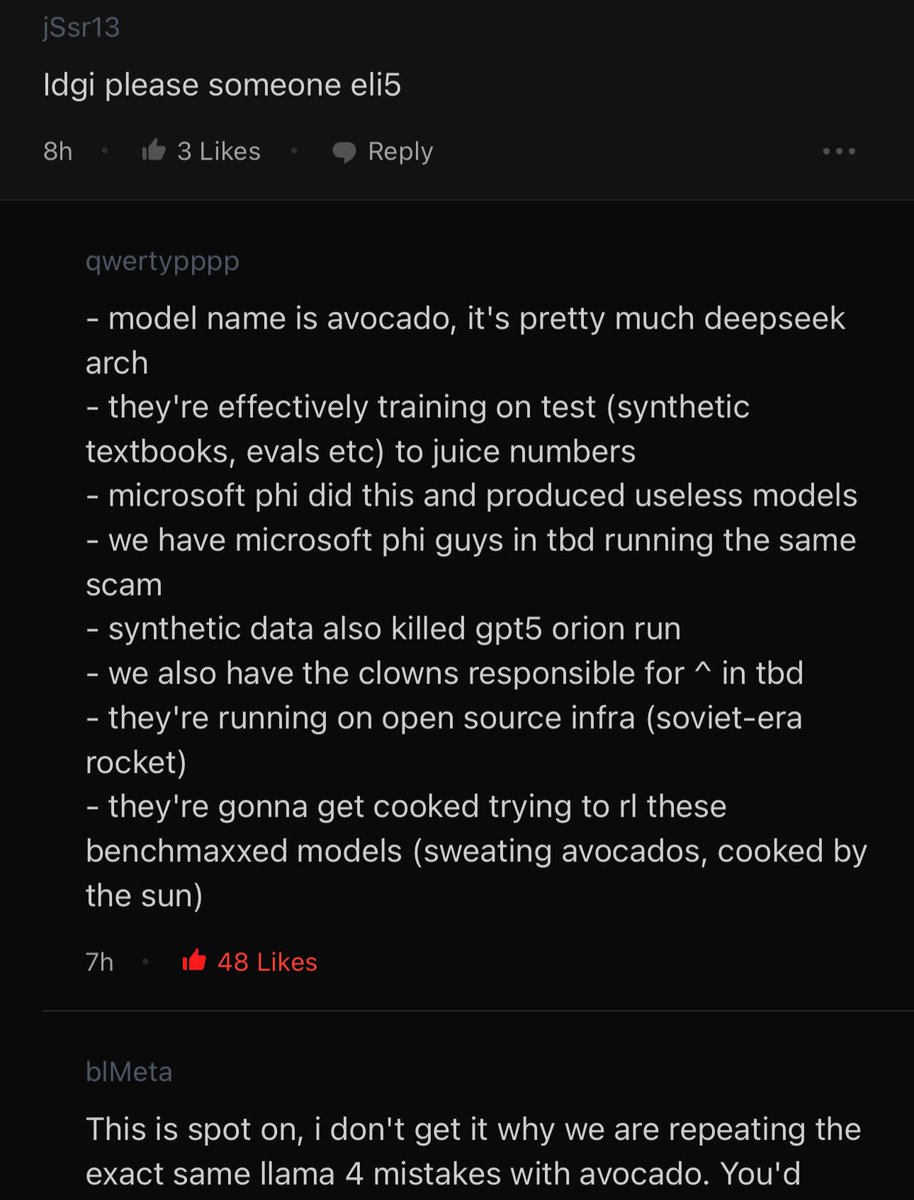
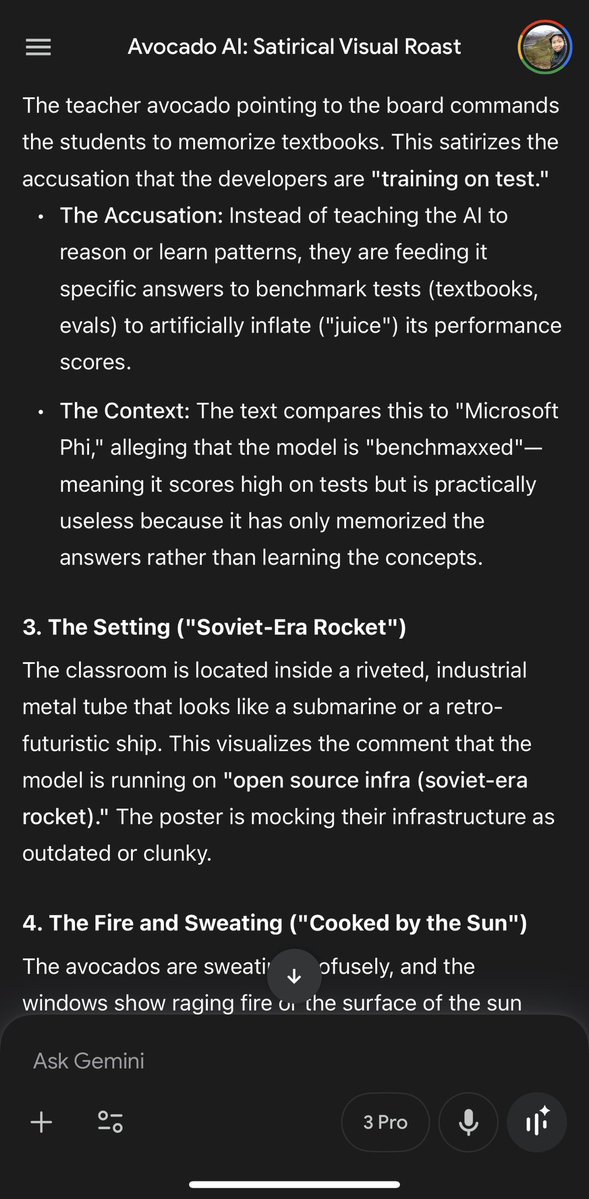
llama5 avocado will be lit Image
Image
Image
Image

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Susan Zhang

Susan Zhang Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @suchenzang

Susan Zhang Profile picture
Jun 9, 2023
There seems to be a high correlation between folks who think "open source LLMs will win" & folks who

1) haven't developed any large-scale infra "in the cloud" themselves

or

2) have never priced out the cost of scaling-out "in the cloud" (for the most powerful models)

1/6
or

3) underestimate the cost of investing in data infrastructure and tooling

(have you seen why Databricks exists?)

2/6
OSS is needed to justify the value of continuing to push the limits of scale (Sutton's bitter lesson) in enabling quick prototypes and demos of possible applications.

But no single software library will solve manual integration glue with existing systems, and...

3/6
Read 6 tweets
Susan Zhang Profile picture
Jan 22, 2023
Piling on to the pile-on (sorry - it's always easy to criticize 😛), here's a rant about benchmarks for LLMs that are used to back claims of "stronger" or "better" models.

Let's start with a tour through GPT-3's Appendix G... 1/8
First up: BoolQ. If you download the actual benchmark, it's true/false completions. GPT-3 swaps in yes/no instead. Why? Well when we did the same swap to yes/no, we saw a +10% accuracy jump on this benchmark.

Wonderful. Clearly on track for a better model already. 2/8 ImageImage
Next up: formatting. Why does CB get prompted for true/false and RTE with True/False?

Why does WebQA use "Q/A", WiC use "question/answer", and ARC use "Question/Answer"?

Could it be... that you simply get better results switching it up? 🤔

It just keeps going... 3/8 ImageImageImageImage
Read 8 tweets
Susan Zhang Profile picture
Jan 21, 2023
After ignoring the details in all these "lets-fit-a-cloud-of-points-to-a-single-line" papers (all likely wrong when you really extrapolate), @stephenroller finally convinced me to work through the math in the Chinchilla paper and as expected, this was a doozy. [1/7]
First thing to make me eye-roll a bit was this fancy equation (4) that seems to re-parameterize the key exponent terms (a,b) into (alpha,beta) to define a coefficient term G. Why this level of indirection just to define a scalar-coefficient? No idea. [2/7]
So then you naturally start wondering what A/B/a/b could be. First stop: (a,b) is set to different values for 3 different "Approaches" in Table 2, each seeming to differ by just a hair: (0.5,0.5) vs (0.49,0.51) vs (0.46,0.54). Ok, sure, why not.

Now for A,B... [3/7]
Read 7 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(