
Machine learning R&D | I make maths/science animations | 𝗧𝗼𝗽 𝘁𝘄𝗲𝗲𝘁𝘀: https://t.co/6gJsSCJ9yK
How to get URL link on X (Twitter) App


 The horizontal axis is the number of dimensions, k. Sample z from a k-dimensional Gaussian with covariance I/k (where I is the k×k identity matrix). The vertical axis shows the probability that the magnitude |z|≤0.95 (blue), |z|>1.05 (green), or in between (orange) 2/
The horizontal axis is the number of dimensions, k. Sample z from a k-dimensional Gaussian with covariance I/k (where I is the k×k identity matrix). The vertical axis shows the probability that the magnitude |z|≤0.95 (blue), |z|>1.05 (green), or in between (orange) 2/ 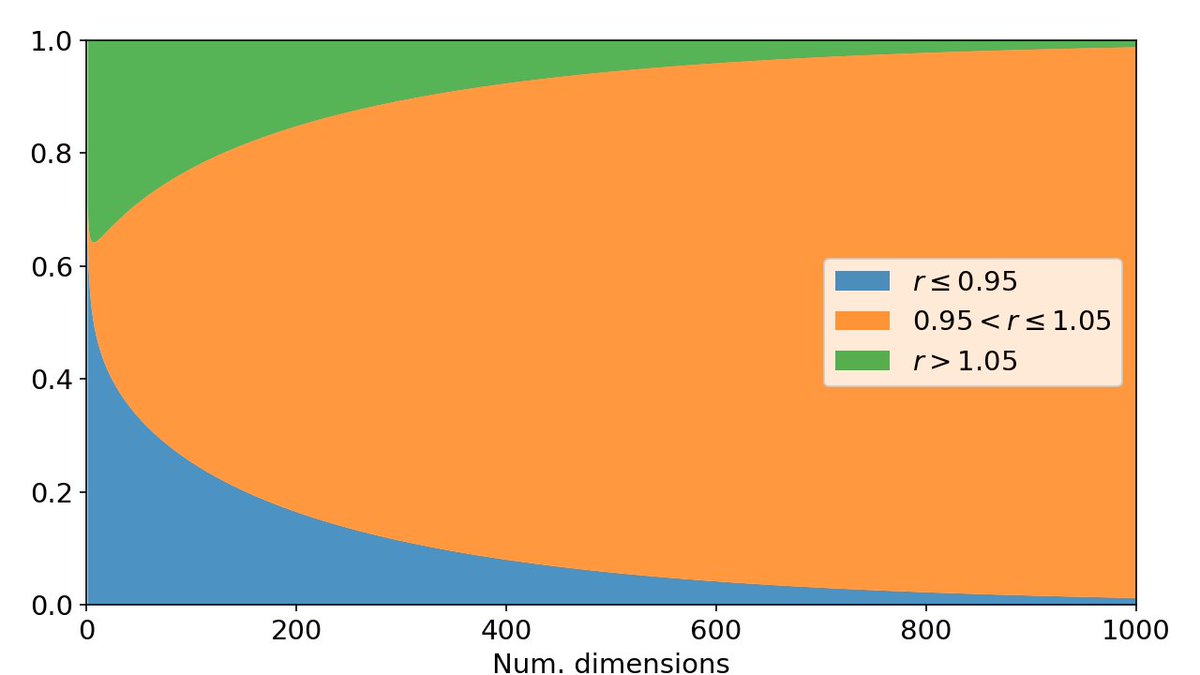

 "The investment in our DNA leads to breakthrough innovation and allows us to move out of the traditional linear system and into the future." 2/
"The investment in our DNA leads to breakthrough innovation and allows us to move out of the traditional linear system and into the future." 2/ 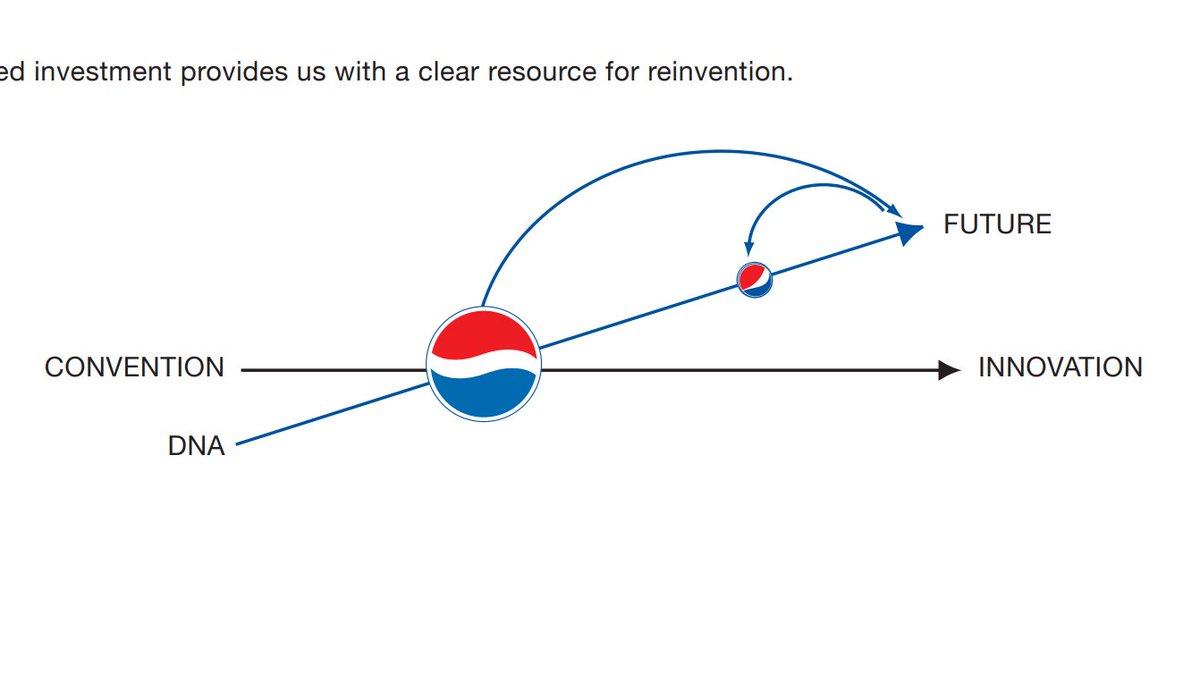

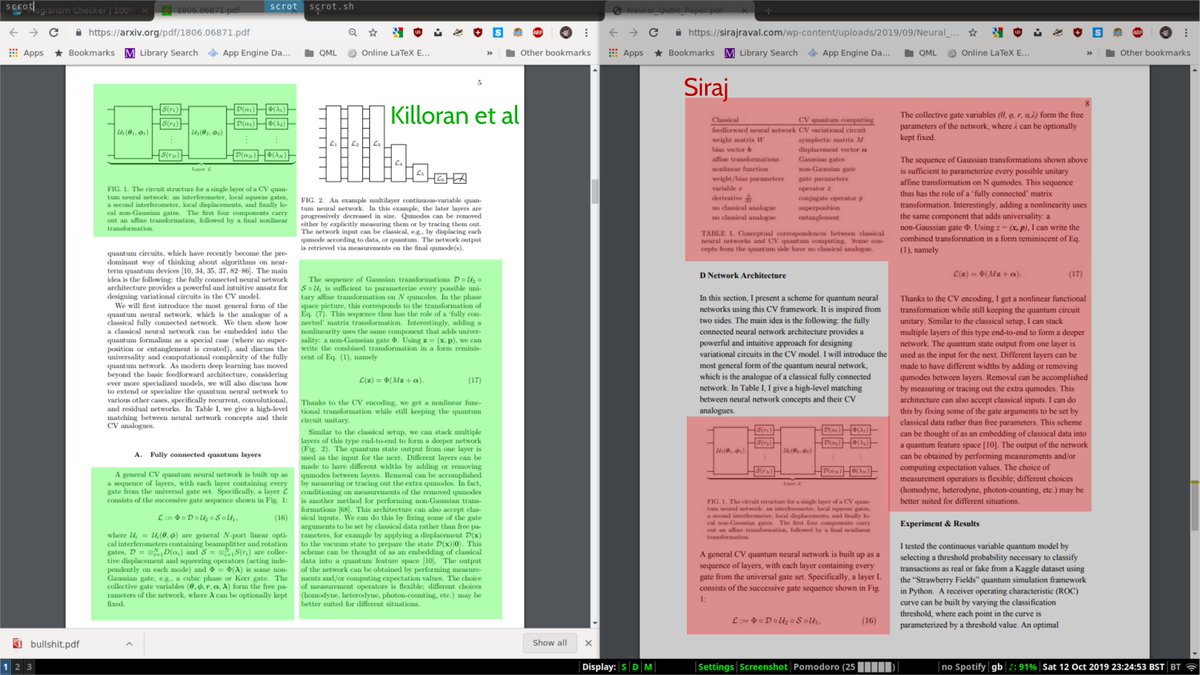

 @sirajraval He cites Killoran et al. in the abstract only, and says he presents a model "similar to" it, but the shown parts are almost word for word the same, and the figure, table, and captions are also lifted
@sirajraval He cites Killoran et al. in the abstract only, and says he presents a model "similar to" it, but the shown parts are almost word for word the same, and the figure, table, and captions are also lifted
https://twitter.com/AndrewM_Webb/status/11762040008212029452/ A thread on Penrose tilings
https://twitter.com/AndrewM_Webb/status/1178581247880257543


