For your enjoyment, here is the reading list for my undergraduate core seminar this semester in Philosophy, Science, and Mathematics. We shall focus on topics in the philosophy of mathematics, philosophy of science, and philosophy of computability and AI. We shall read several selections from my book, Lectures on the Philosophy of Mathematics, MIT Press 2020.
mitpress.mit.edu/9780262542234/…

Here is the list of challenge questions I asked the audience at my talk yesterday at the Fudan Logic Seminar on the surreal numbers.
Can you answer? Post your solutions in response to each question separately. 1. How many disjoint unit intervals fit in the interval [0,ω] in the surreal line?

On the cultural differences between math and philosophy in regard to Q & A after a seminar or colloquium talk. A thread. Please feel free to comment. 🧵 Philosophy
Philosophers typically have extended Q & A after a talk, often as long or even longer than the talk itself. A standard format would have a one hour talk or 50 minutes, perhaps a short break of 5 minutes, and then another hour or 50 minutes of questions and discussion. Another more compressed standard format calls for a 20 minute talk and 40 minutes of Q & A. In truth, there is never enough time—at almost every talk, more people want to ask questions or contribute to the Q & A discussion than is possible, and it is common for the moderator to announce that time is up, alas, even though many people still remain on the list to ask questions. At conferences, many talks are arranged into small sessions with a main speaker and then several commentators who give talks criticizing the main talk, and then rebuttals and then Q & A with that panel but also eventually audience participation.

Take my Philosophy of Mathematics final exam!
Post your answers in response to each question. What is logicism? Which philosophers are associated with this philosophical project? What were the central ideas and major issues or developments arising in connection with this program? Was the program ultimately realized successfully?

An imaginary mathematical history.🧵
I should like to sketch an imaginary mathematical history, an alternative history by which the continuum hypothesis (CH) might have come naturally to be seen as a core axiom of set theory and one furthermore necessary for ordinary mathematics. Let us imagine that in the early days of calculus, the theory was founded upon infinitesimals, but in a clear manner that identified the fundamental principles relating the real field ℝ to the hyperreals ℝ*, identifying the transfer principle and saturation.

Three variations on Tarski.
Let me present three variations of Tarski's theorem on the non-definablity of truth. The first is proved in Gödelian style using Gödelian methods; the second is Russellian; and the last is purely Cantorian. But all express the nondefinability of truth. First, the sentential variation, in Gödelian style. Truth is not definable, in the sense that there is no arithmetically expressible formula T(x) such that T('σ')⟷σ for every arithmetic sentence σ.

The countable random graph.
I realized something today about the countable random graph. Namely, although this graph is highly homogeneous and has numerous automorphisms, it is nevertheless definably rigid, meaning that it has no definable automorphisms. Let me explain. The countable random graph arises from a countable set of vertices by flipping independent fair coins to determine whether there is an edge between any two nodes.

Consider several structures on the natural numbers:
• Successor ⟨ℕ,0,S⟩
• Order ⟨ℕ,0,<⟩
• Addition ⟨ℕ,0,+⟩
What I claim is that each structure is definable in the next, but not conversely. The positive claim is easy, for we can easily define the successor function from the order—the successor Sx is simply the least element that is larger than x. And similarly, we can define the order from +, since
x < y if and only if ∃z (z≠0 and x+z = y).

Truth and provability, a thread. Let us compare Tarski's theorem on the nondefinability of truth with Gödel's incompleteness theorem. Smullyan advanced the view that much of the fascination with Gödel's theorem should be better directed toward Tarski's theorem. Both theorems begin with the profound arithmetization idea, Gödel's realization that arithmetic interprets essentially any finite combinatorial process, including arithmetic syntax itself. Every arithmetic assertion φ is thus represented in arithmetic by Gödel code 'φ', a number.

I once saw an incredible lecture in Berkeley by a historian of science, one of the best talks I have ever seen. He started his talk sitting on the desk amongst a huge pile of physics textbooks from history, each in its day "the best textbook of its time." He began by showing us the text written by a student of Isaac Newton, which explained Newtonian forces and the motion of planets. Nevertheless, it had various mistakes and misunderstandings. He set it aside and moved to the next book, also excellent, but also flawed in some way.

Foreshadowing — the algebra of orders. Here is an addition table for some simple finite orders. Did you know that you can add and multiply any two orders? A+B means a copy of A with a copy of B above. Stay tuned for multiplication... I expanded the addition table.

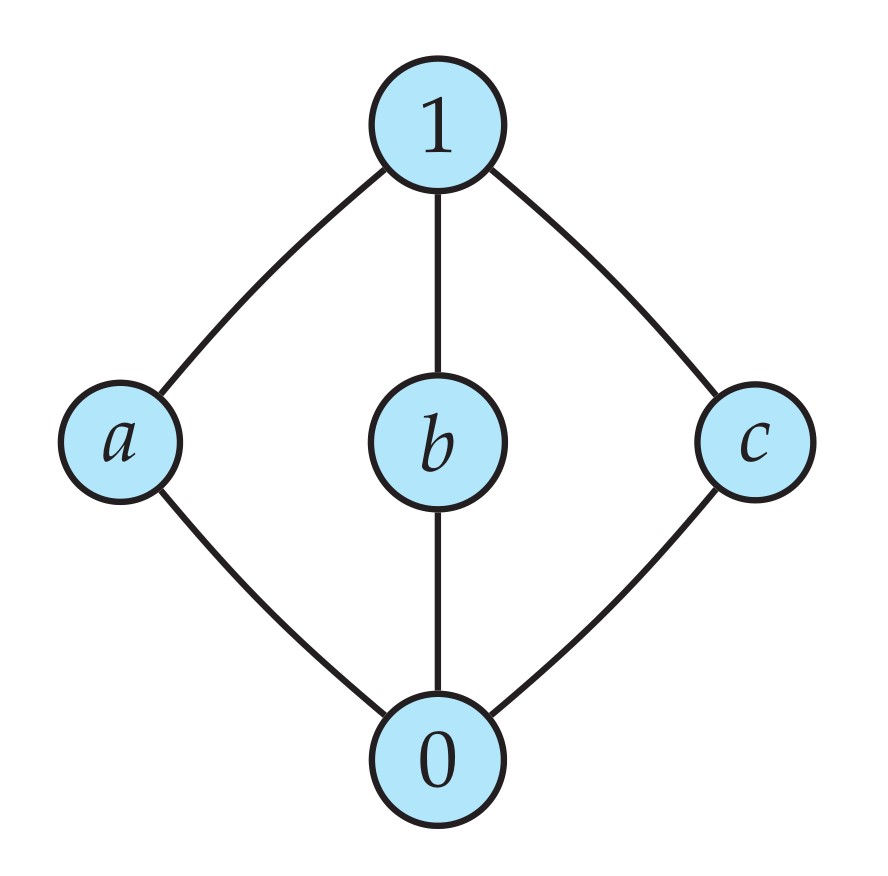
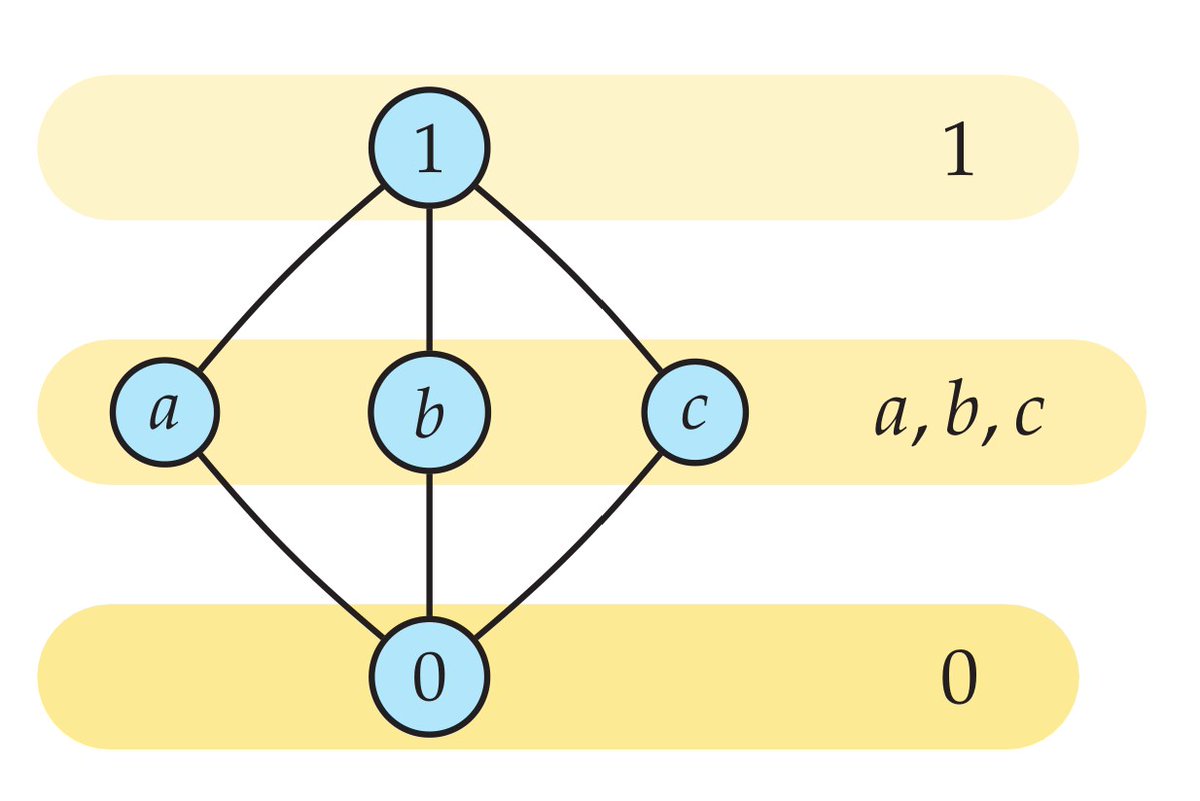Order relations are often fruitfully conceived as being stratified into a linear hierarchy of levels. The simple order shown here, for example, is naturally stratified by three levels. What is a "level"? A stratification of an order into levels amounts to a linear preorder relation on the same domain. namely, a linear grading of a partial order ≼ is a preorder relation ≤ respecting the strict relation, that is, for which a≺b implies a<b.

Let me share some illustrations I've recently created to discuss the topic:

What is a number?

Two sets are equinumerous—they have the
same cardinal size—when they can be placed into a one-to-one correspondence, like the shepherd counting his sheep off on his fingers. Hume's principle asserts that the numbers of F's is the same as the number of G's just in case these classes are equinumerous.

{ x | Fx } ~ { x | Gx }

The equinumerosity relation thus partitions the collection of all sets into equinumerosity classes of same-size sets.