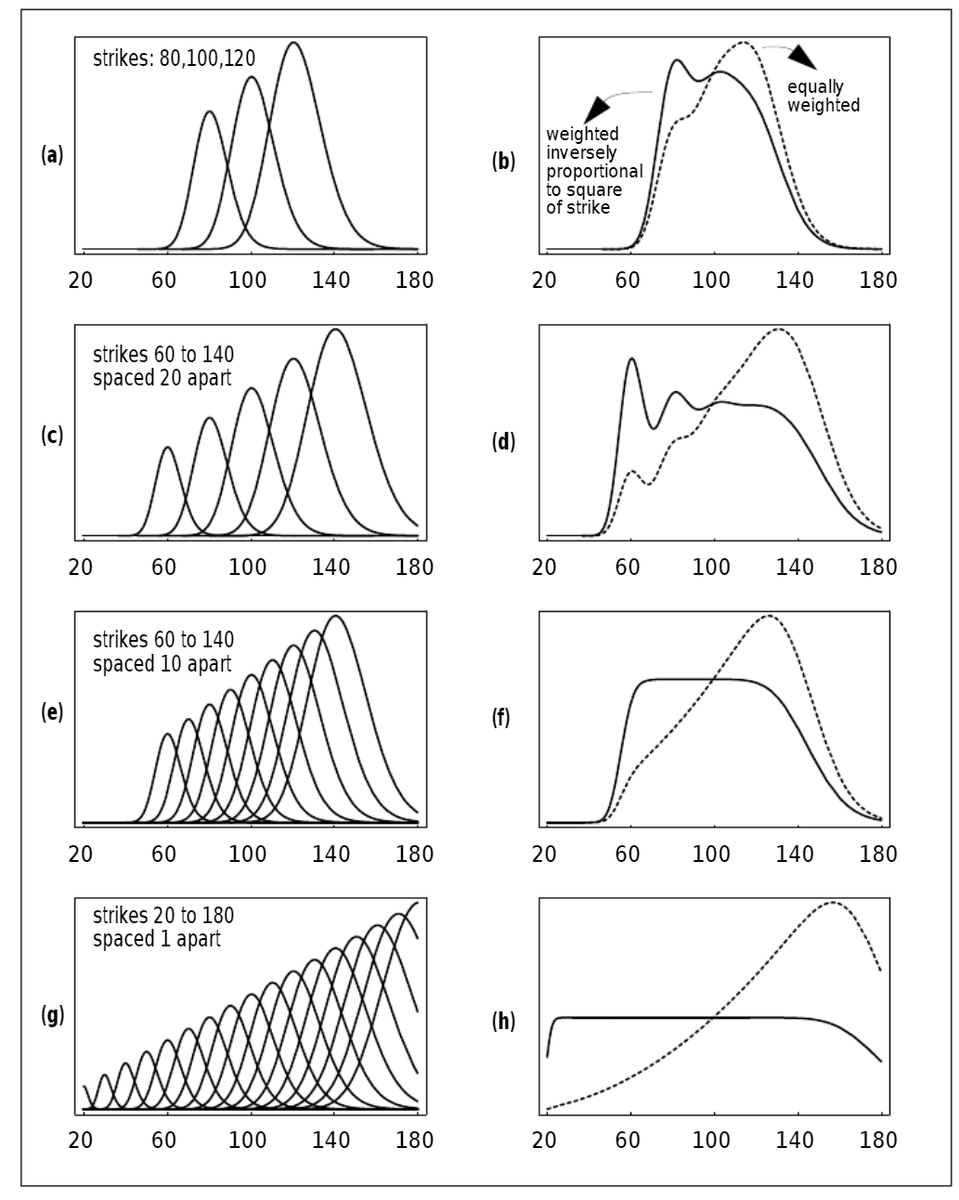
How to get URL link on X (Twitter) App






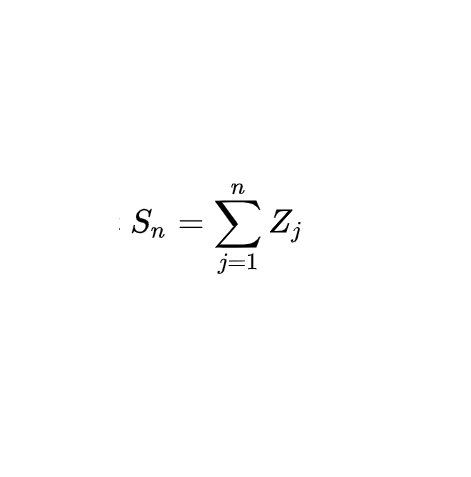
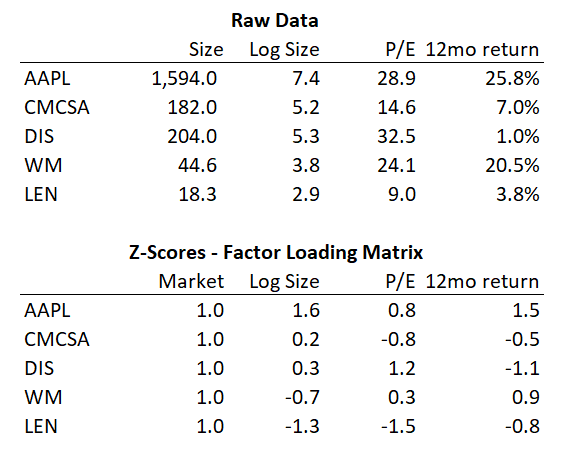
https://twitter.com/ONAN_OUS/status/1278722283519873024The main thing is we want a closed-form way to calculate factor exposures and the returns of those factors. We first start by defining our factors and their metrics.
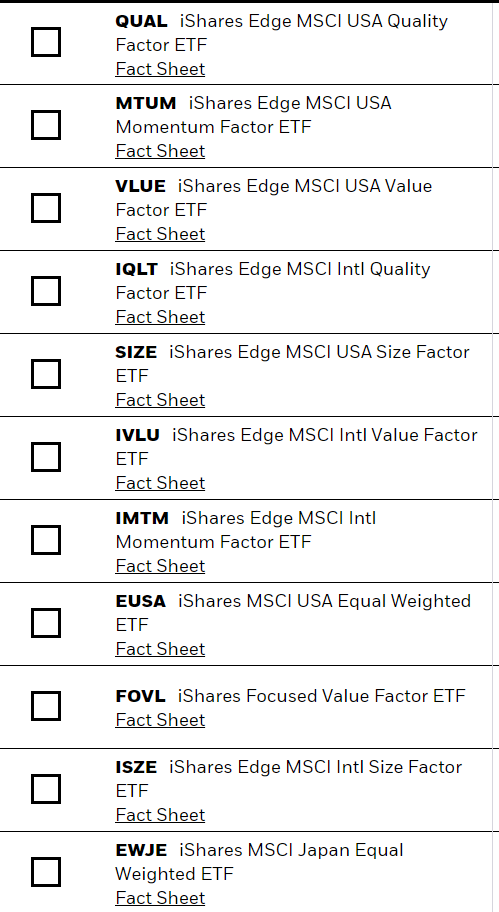
https://twitter.com/ONAN_OUS/status/1278719269996425216The push to bring these into practice was done at Goldman Sachs Asset Management. @CliffordAsness started there in 1994, and left to create AQR in 1998. Mark Carhart ran the Global Alpha fund at GSAM until about 2010 and left to launch Kepos with Bob Litterman, another GSAM alum.