
How to get URL link on X (Twitter) App

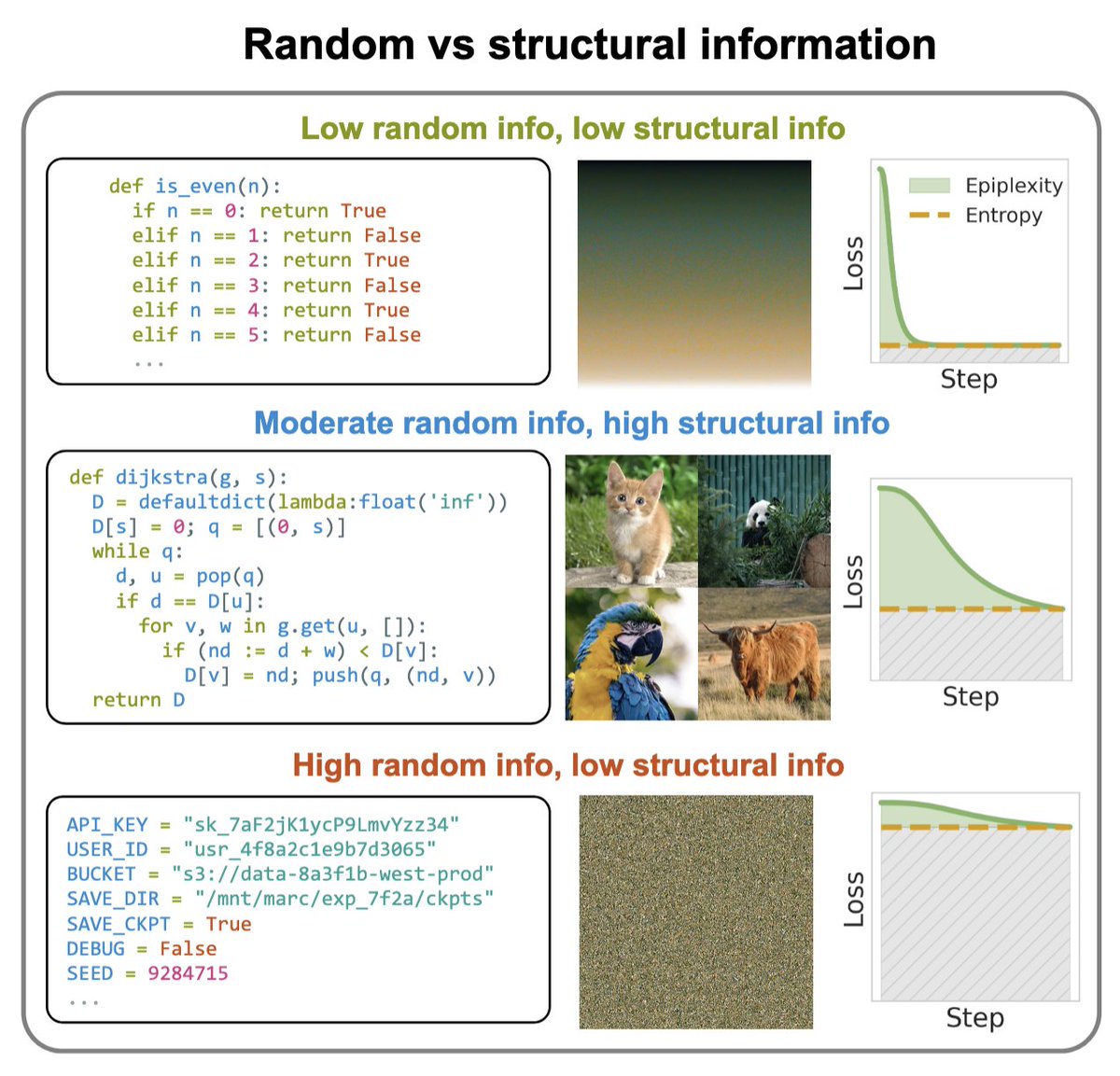
https://twitter.com/m_finzi/status/2008934727156453661Information theory comes up empty-handed on key questions: can we learn more from data than existed in the generating process? Can new information be created from deterministic transformations? Can the learnable content in data be evaluated for broad generalization? 2/7

 What makes deep learning different? Not overparametrization, benign overfitting, or double descent, which can be reproduced with other models and explained with old generalization frameworks. Understanding DL doesn't require rethinking generalization -- and it never did! 2/12
What makes deep learning different? Not overparametrization, benign overfitting, or double descent, which can be reproduced with other models and explained with old generalization frameworks. Understanding DL doesn't require rethinking generalization -- and it never did! 2/12
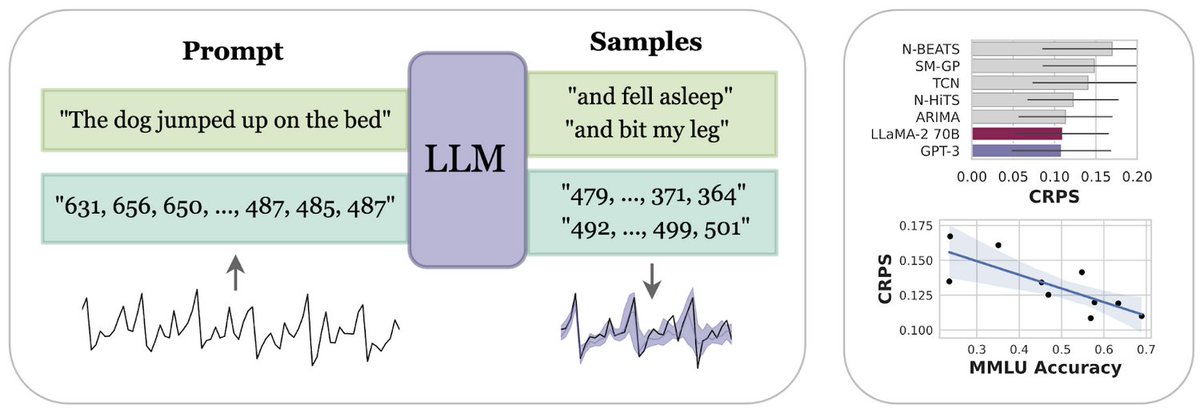
 Naively using LLMs like GPT-3 for time series extrapolation can fail out of the box because of suboptimal tokenization and preprocessing. We show that if we tokenize numbers to individual digits, LLMs really shine!
Naively using LLMs like GPT-3 for time series extrapolation can fail out of the box because of suboptimal tokenization and preprocessing. We show that if we tokenize numbers to individual digits, LLMs really shine!

https://twitter.com/LotfiSanae/status/1549764850703892481To recap, the marginal likelihood answers the question "how likely is my prior to generate the training data?" which is fundamentally different than "will my trained model provide good generalization?", leading to many discrepancies. See
https://twitter.com/andrewgwils/status/1496663760131563524?s=20
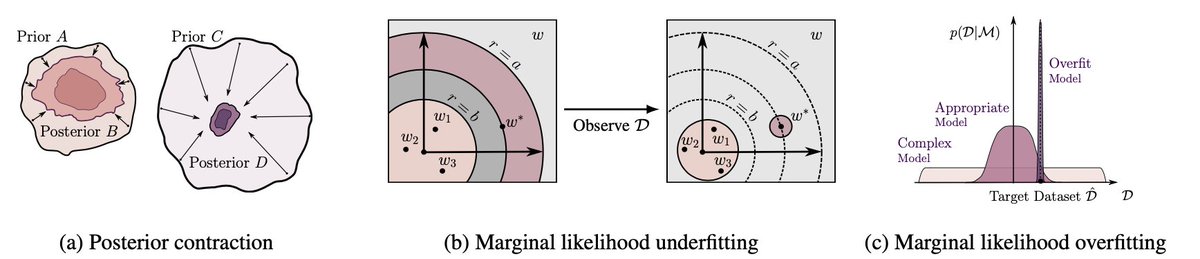
 The search for scientific truth is elusive. How do we select between theories which are entirely consistent with any data we observe? The marginal likelihood p(D|M) -- the probability we would generate our observations from our prior model -- provides a compelling approach. 2/23
The search for scientific truth is elusive. How do we select between theories which are entirely consistent with any data we observe? The marginal likelihood p(D|M) -- the probability we would generate our observations from our prior model -- provides a compelling approach. 2/23

https://twitter.com/Pavel_Izmailov/status/1407522681516331016
 Suppose for instance there are dead pixels in an image. The weights attached to these pixels don’t affect the predictions, and so MAP (regularized optimization) drives them to zero. A BMA instead samples these weights from the prior... 2/5
Suppose for instance there are dead pixels in an image. The weights attached to these pixels don’t affect the predictions, and so MAP (regularized optimization) drives them to zero. A BMA instead samples these weights from the prior... 2/5


 We decouple our understanding of good fidelity --- high student teacher agreement --- from good student generalization. 2/10
We decouple our understanding of good fidelity --- high student teacher agreement --- from good student generalization. 2/10 

https://twitter.com/dabeaz/status/1398625259708993538From a probabilistic perspective, whether we are doing supervised, semi-supervised, or unsupervised learning, forming our training objective involves starting with an observation model, turning it into a likelihood, introducing a prior, and then taking our log posterior. 2/8

 We show that Bayesian neural networks reassuringly provide good generalization, outperforming deep ensembles, standard training, and many approximate inference procedures, even with a single chain. 2/10
We show that Bayesian neural networks reassuringly provide good generalization, outperforming deep ensembles, standard training, and many approximate inference procedures, even with a single chain. 2/10 

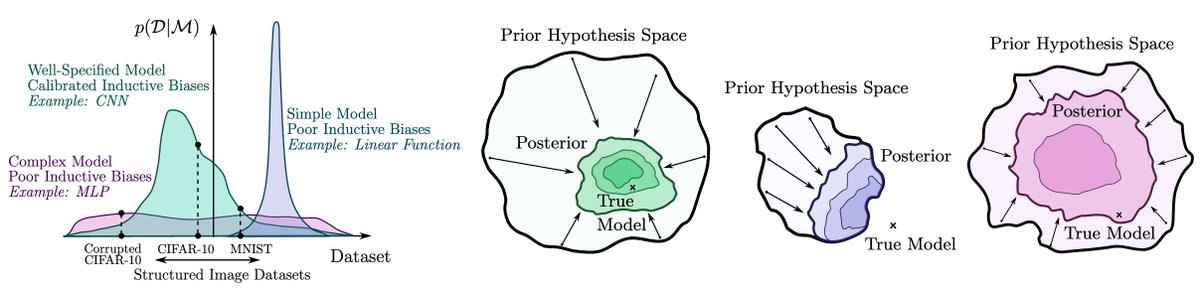
 The deep image prior shows this p(f(x)) captures low-level image statistics useful for image denoising, super-resolution, and inpainting. The rethinking generalization paper shows pre-processing data with a randomly initialized CNN can dramatically boost performance. 2/15
The deep image prior shows this p(f(x)) captures low-level image statistics useful for image denoising, super-resolution, and inpainting. The rethinking generalization paper shows pre-processing data with a randomly initialized CNN can dramatically boost performance. 2/15 

 ...to form a model average, via simple Monte Carlo. But if we instead directly consider what we ultimately want to compute, the integral corresponding to the marginal predictive distribution (the predictive distribution not conditioning on weights)... 2/10
...to form a model average, via simple Monte Carlo. But if we instead directly consider what we ultimately want to compute, the integral corresponding to the marginal predictive distribution (the predictive distribution not conditioning on weights)... 2/10

 Complex dynamics can be described more simply with higher levels of abstraction. For example, a trajectory can be found by solving a differential equation. The differential equation can in turn be derived by a simpler Hamiltonian or Lagrangian, which is easier to model. 2/5
Complex dynamics can be described more simply with higher levels of abstraction. For example, a trajectory can be found by solving a differential equation. The differential equation can in turn be derived by a simpler Hamiltonian or Lagrangian, which is easier to model. 2/5 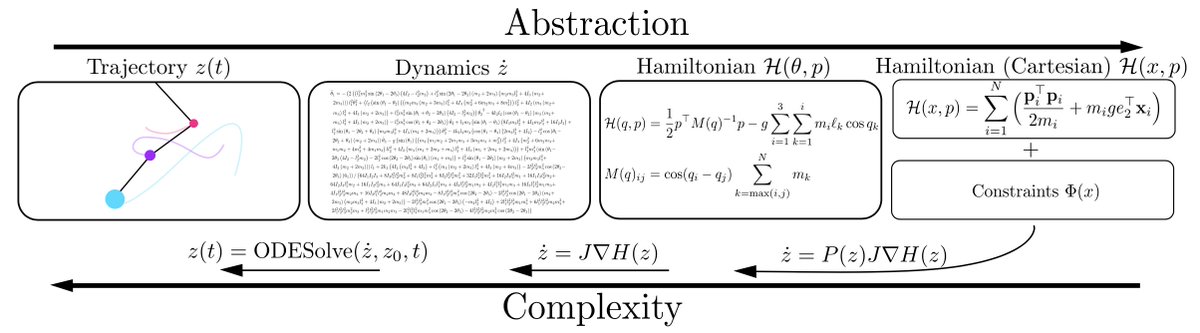
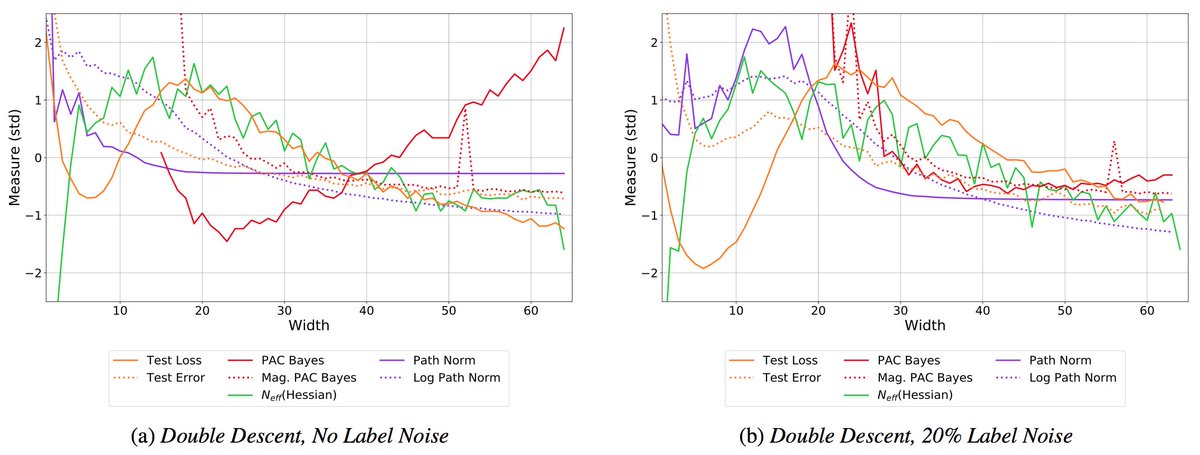

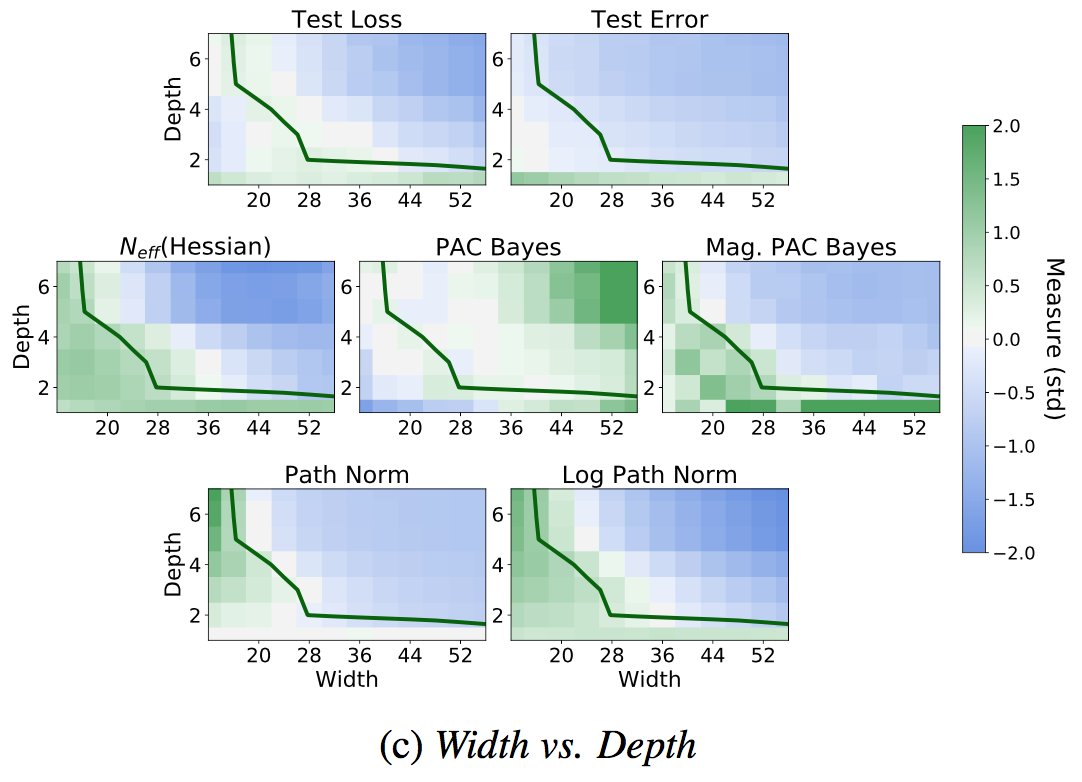 The plots are most interpretable for comparing models of similar train loss (e.g. above the green partition). N_eff(Hess) = effective dimension of the Hessian at convergence. 2/16
The plots are most interpretable for comparing models of similar train loss (e.g. above the green partition). N_eff(Hess) = effective dimension of the Hessian at convergence. 2/16
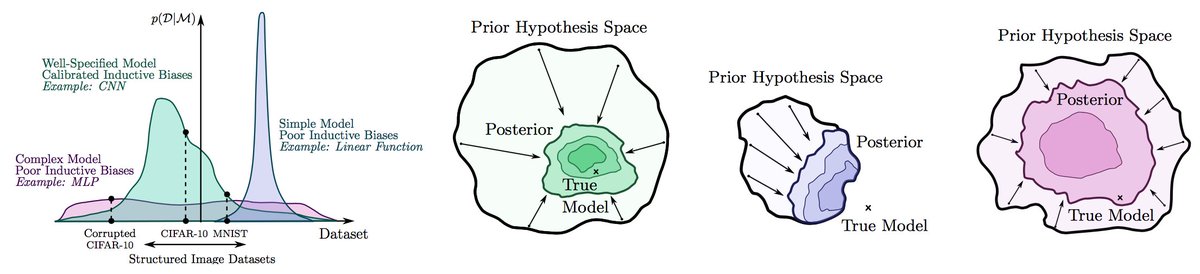
 Since neural nets can fit images with noisy labels, it has been suggested we should rethink generalization. But this behaviour is understandable from a probabilistic perspective: we want to support any possible solution, but also have good inductive biases. 2/19
Since neural nets can fit images with noisy labels, it has been suggested we should rethink generalization. But this behaviour is understandable from a probabilistic perspective: we want to support any possible solution, but also have good inductive biases. 2/19
https://twitter.com/carlesgelada/status/1208618401729568768In particular, the predictive distribution we often want to find is p(y|x,D) = \int p(y|x,w) p(w|D) dw. 'y' is an output, 'x' an input, 'w' the weights, and D the data. This is not a controversial equation, it is simply the sum and product rules of probability. 2/18