The Dirac Delta "Function" 𝛿(x) is a 𝐆𝐞𝐧𝐞𝐫𝐚𝐥𝐢𝐳𝐞𝐝 𝐃𝐢𝐬𝐭𝐫𝐢𝐛𝐮𝐭𝐢𝐨𝐧 that comes up a lot in physics—specifically in integrals.

When a function ƒ is integrated with 𝛿(x - a), the Dirac Delta picks out the value at ƒ(a).

Moreover, integrating 𝛿(x) gives 1. We call 𝛿(x) a “𝐆𝐞𝐧𝐞𝐫𝐚𝐥𝐢𝐳𝐞𝐝 𝐃𝐢𝐬𝐭𝐫𝐢𝐛𝐮𝐭𝐢𝐨𝐧” because it’s defined as the general limit of functions that integrate to 1 over infinite bounds.

For example, a normalized gaussian or sinc function will satisfy the above.

Don't quite get it? Don't worry. 👉🏾

1/15) What is the Hamiltonian? And why is it so special? Most importantly, how does it relate to Lagrangian mechanics and give us equations of motion?

This is a thread on how H, the Hamiltonian can tell you the same story as L, the Lagrangian.

[Warning: Technical thread] 2/ Here's an earlier thread I wrote on the Principle of Least Action and the Euler-Lagrange equations. Check it out, if you'd like to catch up!

https://twitter.com/astroparticular/status/1152676730311569409

You’ve heard that two matrices multiply into another matrix, but with two 𝑡𝑒𝑛𝑠𝑜𝑟𝑠, two “matrices” can multiply to become a scalar.

Heck yes, this is a (short) thread on✨ 𝑡𝑒𝑛𝑠𝑜𝑟𝑠 ✨ At first, you *can* think of tensors as multi-dimensional arrays—-but there’s more to them than that.

Here’s an earlier thread I wrote if you want to catch up!

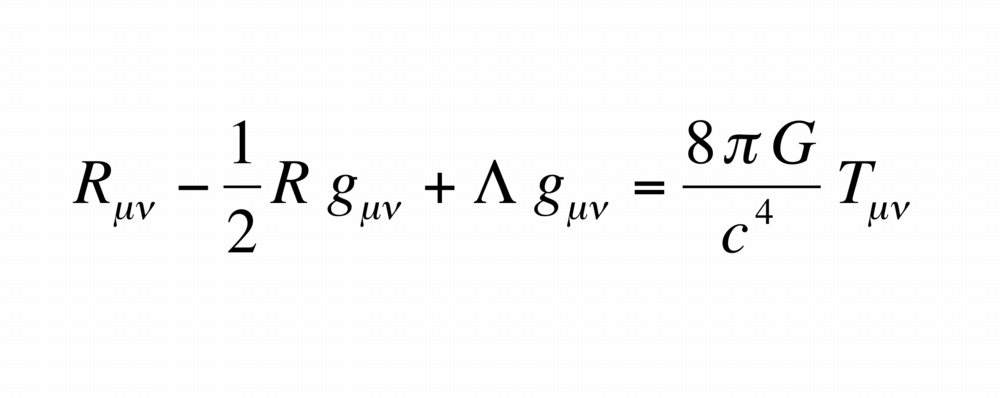
https://twitter.com/astroparticular/status/1154089773344030720?s=20

1/ The Einstein Energy-Momentum Relation can be straightforwardly turned into the `Klein-Gordon Equation.` ✍🏽

Why’s that important?

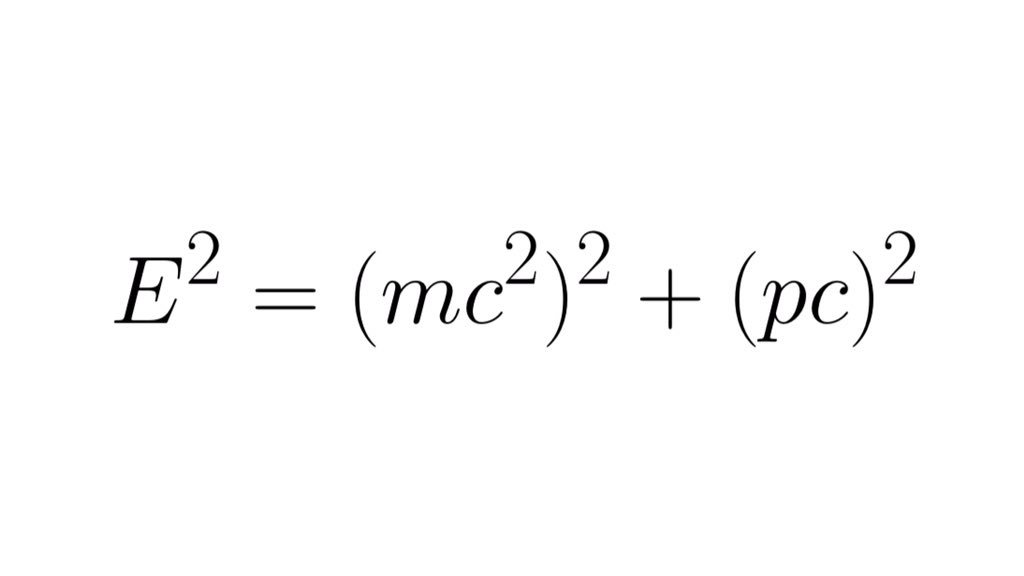
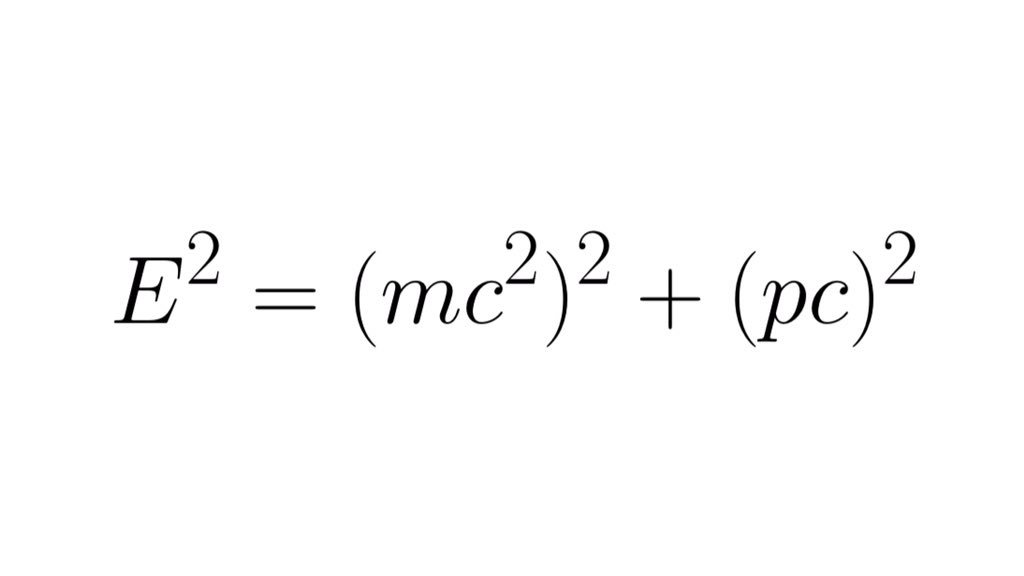The KG-Equation describes spinless particles of any charge! † 2/ If you use natural units (author’s note: ❤️) where ℏ = c = 1, and replace `E` and `p` for their quantum operators... ➡️

If you know about matrices, you already kind of know about tensors. Tensors are a very powerful way of packaging equations together through their operations.

Let's learn more!
[1/3] Tensor can be categorized by rank, i.e. how many "rows and columns they have."

Rank 0: Scalar/Number
Rank 1: Vector
Rank 2: NxN matrix
Rank >= 3: Tensor

I did a visualization of these ranks below, and I kind of cheated in drawing a "4D-tensor" but hey, can you blame me?
[2/3]

🎥 Ready, set, ACTION!

Here's a still from one of my favorite movies ever: Interstellar. But what is Murphy writing on the board? What does this equation mean?

Luckily, this gives me a reason to talk about one of my favorite concepts in physics: the principle of least action! Instead of looking at Murphy's really complex (ten dimensional action), let's look at a simpler version.

This equation below is the definition of action.

Let's pick it apart together and understand why it's so powerful. 💪🏽