In 1958 Roger Penrose and his father Lionel presented the following interesting "room." The curved walls bounding this room are mirrored, yet a light source placed anywhere in region A will leave region B dark, and vice versa.
1/4 The essential feature is that the top curve is half an ellipse with focal points at Q and R. (The shapes of the walls bounding A and B are unimportant.) The geometry of the ellipse guarantees that light rays from A [or B] will reflect off the ellipse and return to A [B].
2/4

Topological magic trick: Draw a rectangular border around a piece of paper. Tell the audience member that they will be drawing a simple closed curve on the paper—the more complicated they make it, the better. It can (and should) go in and out of the border rectangle
1/11 repeatedly. Inform them that "simple" means that it can't intersect itself and "closed" means it ends where it begins. Draw the first little bit of the curve to show them what you have in mind. Next, turn your back and have them draw the rest of the curve so you can't see
2/11

A pile of granular material has a maximum slope on its side. This is known as the "angle of repose." I measured the angle of repose of ordinary table salt to be about 33.5°. By pouring salt on raised shapes you can obtain interesting geometric patterns. 1/5 For instance, pour it on a polygon and it bisects each angle. So when we pour salt on a triangle we obtain a pyramid in which the peak sits above the incenter of the triangle! 2/5

Here's a great card trick that is easy to perform and will ("probably") amaze your friends. Shuffle a deck of cards. Have your friend draw a card and look at it without showing it to you. In the example below, let's say it is the first card, the 10 of spades. Now, slowly deal out the rest of the deck face up into a pile. Your friend counts off in her head (silently) the number on her card (or spells the card if it is a face card, like K-I-N-G). When she gets to her number, that becomes her new card (the ace of diamonds in the deck above). She

It's common to hear the following facts about Klein bottles:
1) To avoid self-intersections, it must live in at least 4-dimensional space.
2) Like a Möbius band, it's a one-sided surface.
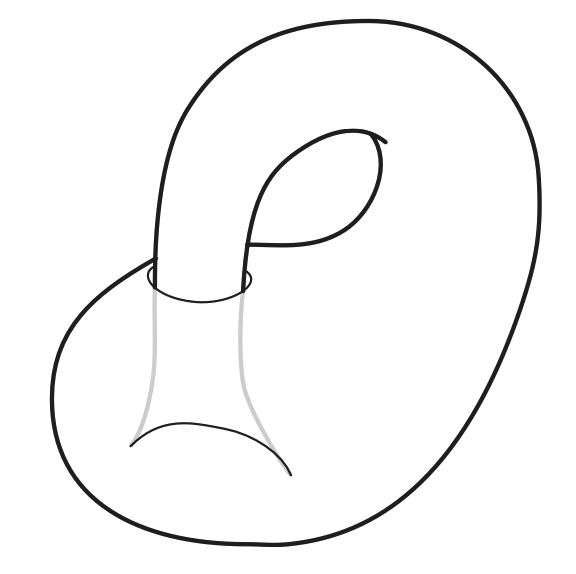
The problem is, a Klein bottle living in 4-dimensional space is NOT one-sided! Why not? 1/13 The familiar picture of a Klein bottle is (using technical language) an "immersion" in 3-dimensional space. Everything is fine except where the bottle passes through itself—it intersects itself along a circle. In this immersion, it is not hard to see why it is called 2/13

A topological magic trick.

(Mathematical explanation in the next tweet.) When joined, the rubber band and carabiners are topologically equivalent to the Borromean rings—an elementary configuration of three unknotted circles that are linked but no two are linked to each other. Clipping the carabiners changes a crossing making them all unlinked.

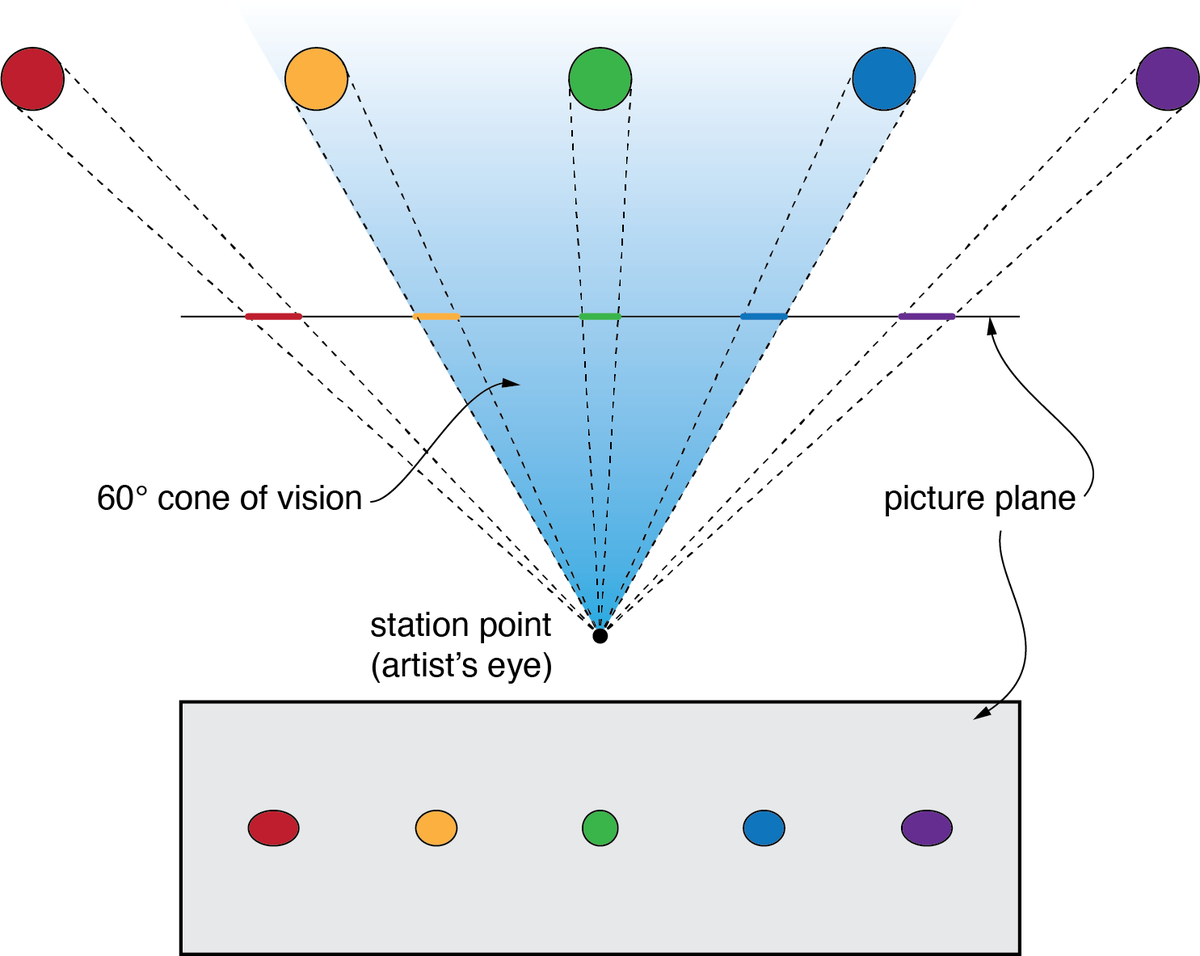
I drew this to illustrate why perspective artists choose to keep their artwork within a small (60° is common) "cone of vision." They often say it is to "avoid distortion." What do they mean? That's what this image is intended to convey. At the top I've presented the view 1/7 from above. The "picture plane" is the artist's canvas, the "station point" is the artist's eye, and on the other side of the canvas are five spheres of equal size that are hovering at the artist's eye level. One might think the spheres will appear as circles on the canvas, 2/7

On a whim, I decided to see if there was a 3D printable design of the 1962 game TwixT. Indeed there is! thingiverse.com/thing:118571 This is a 2-payer game my dad and a friend loved to play when I was a young kid. It is a very challenging game to play well! Like the game Hex, the 1/5 objective of TwixT is to make a path from one side of the board to the other (one player left-to-right, the other top-to-bottom). Players have pegs and bridges of their own color. Each turn the player can insert one peg into the 24x24 grid, and then they can place as many 2/5

I like this quote from Fields Medalist Steven Smale's 1998 article "Finding a Horseshoe on the Beaches of Rio." It illustrates that even the most accomplished mathematicians have an incorrect intuition and that learning math is hard, takes time, and can only be done by 1/7 by doing the math yourself. The context of the quote: Smale receive a letter from Levinson pointing out that an old example by Cartwright and Littlewood was a counterexample to one of his conjectures.

"I worked day and night to try to resolve the challenge to my beliefs 2/7

Today's rabbit hole: I've been reading about homotopy groups of spheres, the Hopf fibration, etc. Homotopy groups are a way of describing how spheres of one dimension can be mapped into spheres of other dimensions. The first homotopy group, the fundamental group, is easy to 1/7 calculate for all spheres, but computing higher homotopy groups is notoriously challenging. Here's a chart showing some of them. Note that those below the diagonal are zero because a sphere of lower dimension inside one of higher dimension can always be shrunken to a point. 2/7