
AI researcher with a focus on geometric DL and equivariant CNNs. PhD with Max Welling. Master's degree in physics.
How to get URL link on X (Twitter) App

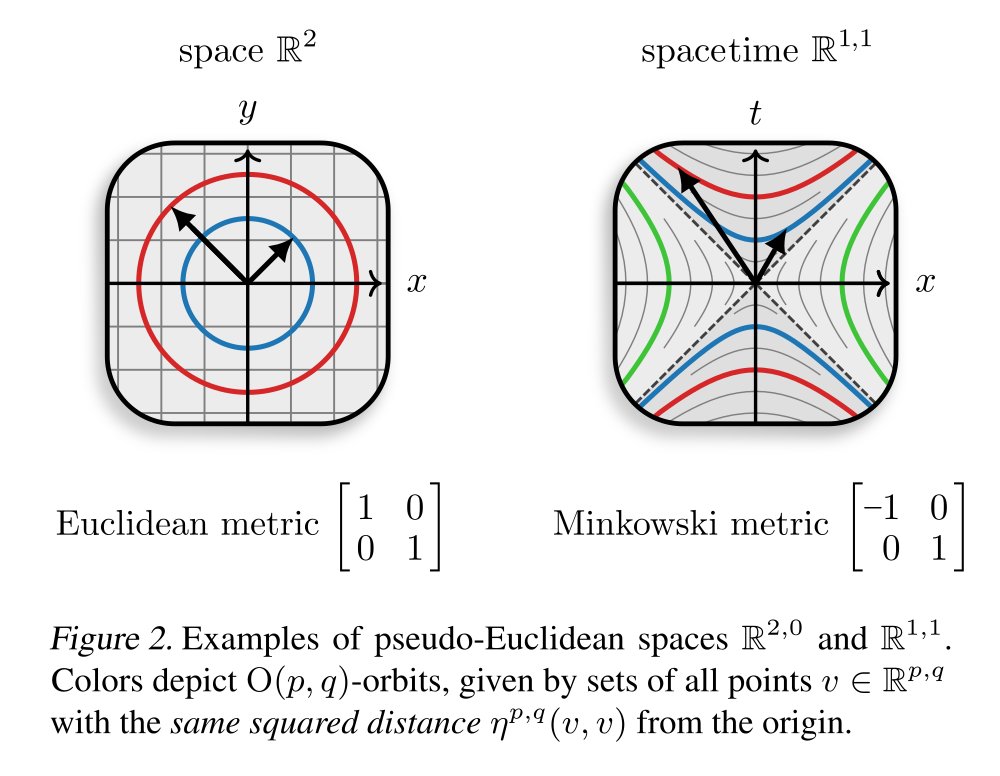

 Instead of restricting to one specific group, we allow for *any* affine groups Aff(G). They always include translations (ℝᵈ,+). In addition, they contain any choice of matrix (sub)group G≤GL(d), which allows to model rotations/reflections/dilations/shearing/...
Instead of restricting to one specific group, we allow for *any* affine groups Aff(G). They always include translations (ℝᵈ,+). In addition, they contain any choice of matrix (sub)group G≤GL(d), which allows to model rotations/reflections/dilations/shearing/...
 The book brings together our findings on the representation theory and differential geometry of equivariant CNNs that we have obtained in recent years. It generalizes previous results, presents novel insights and adds background knowledge/intuition/visualizations/examples.
The book brings together our findings on the representation theory and differential geometry of equivariant CNNs that we have obtained in recent years. It generalizes previous results, presents novel insights and adds background knowledge/intuition/visualizations/examples.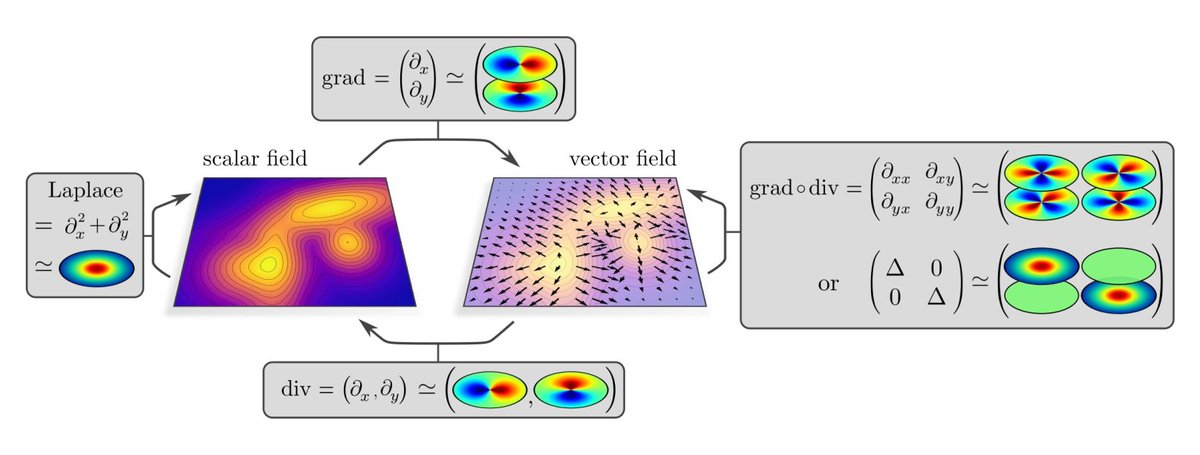
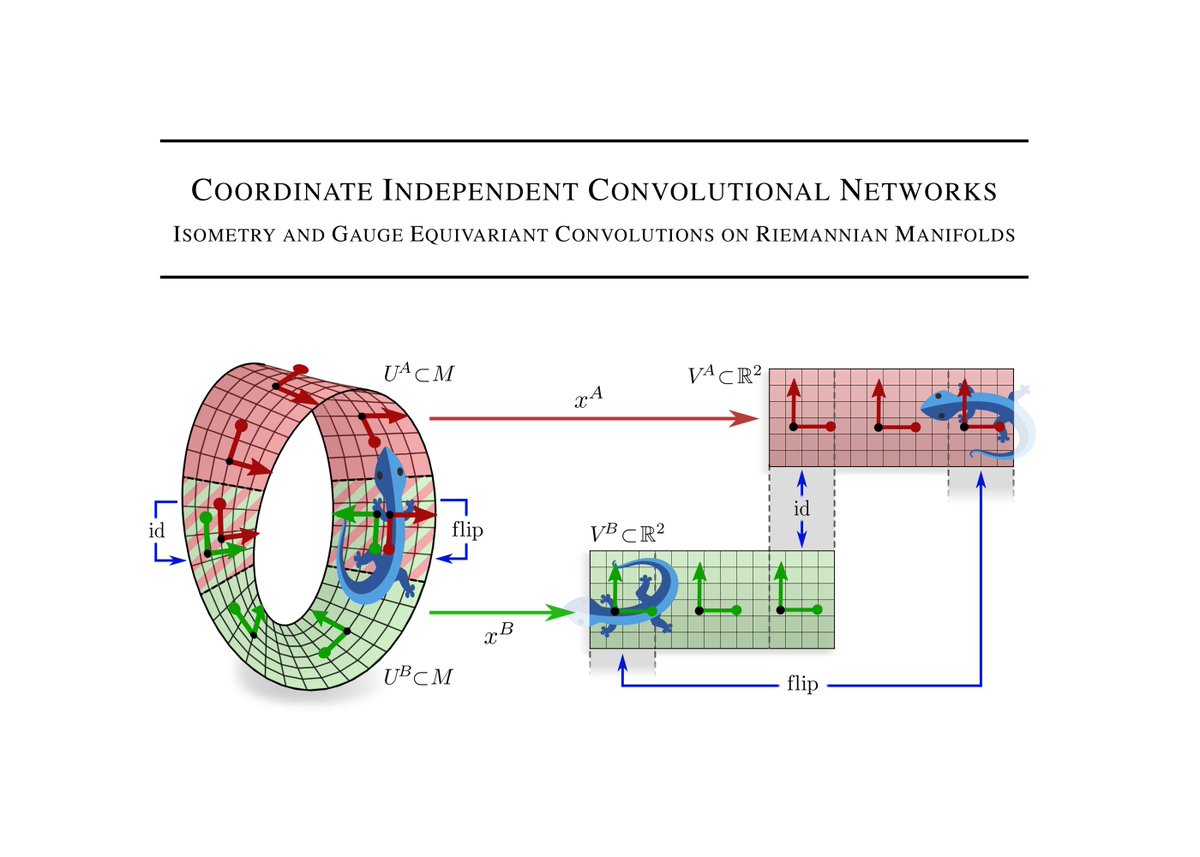
 Why *coordinate independent* networks? In contrast to Euclidean spaces R^d, general manifolds do not come with a canonical choice of reference frames. This implies in particular that the alignment of a shared convolution kernel is inherently ambiguous.
Why *coordinate independent* networks? In contrast to Euclidean spaces R^d, general manifolds do not come with a canonical choice of reference frames. This implies in particular that the alignment of a shared convolution kernel is inherently ambiguous.
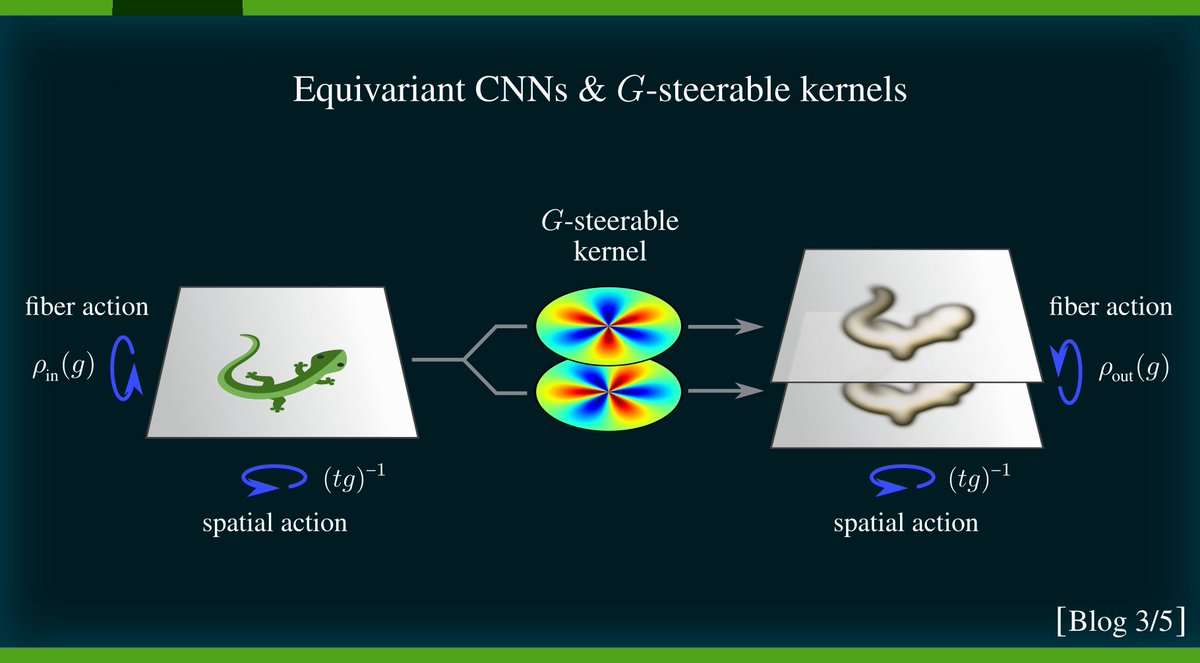
 Recent work by @TacoCohen and @wellingmax proved that *any* equivariant convolution requires G-steerable kernels, satisfying a linear constraint depending on the features' group representations rho_in and rho_out.
Recent work by @TacoCohen and @wellingmax proved that *any* equivariant convolution requires G-steerable kernels, satisfying a linear constraint depending on the features' group representations rho_in and rho_out.