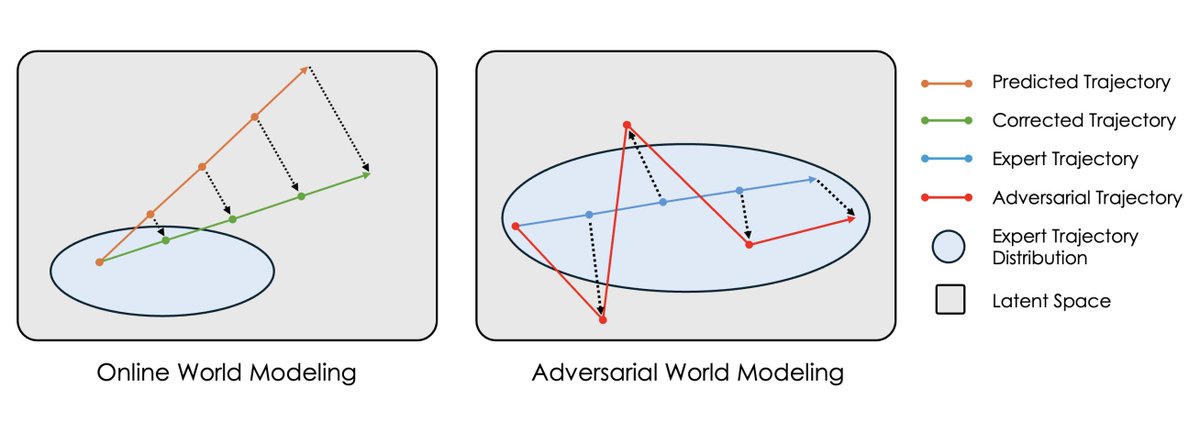
For a long time, Yann LeCun and others believed in gradient-based planning, but it didn’t work very well … until now. Here’s how we did it using incredibly simple techniques. But first, an introduction to gradient-based planning: 🧵1/11 Gradient-based planning starts with a world model that takes in the current state (e.g. an image) and an action, and predicts the next state. We can stack this world model on top of itself again and again, turning it into a differentiable simulator of the environment. 2/11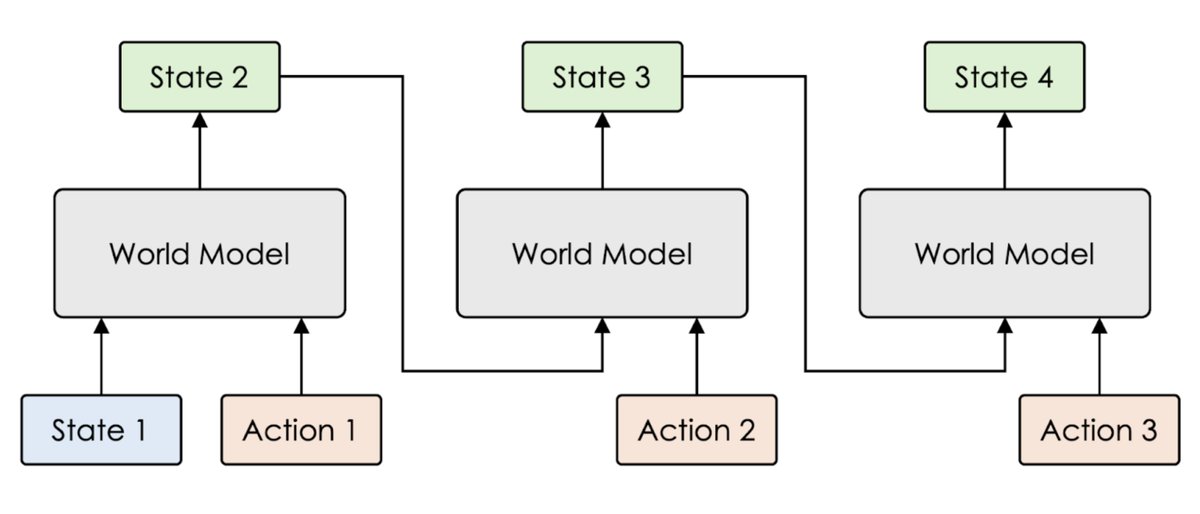

🚨 Did you know that small-batch vanilla SGD without momentum (i.e. the first optimizer you learn about in intro ML) is virtually as fast as AdamW for LLM pretraining on a per-FLOP basis? 📜 1/n Here's ★how to make small batch LLM training fast, ★how to pretrain LLMs efficiently via vanilla SGD without momentum, and ★why you should consider getting rid of LoRA and gradient accumulation. 2/n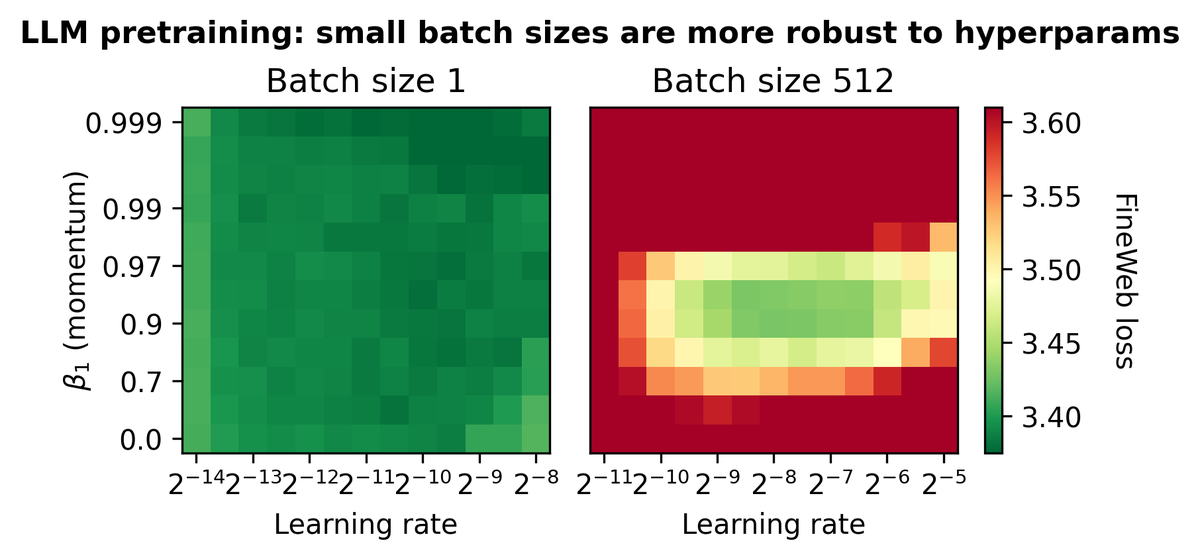

AI web agents like Operator and Anthropic’s Computer Use can operate a browser, but the LLMs inside are brittle, and you can’t trust what’s on the web. In this 🧵, I’ll show how adversaries can fool Anthropic’s web agent into sending phishing emails or revealing credit card info. We can sneak posts onto Reddit that redirect Anthropic’s web agent to reveal credit card information or send an authenticated phishing email to the user’s mom. We also manipulate the Chemcrow agent to give chemical synthesis instructions for nerve gas.

Do LLMs simply memorize and parrot their pretraining data or do they learn patterns that generalize? Let’s put this to the test! We compute the first generalization guarantees for LLMs.

w/ @LotfiSanae, @m_finzi, @KuangYilun, @timrudner, @andrewgwils



1/9arxiv.org/abs/2312.17173 LLMs are big, so they can memorize tons of training data, even randomly generated text where generalization is impossible. How do we tell generalization from memorization, especially in models trained on so much data that we don’t know what test samples they haven’t seen yet? 2/9

🚨Here’s an intuitive explanation for why training on lots and lots of data creates emergent properties, for instance math and reasoning, in large language models like #GPT-4 and #ChatGPT 🚨 1/17 Let’s start with the basics. Real-world data is full of patterns and structure. This structure allows us to describe things with simple rules. We exploit this fact all the time, for example to derive laws of physics or differential equations. 2/17

The following statement, while a commonly held view, is actually false! “Learning theory says that the more functions your model can represent, the more samples it needs to learn anything”. 1/8

https://twitter.com/ylecun/status/1591463668612730880

While it is true that a model which can only express few functions needs few samples to learn, the converse is not true! This underscores the failure of ideas like VC dimension and Rademacher complexity to explain neural network generalization. 2/8

How much data are augmentations worth? We show that augmentations can actually be worth more than extra data and invariance! They increase variance across batches, and this extra stochasticity finds flatter minima. arxiv.org/abs/2210.06441 1/8 As we gather more and more data, if we train without augmentations, we expect to saturate the performance of our model. This is not true under data augmentations! If augmentations are inconsistent with the data distribution, we will never overcome them. 2/8