Thread by @ClaraGrima

Tal día como hoy, 2 de septiembre, en 1865, con 60 años de edad y tras un fuerte ataque de gota, moría, en Dublín, William Rowan Hamilton, uno de los mejores matemáticos de Irlanda, por supuesto, y del mundo en general.

Fue y es un matemático muy querido por los físicos (al menos, eso espero) porque fue Hamilton quien definió los cuaterniones (una generalización de los números complejos) y por aquello del operador hamiltoniano que usan tanto en mecánica cuántica o clásica.

Pero yo voy a aprovechar para hablar de Hamilton y los grafos. What else? ;-)

Un grafo es un objeto matemático formado por dos conjuntos. Un primer conjunto de vértices o nodos (que representamos con puntitos) y un segundo conjunto de aristas (que unen a algunos de estos puntitos por parejas).

Podéis pensar en Facebook, por ejemplo. Los usuarios serían vértices y unimos con aristas aquellos vértices que sean amigos en esta red social.

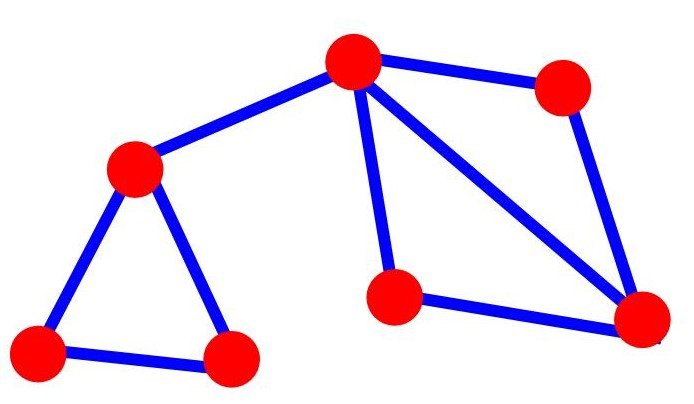
Pues bien, se dice que un grafo es un GRAFO HAMILTONIANO si podemos encontrar un recorrido cíclico (o ciclo) en él que pase por todos los vértices una (y solo una) vez volviendo al vértice del principio. Como el ciclo en azul que hemos pintado aquí:

No fue Hamilton quien planteó el problema ni tampoco el que dio la solución para saber cuándo un grafo era o no hamiltoniano. De hecho, no existe ningún teorema que nos dé una caracterización de grafo hamiltoniano.

Ah, se siente.

Hay algunas condiciones que son necesarias. Por ejemplo, que no haya vértices con una sola arista (con un solo amigo) porque en ese caso sería imposible cerrar el recorrido sin pasar dos veces por él, claro.

Pero la anterior no es una condición suficiente para que el grafo sea hamiltoniano. El de la siguiente figura no tiene ningún vértice con una sola arista y es imposible encontrar un ciclo hamiltoniano.

Posiblemente, el problema de encontrar este tipo de ciclos (o recorridos) en un grafo se remontan a muchos siglos antes de que naciera Hamilton y se lo plantearon no matemáticos sino jugadores de ajedrez.

En el siglo IX, por ejemplo, Al-Adli Al-Roumi, un jugador de ajedrez árabe, autor del primer libro sobre ajedrez (creo), ya hablaba del problema del caballo.

El problema del caballo consiste en, en un tablero de ajedrez, empezar con un caballo en una posición cualquiera y, usando los movimientos de caballo, pasar por todas las casillas del tablero una y solo una vez.

Aquí tenéis una solución con un camino abierto (no empieza y termina en la misma casilla) pero es monísima :)

Muchos matemáticos intentaron resolver el problema del caballo con ciclo cerrado, incluído el mismísimo Euler (paro aquí para hacer aquí una genuflexión) como la que viene en la figura.

Hay muchísimas soluciones diferentes. De hecho, no se sabe cuántas. ¿Quieres intentar la tuya? ;-)

Os estaréis preguntando, ¿por qué razón se llaman grafos hamiltonianos a los grafos que tienen un recorrido cíclico que pase por todos los vértices una y solo una vez? Pues porque fue Hamilton el que inventó en 1856 el juego Icosian.

El juego Icosian consiste en encontrar un recorrido cíclico hamiltoniano en las aristas de un dodecaedro (visitando una y sólo una vez cada vértice y que el vértice de llegada coincida con el de partida).

Puede que a alguien este rompecabezas le recuerde a los famosos puentes de Königsberg (problema que se considera el origen de la Teoría de Grafos que fue resuelto por Euler (paro otra vez para hacer otra genuflexión)) que tan bien os expliqué aquí :P

pequenoldn.librodenotas.com/matiaventuras/…

Pero no es el mismo problema, ni se le parece. En el de los puentes de Königsberg se trata de pasar por todas las aristas (rayitas) del grafo una y solo una vez y en el problema de Hamilton se trata de pasar por los vértices una y solo una vez.

Digamos que el problema de Königsberg es el del camión de la limpieza, que tiene que pasar (o debería) por todas las calles y el de Hamilton es el del repartidor que tiene que llegar a todas las casas (puntitos) pero no tiene por qué recorrer todas las posibles calles.

De hecho, mientras que resolver el problema de Königsberg y saber si un grafo es euleriano es trivial el problema de saber si un grafo admite un recorrido hamiltoniano es endiabladamente complicado. Formalmente, decidir si un grafo es hamiltoniano es un problema NP-completo.

Aquí @twalmar os explica mejor que nadie esto de los problemas NP ;-)

Pero aunque sea un problema complicado de resolver en general, podéis intentar jugar con grafos pequeños y proponer a amigos (o enemigos) que encuentren en ellos un ciclo hamiltoniano (que pase una y solo una vez por cada vértice y que empiece y termine en el vértice).

Os dejo este para que lo intentéis :)

Vale, no os enfadéis. No tiene solución pero os servirá para una tarde de lluvia que no podáis ir al parque y el niño (o la niña) se ponga un poco nervioso (o nerviosa) :)

o puedes tener toda la tarde intentando hacer un caminito que empiece y termine en el mismo punto y que pase por cada puntito una y solo una vez ;-P

Por cierto, este grafo se llama grafo de Herschel.

También sirve para entretener a familiares o amigos molestos y/o presumidos.

Lo sé: me tenéis que querer 🙃

Y nada más por el momento. Seguid disfrutando de vuestras vidas todo lo que podáis :)

Os quiero ❤️

A casi todos.

Aquí está el hilo desenrollado por @threadreaderapp (gracias a @el_lector, no conocía esta app 🙂)

threadreaderapp.com/thread/1168491…