Thread by @insectsoup

Social distancing is a Public Good: the more people who do it, the more disease we avoid. I benefit from you isolating. You benefit from me isolating.

But it's clear we have a polymorphism: some people are Team #SelfishPricks, and some are Team #StayAtHome.

Why?

This is a game-theory problem, and since I am indeed #StayingAtHome, why not spend some time exploring a game-theoretical concept that predicts such a polymorphism: Non-Linear Public Goods?

We start with Hardin (1968. Science 162:1243–1248.), who published one of the most cited and influential papers of all time: The Tragedy of the Commons. Hardin’s Tragedy is also known as an N-person Prisoner’s Dilemma, aka NPD.

In the NPD, the more people who contribute, the more public good is produced, until the maximum amount of public good is produced when everybody contributes. Everyone who self-isolates reduces disease transmission, and if everybody isolates, transmission is stopped completely.

The problem is the #SelfishPricks. If everybody ELSE pays the cost of isolating, a cheater can go out while still benefiting from the public good (health). Since anyone can be the exception, we expect everyone eventually to join Team #SelfishPricks
bit.ly/2VnqNJv

Hardin’s answer to cheaters was “Mutual Coercion, mutually agreed upon,” which includes top-down enforcement (policing) and privatisation (back gardens). Elinor Ostrom, 2009 Nobel Laureate in Economics, later changed the focus to social norms (peer enforcement)

#SelfishPricks aren’t limited to humans. Here’s a great review by Daniel Rankin et al. (bit.ly/3b0WgYq) who describe biological Tragedies of the Common.

In biology, the NPD predicts that cheaters take over completely unless there are external, countervailing forces: kin selection or positive assortment (cooperators helping only cooperators). Biologists have found ways for non-thinking organisms to achieve positive assortment.

But here’s the thing: Hardin’s Tragedy (i.e. NPD) is NOT a good description of natural or societal public goods. The reason is simple: the NPD assumes that the public good accumulates linearly. Each cooperator’s contribution increases the public good by a fixed amount.

2 cooperators produce twice the public good that 1 cooperator does.

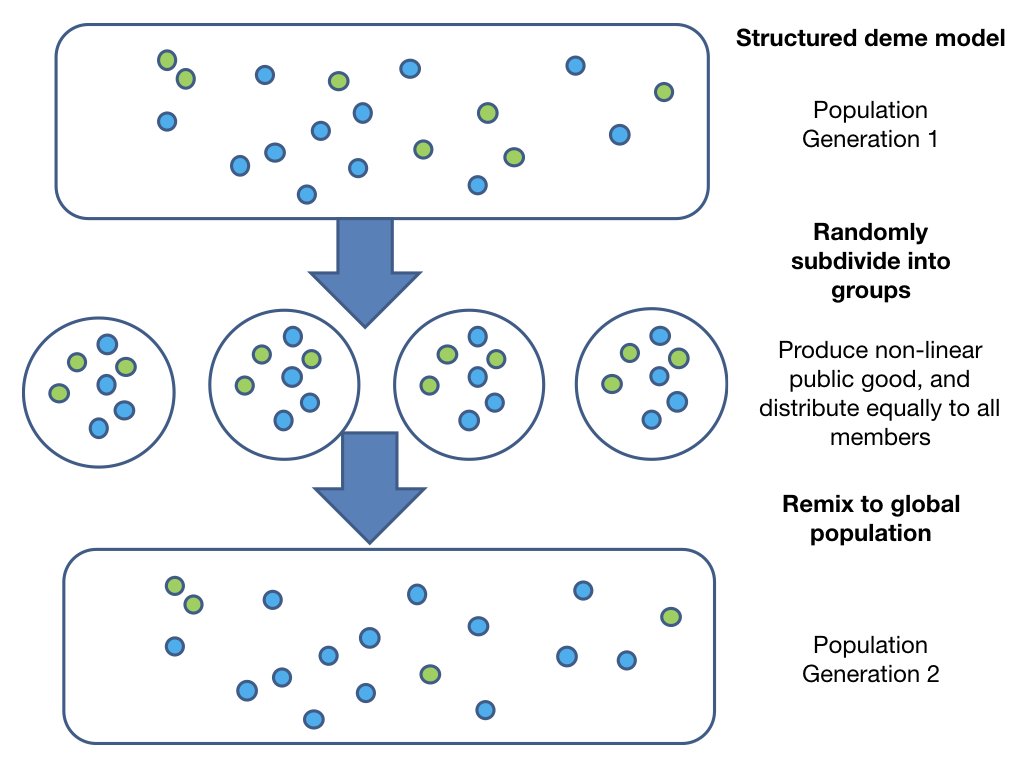
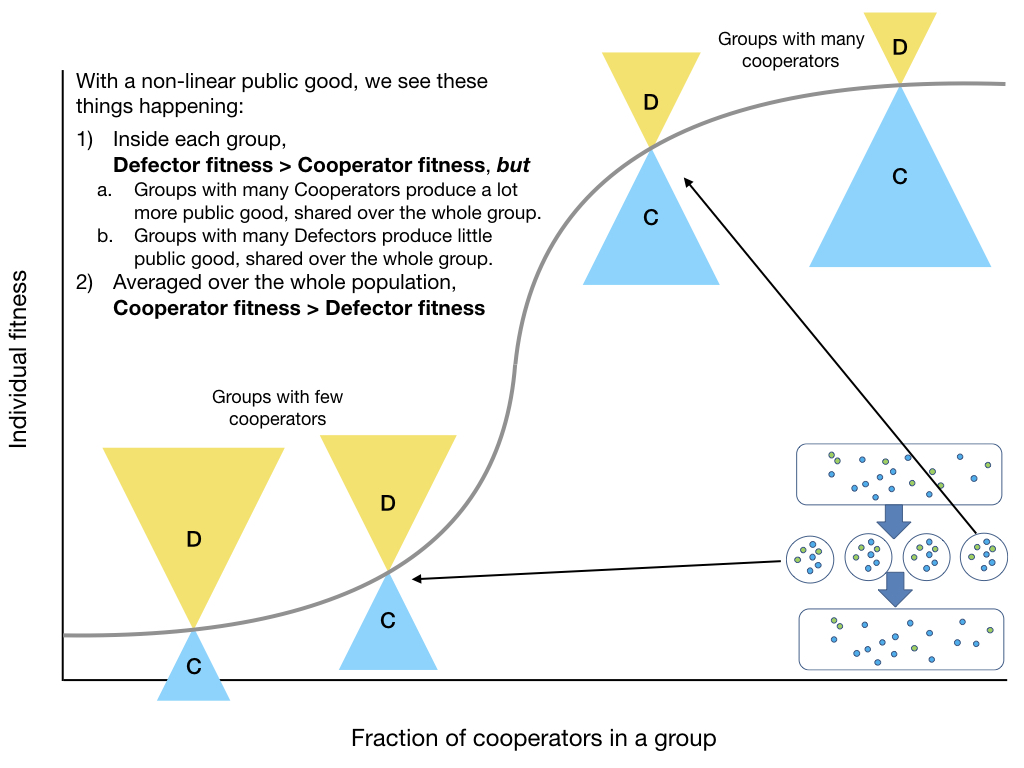
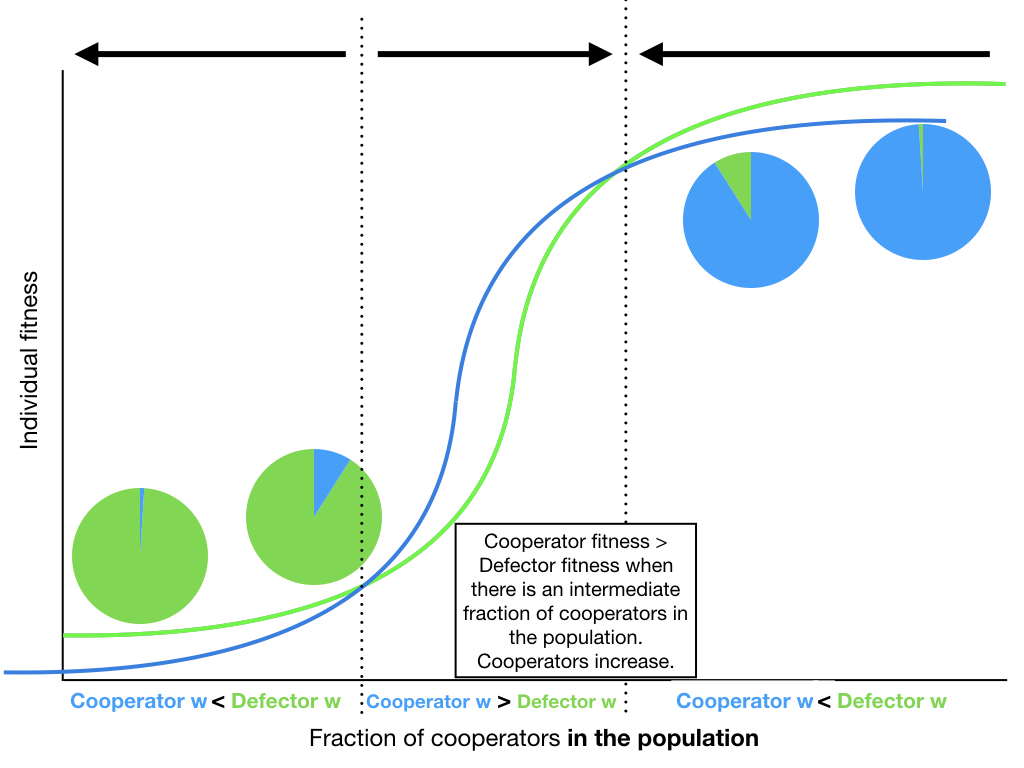
10 cooperators produce 10 times the public good that 1 cooperator does.

And so on.

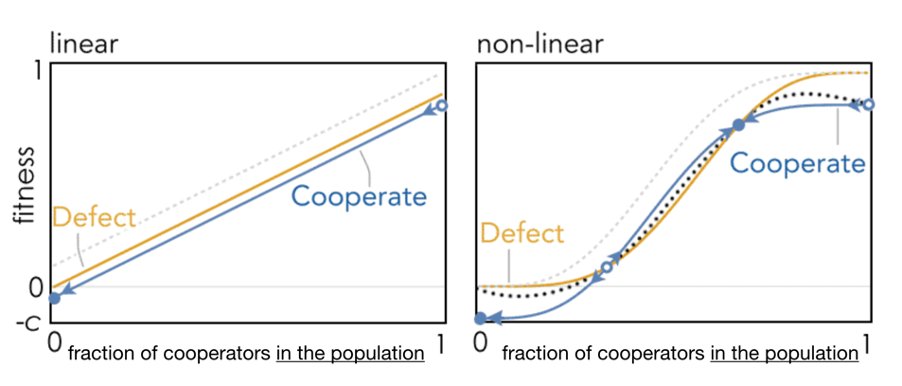
This seemingly innocuous assumption is not realistic.

As far as we know, not a single biological or societal public good is linear.

Here is a bunch of examples (stylised for graphical prettiness):

Real public goods are NON-linear.

Nonlinearities arise because the effect of biological molecules is sigmoidal, due to cooperative ligand binding. In social interactions, nonlinearities arise when just a portion of a group is large enough to detect a predator, take down a large prey, or reproduce successfully.

In human societies, herd immunity from vaccination is a threshold-effect public good (a very steep sigmoid curve). In climate change, there are critical greenhouse-gas concentrations below which the climate will avoid runaway feedback.

There are many possible curves; all have a region where a few additional cooperators sharply raises the amount of public good produced. With this added realism, cooperation can be stable in well-mixed, structured populations of unrelated individuals, including cheaters.

Here’s why: let’s start with a structured deme. A population is randomly divided into small groups, each with some cooperators who produce the public good, which is shared equally over the whole group, including cheaters. The groups with more cooperators produce more public good.

Cooperators, by definition, mainly find themselves in groups with other cooperators, thereby producing a lot of public good. Defectors mainly find themselves in groups that produce little public good. (Most of a type are found in groups dominated by that type, right?)

Averaged over all groups, cooperators have higher fitness, *even though* within each group, defectors have higher fitness! Chuang et al. pointed out that this has been called Simpson’s Paradox.

We can look at this dynamically. In any given group, cooperators have lower fitness than defectors do, because the cooperators, by definition, make a costly contribution to the public good. This shifts the cooperator fitness line down.

However, the amount of public good received by a defector depends on the number of cooperators in its group, while the amount received by a cooperator depends on the number of cooperators in its group *PLUS ITS OWN CONTRIBUTION*. This shifts the cooperator line to the left.

There is a now region where cooperator fitness > defector fitness. When cooperators are at intermediate pop. frequency, a final cooperator joining a group is likely to cause that group’s PG production to shoot up, which more than pays the cost of contribution.

There are 3 equilibrium pts. The rightmost one is the stable polymorphism: cooperators & defectors coexist. Defectors can invade when rare but do not drive cooperators to extinction. Stability is endogenous for non-linear public goods. No positive assortment or enforcement needed

Is there evidence for non-linearity and stable coexistence of cooperators and cheaters? YES! A key reported observation is that colony growth rates are maximal at intermediate cooperator frequencies, whereas the NPD predicts maximal growth rate only when cooperators are at 100%

Hardin’s Tragedy is LINEAR, which is easier to model but is an edge case and has no stable polymorphism. Non-linear public goods are the general case and in structured populations, have the possibility of a stable polymorphism, no positive assortment or enforcement needed

The best evidence so far for non-linear public goods and stable polymorphism is from microbes and tumors.

What about humans? Why do we have #SelfishPricks AND #StayAtHome? Let’s turn to the late, great Elinor Ostrom:

I’ll end with a hypothesis: humans evolved to play non-linear public-goods games. We should expect humans to display a mixture of cheater and cooperator personalities. Different institutional settings then favour one over the other. I see Ostrom’s design principles in this light.

I am very fortunate to have learned about non-linear public-goods games from Marco Archetti (bit.ly/2XsMLgw) and István Scheuring (bit.ly/2JVNleV) (neither on Twitter), who generalised work that began in the 1970s.

now out in preprint: Archetti et al. The Non-Tragedy of the Non-Linear Commons.

Trying to decide where to submit this:
preprints.org/manuscript/202…