Thread by @alexjc

Let's start our tour of research papers where #generative meets deep learning with this classic by Gatys, Ecker and Bethge from 2015.✨

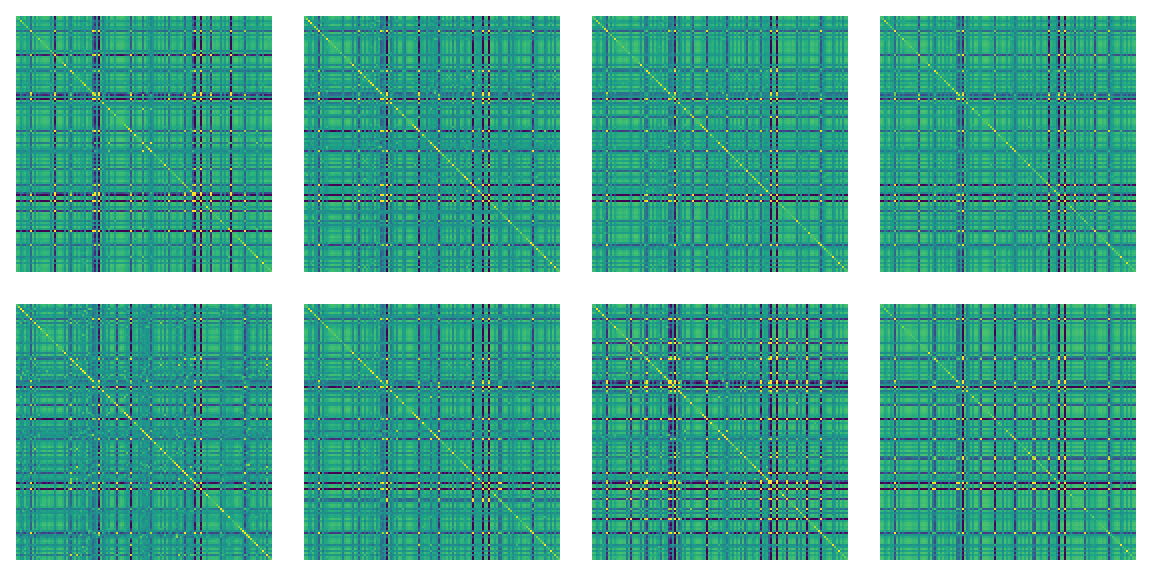
A multimedia tutorial & review in a thread! 👇

📝 Texture Synthesis Using Convolutional Neural Networks
🔗 arxiv.org/abs/1505.07376 #ai

Here's the nomenclature I'll be using.

✏️ Beginner-friendly insight or exercise.
🕳️ Related work that's relevant here!
📖 Open research topic of general interest.
💡 Insight or idea to experiment further...

See this thread for context and other reviews:

https://twitter.com/alexjc/status/1261235716295712768

The work by Gatys et al. is an implementation of a parametric texture model: you extract "parameters" (somehow) from an image, and those parameters describe the image — ideally such that you can reproduce its texture.

I'll be using these textures (photos) as examples throughout:

Once you have your parametric texture model, you can take any starting image (e.g. random noise) and optimize it so that the parameters match with the texture you want to reproduce.

This can take 50-100-500-1000 steps... At the beginning, the random images would look like this:

The optimization is done by gradient descent, the same technique behind deep learning, except it's the image that's being "trained" in this case.

📺Here are 500 steps of the optimization for the textures above:

So what are the "parameters" of a texture?

🕳️ Previous work by Portilla and Simoncelli used manually crafted feature detectors based on the visual cortex.

📝A Parametric Texture Model Based on Joint Statistics of Complex Wavelet Coefficients
🔗cns.nyu.edu/pub/lcv/portil…

The work by Gatys et al. instead uses a pre-trained convolution network. It also extracts features from an image, but it's based on a dataset of 1M real-world images instead of assumptions from neuroscience.😜

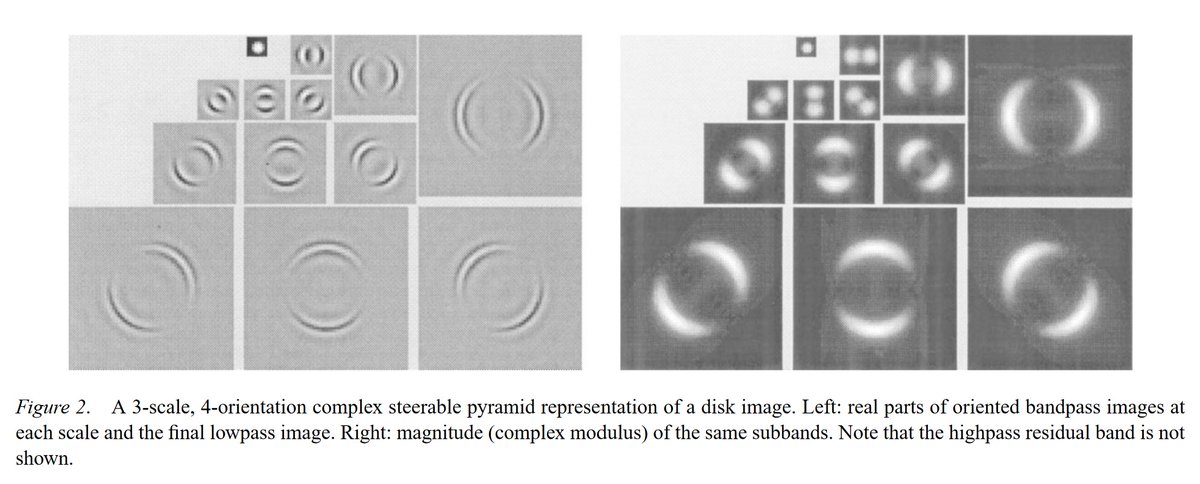
Here's what those features look like. (cw: 2fps strobe)

These are called "feature maps" and include information such as:
- colors detectors
- edges detectors
- pattern detectors

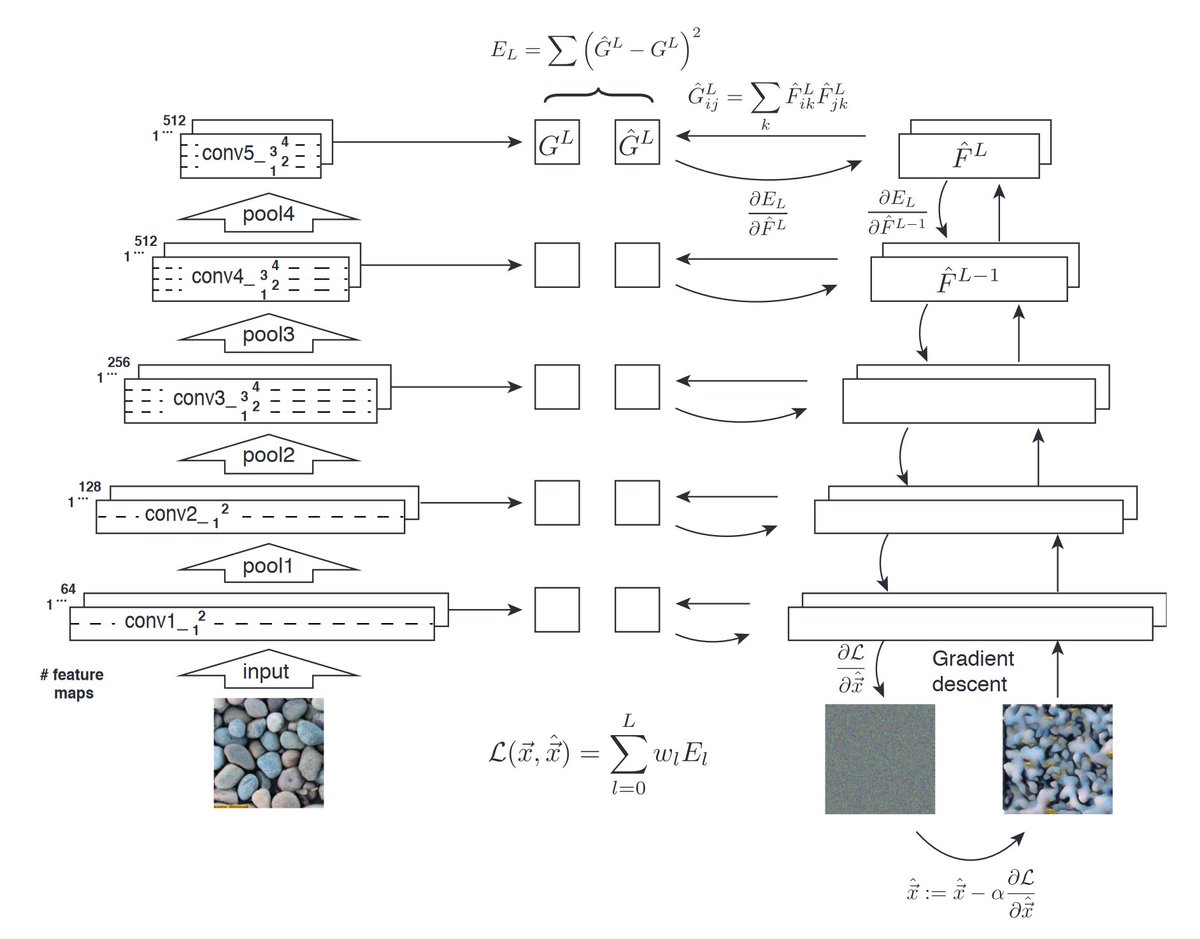
Then, the convolution network (convnet) extracts even more feature detectors from those low-level features. The next level looks like this:

These detectors were learned by training a convolution network on an image classification problem. So instead of hand-crafting a hierarchy of features for textures, deep learning helps compute those based on statistics from images.

The feature map at each level is 2x2 smaller:

At each level of the hierarchy, there are 2x more feature maps as well, so it looks like this:

(level, features, size)
L1 → 64 @ 256x256
L2 → 128 @ 128x128
L3 → 256 @ 64x64
L4 → 512 @ 32x32

Here are 512 tiny feature maps at level 4 of the hierarchy:

✏️ A good exercise if you're getting started, use a deep learning framework to extract these feature maps, and visualize them. (A CPU is fast enough for this.)

PyTorch for example has pretrained networks (the VGG family) that are suitable:
pytorch.org/hub/pytorch_vi…

Warning: You'll spend most of your time installing Python libs and figuring out how to access data in 4D "tensors."

🛠️ I created a repository to make it easier to access these feature maps. If you're interested, I can share my own visualization scripts: github.com/photogeniq/ima…

Now we have feature maps, but it's a lot of data! Even compressed, that's 100x bigger than the original image.

You can use these feature maps to reproduce the original image, but it's not a good texture model because it's "over parameterized" — i.e. it has too many constraints.

Gatys et al. combine all these feature maps into small "gram matrices" that express feature correlations. For example:

- vertical edges tend to be green
- horizontal edges tend to be blue

Here are examples of gram matrices for L1, they are like 2D histograms of 64 x 64:

The advantage of this "gram matrix" representation is that you discard positional information. When generating the image, you can figure out how it should be laid out in space while preserving the look & feel of the texture.

Here are the matrices for L2, they are 128 x 128:

These are like the fingerprints of a texture.

🙋 How do you read a gram matrix?

Each column represents a feature detector, and so does each row. Each item contains an estimate how often those features occur together for all pixels in the image.

(That's why it's symmetrical.)

Remember that we start the optimization from random noise? We can compute the gram matrices of those images too...

Here's what the fingerprint of greyscale noise looks like:

As you optimize the gram matrix of random noise to match the desired texture, here's how the fingerprint changes for each of the textures above:

📺 (I never visualized this before, it's pretty cool ;-)

Since there are gram matrices for each level of the feature hierarchy, you can decide which ones to use. This way, the new textures you generate capture patterns at different scales / octaves.

For example, here the textures are optimized with L1 only, and then L1-L5:

Since the error for each of the gram matrices (L1 ... L5) are minimized at the same time, the layers reluctantly cooperate to decide on the patterns in the final output.

✏️ Try an open-source implementation and tune the weights for each layer!

Disclaimer: I tried to represent the paper as accurately as possible in the visualizations. However my code may have accidentally included improvements discovered after the paper was published.

In particular, the original algorithm is infamous for producing desaturated patches:

To summarize:

1. Initialize with any image, e.g. random noise.
2. Iterate:
- Process it through a convnet to extract features.
- Extract the gram matrices from those features.
- Calculate the difference to the target gram matrix.
- Back-propagate gradients and update the image.

📖 There are many subtleties at each step:
- What are suitable convnets?
- How best compute the gram matrix?
- Which optimizer works fastest?

But this thread is already pretty long so I'll keep those discussions for reviews of downstream papers!

I uploaded my script that visualizes gram matrices here, along with a collection of normalized convolution networks that are suitable for this: github.com/photogeniq/ima…