Thread by @bslagter

Draadje over coronavirus, superverspreiding en de scheefheid van besmettingen. En dat je daaruit nog niet teveel conclusies kunt trekken (k is de nieuwe R). 👇

2/ De laatste dagen is er veel aandacht voor de ongelijke verdeling van besmettingen. Een goed artikel in de Volkskrant:

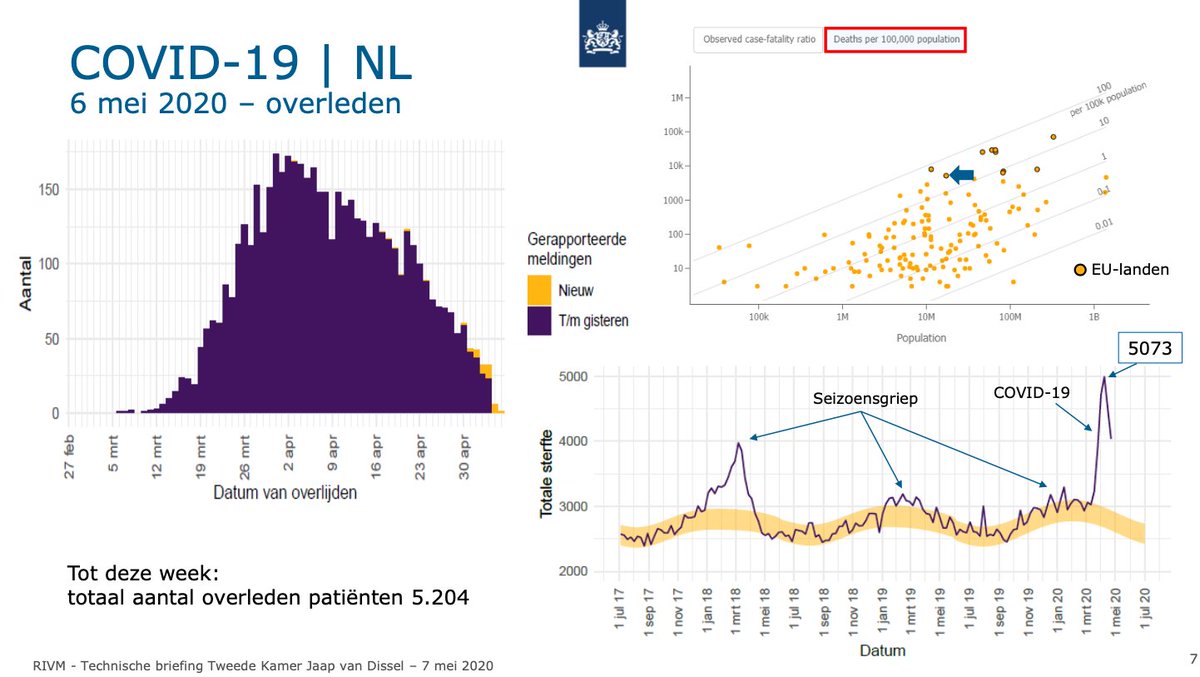
"Het virus zou eerder voldoen aan een 10/80-regel: 10 procent van de geïnfecteerden veroorzaakt 80 procent van de nieuwe gevallen"

volkskrant.nl/wetenschap/zin…

3/ De kern is dat reproductiegetal R een gemiddelde is van:

- veel mensen die heel weinig besmetten
- een paar mensen die heel veel besmetten

Begin april schreef ik daar een draadje over.

https://twitter.com/bslagter/status/1247117674544578563

4/ Hoe die besmettingen verdeeld zijn, wordt beschreven door dispersie-parameter k.

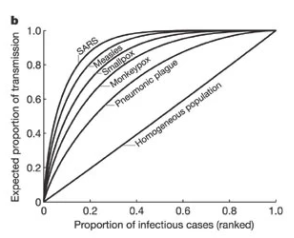
Als verspreiding homogeen is, dan zou iedereen exact R mensen besmetten. Dat gebeurt als k → ∞. Hoe lager de k wordt, hoe groter de variatie.

nature.com/articles/natur…

5/ In deze thread beschrijft @AdamJKucharski hoe dit werkt. Hij laat zien hoe besmettingen verdeeld zijn bij k=1000 en k=0,2. Groot verschil!

https://twitter.com/AdamJKucharski/status/1267737631481364480

6/ Om het begrijpelijk te maken heeft Kucharski deze tabel gemaakt. Bij k=0.1 wordt 80% van de besmettingen veroorzaakt door maar 9% van de mensen.

Verschillende studies komen voor het coronavirus op een k van tussen 0.1 en 0.5. Een enkele nog lager.

7/ Een heel lage k suggereert dat superverspreiding een groot aandeel levert in de totale verspreiding.

Begrijpelijk dus dat er de laatste tijd veel aandacht is voor mogelijke condities voor superverspreiding. Denk aan aerosolen, binnen/buiten, luchtvochtigheid, tijdsduur.

8/ De gedachte is dat als je superverspreiding voorkomt, dat het virus uitdooft. Neem de situatie met k=0.1. Als je de 9% weet op te sporen die voor 80% van de verspreiding zorgt, dan is daarmee R < 1.

Zie artikel in NYT: "Just Stop the Superspreading"

nytimes.com/2020/06/02/opi…

9/ Nu lijkt mij superverspreiding voorkomen een uitstekend idee.

Maar het lijkt me te kort door de bocht om te stellen dat we precies weten hoe dat moet, en dat we (dus) vast alle andere maatregelen overboord kunnen kieperen.

10/ Een virusverspreiding is een complex systeem. Daardoor zijn gevolgen van veranderingen (in omgeving, maatregelen, gedrag) moeilijk voorspelbaar, bijvoorbeeld door feedbacklussen en niet-lineaire verbanden.

11/ Zo is dispersie-parameter k is (net als R) geen eigenschap van het virus alleen, maar ook afhankelijk van het netwerk waarin het zich verspreidt. Denk aan omgeving, maatregelen, immuniteit, gedrag. Als daarin iets verandert, kan ook de k anders worden.

12/ Twee voorbeelden:

- Als er grote variatie is in gedrag van mensen (bijv. voorzichtigheid), dan zal k lager worden (meer variatie in R)

- Als superverspreiding wordt voorkomen (bijv. geen evenementen), dan zal k hoger worden.

13/ Zo zou het kunnen dat de studies die een heel lage k vonden zijn gedaan in omstandigheden waarbij mensen veel afstand hielden, door maatregelen of cultuur.

Geen representatieve omstandigheden voor "laat alle maatregelen maar los"

14/ Ik vind het daarom voorbarig om absolute en radicale conclusies te trekken op basis van superverspreiding en k.

We weten nog ontzettend veel niet over het virus, de verspreiding, de besmettelijkheid en dispersie-parameter k.

15/ Blijft wel staan dat de lage k interessant is. Met bron- en contactonderzoek kunnen clusters worden gevonden, en kunnen we steeds meer leren over hoe een besmettingen elkaar hebben opgevolgd.

https://twitter.com/pesla/status/1263014084485750785

16/ Voor ons liggen de zomermaanden, waarin we veel buiten zijn, makkelijker kunnen ventileren, vakantie nemen, en misschien lucht en licht ons helpen.

Hopelijk kunnen we die tijd gebruiken om zoveel te leren dat we in de herfst slimmer het 'griepseizoen' in kunnen!