¿Cómo modelarlo para tener un pronóstico total de muertes?
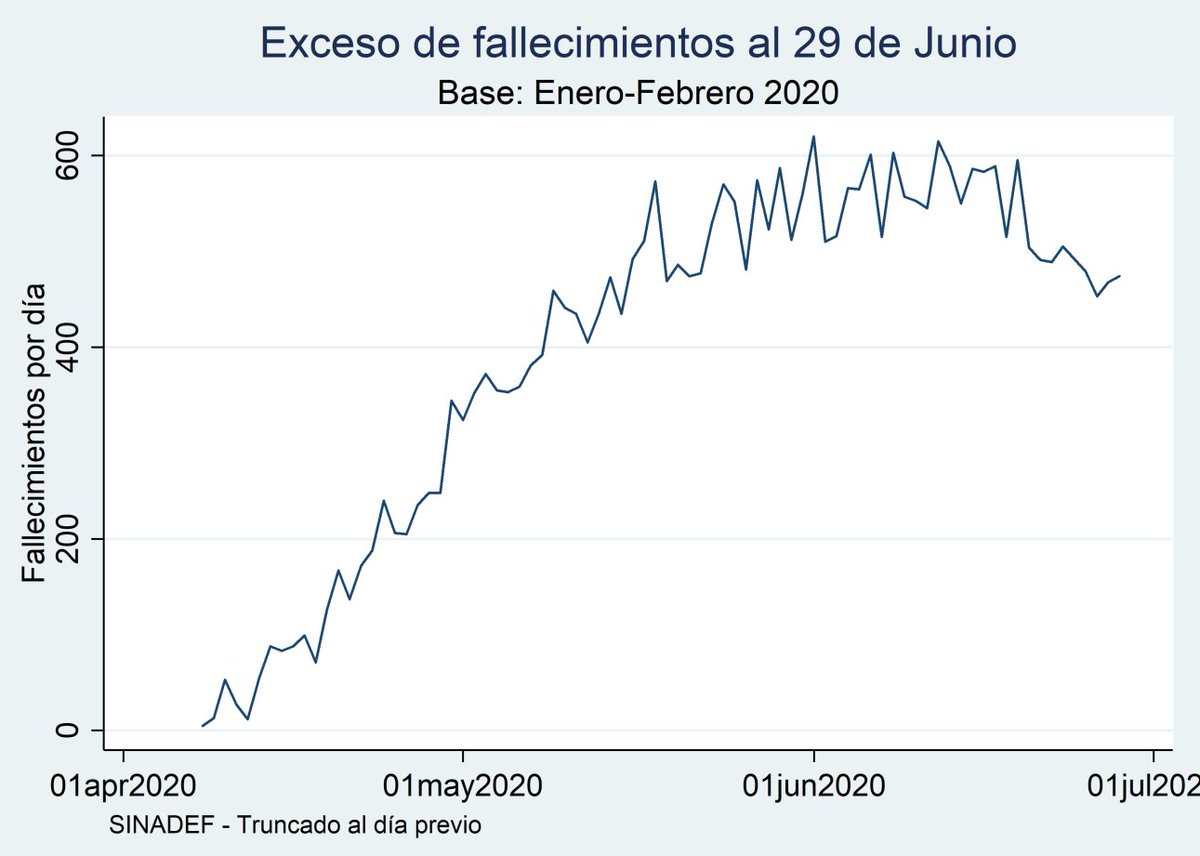
Si alguien ha intentado modelar la trayectoria de fallecimientos, quisiera conocer el método.
Comentarios en general son bienvenidos.

Keep Current with Farid Matuk
This Thread may be Removed Anytime!
Twitter may remove this content at anytime, convert it as a PDF, save and print for later use!

1) Follow Thread Reader App on Twitter so you can easily mention us!
2) Go to a Twitter thread (series of Tweets by the same owner) and mention us with a keyword "unroll"
@threadreaderapp unroll
You can practice here first or read more on our help page!