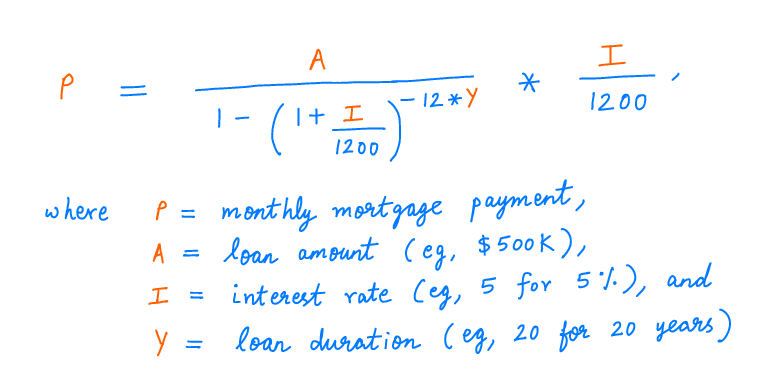Get a cup of coffee.
In this thread, I'll help you understand the calculations that go into mortgages.
This can help you take intelligent financial decisions -- how big a mortgage to take out, whether to pay it off early, etc.
When you take out a mortgage, the key question is: how much will your monthly payment be?
This depends on 3 factors: the size of the loan, the duration of the loan, and the interest rate you're able to get.
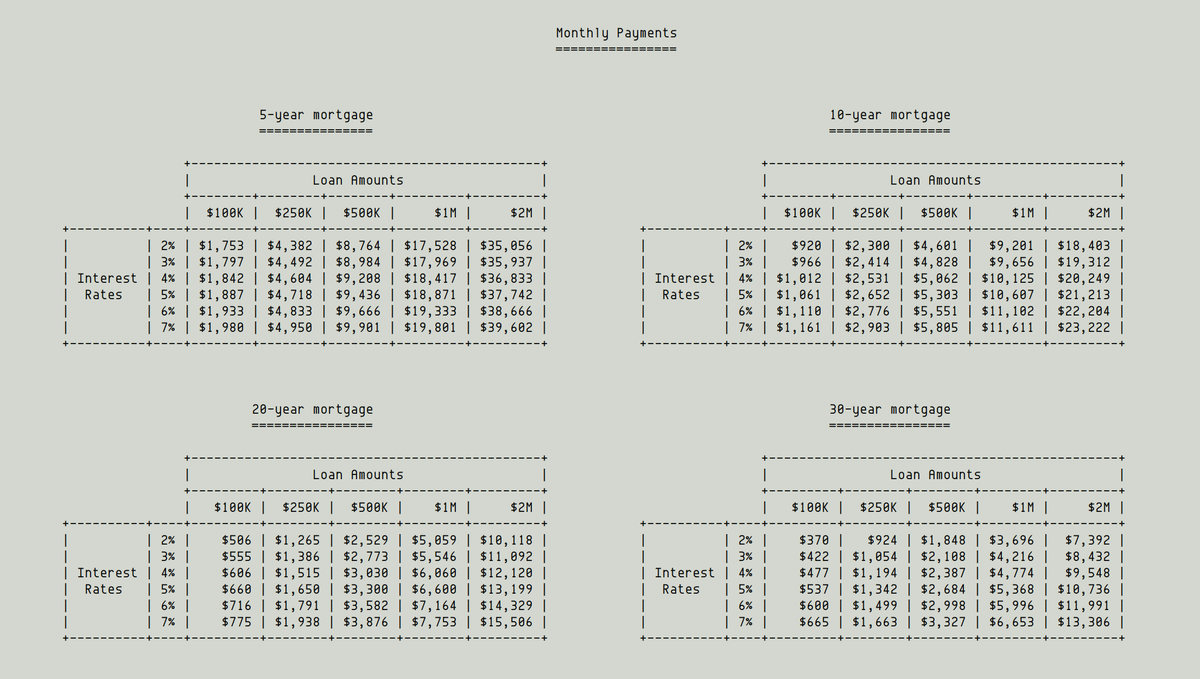
Size of the loan.
The more you borrow, the bigger your monthly payment.
For example, if you borrow $250K for 10 years at 4%, your monthly payment will be about $2,531.
But if you borrow $500K, your monthly payment will be $5,062.
Duration of the loan.
The longer you take to pay off the loan, the smaller your monthly payment.
For example, a $500K mortgage at 3% means $4,828 per month if you pay it off over 10 years.
But if you pay it off over 20 years, you only pay $2,773 per month.
Interest rate.
The higher your interest rate, the bigger your monthly payment.
For example, a 30-year $1M mortgage at 3% interest means $4,216 per month.
But at 4% interest, it's $4,774 per month.
Let's say you find a house you like.
And you're able to buy it -- by taking out a 20-year, $500K mortgage financed at 4% interest.
Congrats! You're now a home owner.
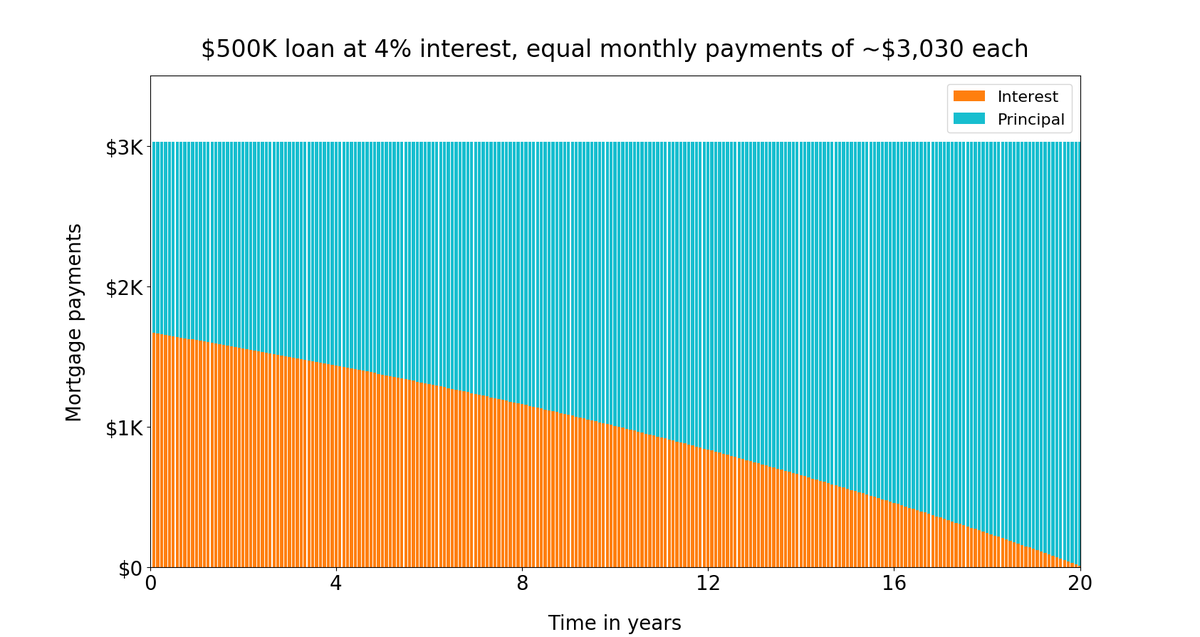
Your monthly payment works out to about $3,030.
It's useful to look at your mortgage through a couple different lenses.
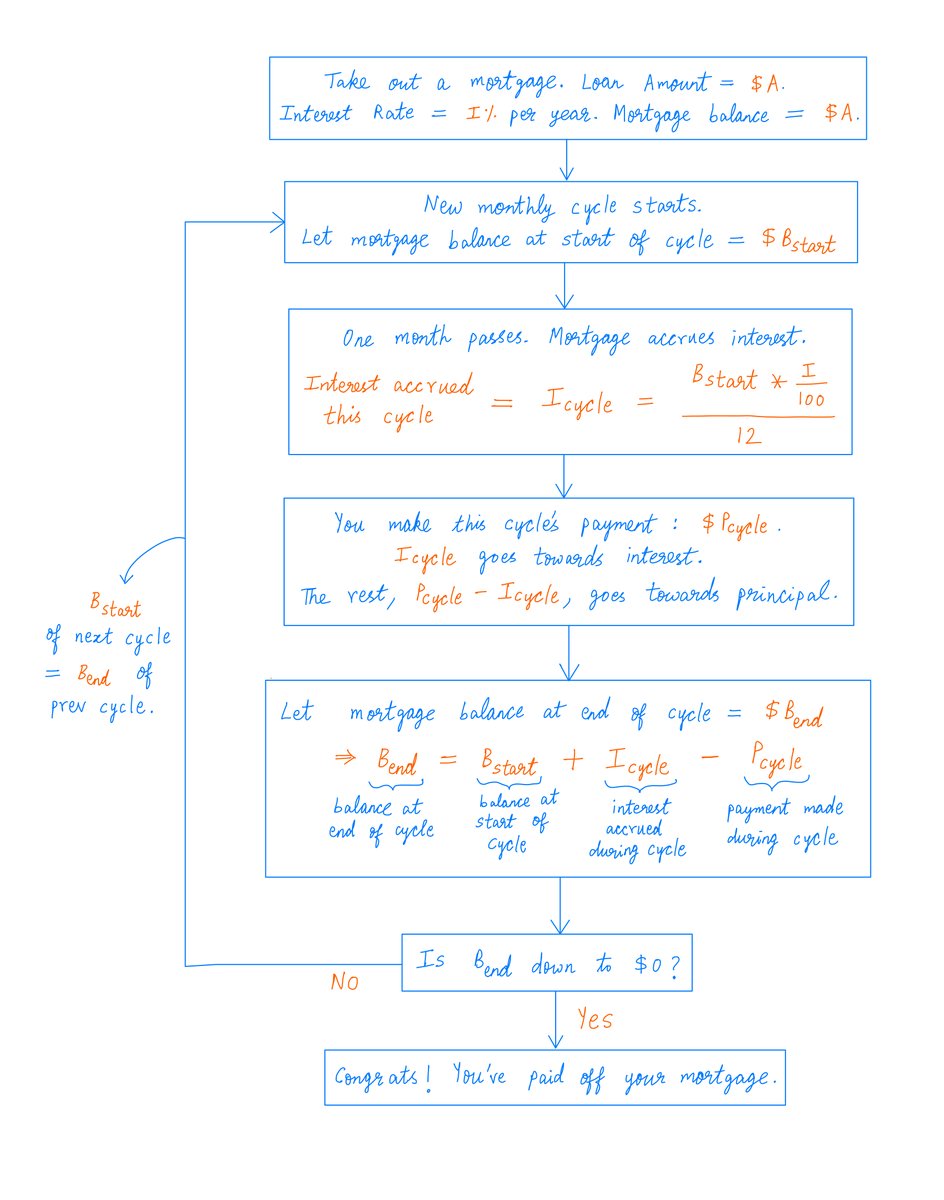
Lens 1: how much money do you owe the bank at any given time?
Lens 2: what portion of each monthly payment goes towards "principal", and what portion goes towards "interest"?
Let's apply this flowchart to your $500K mortgage.
At the beginning -- immediately after you take out the mortgage -- you owe the bank $500K.
In the first monthly cycle, the interest charged on this $500K will be $500K * (4/100) / 12 = $1,666.67.
So, when you make your first $3,029.90 payment, $1,666.67 of that payment will be used to pay interest, leaving $1,363.23 for principal. That's 55% interest, 45% principal.
At the end of the first cycle, you will owe the bank $500K + $1,666.67 - $3,029.90 = $498,636.77.
Here's the crucial thing: in the *second* monthly cycle, you'll pay interest *only* on this $498,636.77. *Not* on the original $500K.
So the interest will be lower. It's calculated the same way:
$498,636.77 * (4/100) / 12 = $1,662.12.
This means, when you make your *second* $3,029.90 payment, a *smaller* portion of it ($1,662.12) goes towards interest and a *bigger* portion ($1,367.78) towards principal. That's 54.86% interest, 45.14% principal.
At the end of the second cycle, you'll owe the bank:
$498,636.77 + $1,662.12 - $3,029.90 = $497,268.99.
Thus, over time, as you keep making monthly payments, the amount you owe the bank keeps going down.
And because you pay interest only on what you owe, your interest charges keep going down as well.
Over time, this leaves bigger and bigger portions of your monthly payments to go towards principal rather than interest.
That's all there is to the math.
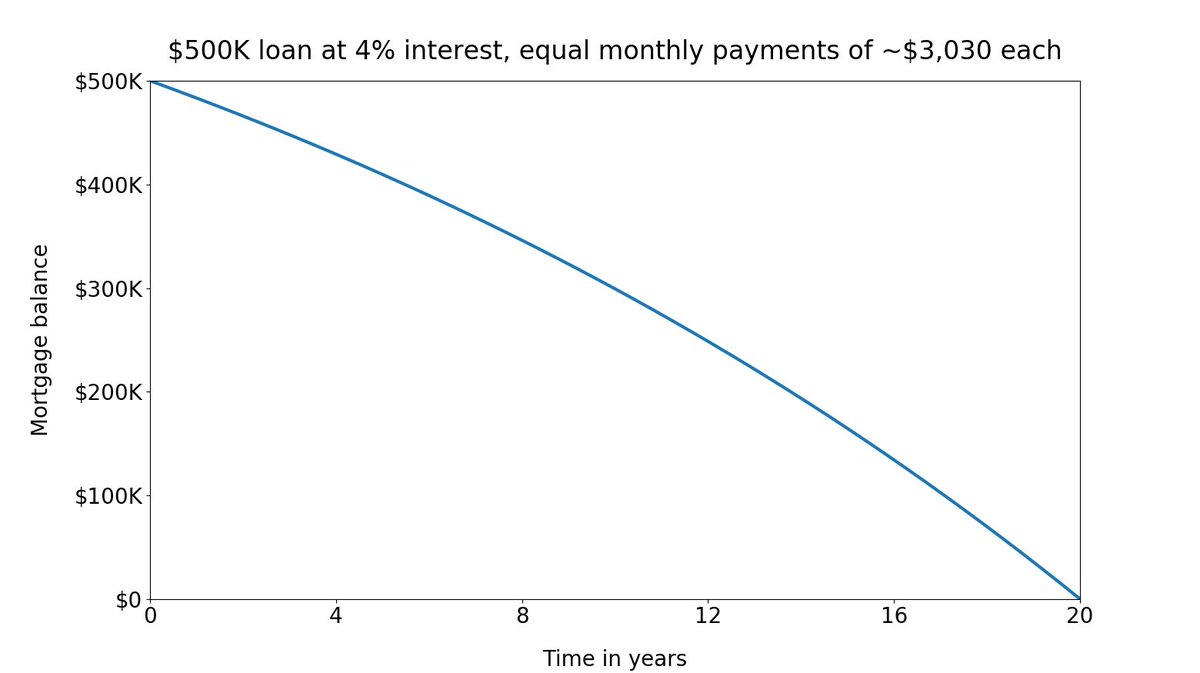
To be clear: each payment you make is ~$3,030. This is the total: interest + principal. This total doesn't change with time. See: the tops of the blue bars in the chart are flat.
What changes is how much of this total is interest and how much is principal.
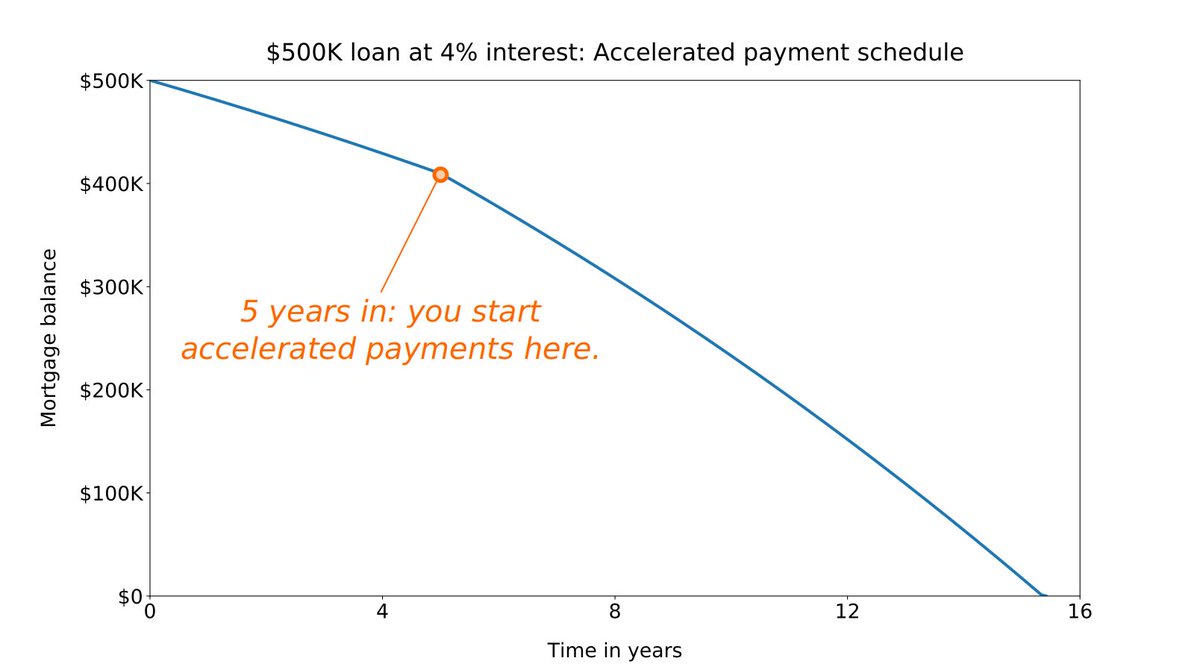
Fast forward 5 years into the mortgage.
You get a promotion at work. The promotion comes with a bigger salary.
Now that you're making more money, should you maybe pay off the mortgage early?
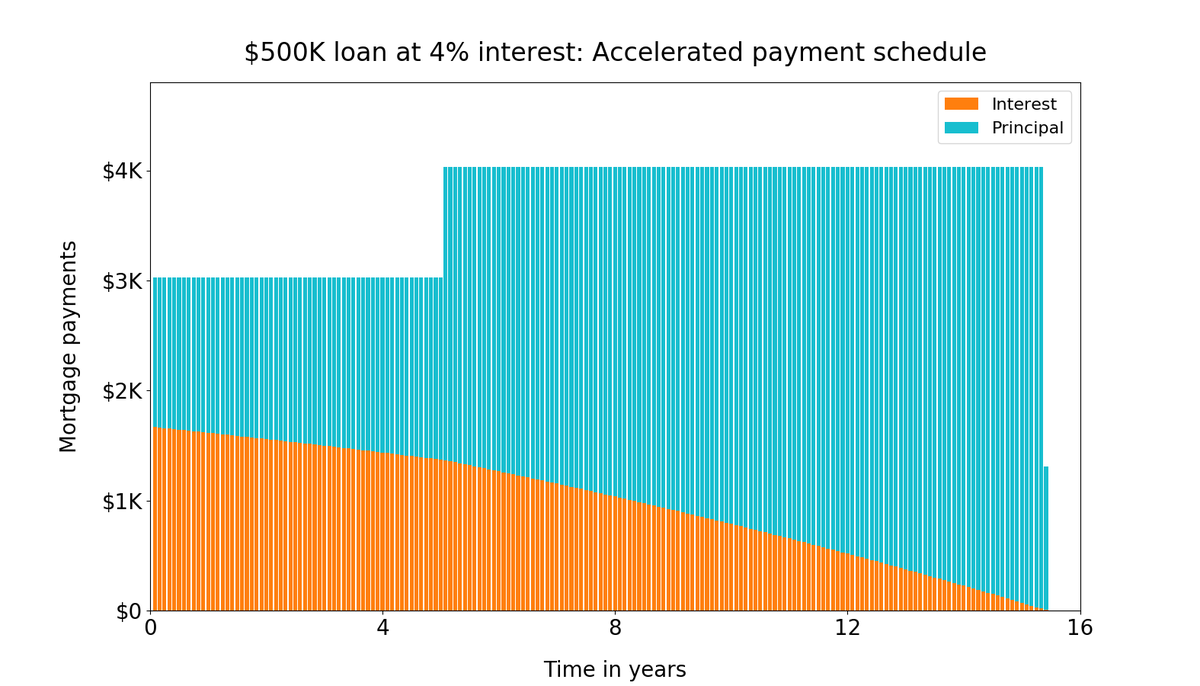
Suppose you step up your monthly payments by $1000. That is, instead of paying ~$3,030 per month, you start paying ~$4030 per month.
With this "accelerated" payment schedule, how soon will you have the mortgage paid off? And how much will you save on interest?
As the charts show, under the accelerated plan, you'll pay off the mortgage a full four and a half years ahead of schedule.
Plus, if you add up all your payments under the accelerated plan, the total is about $683K: $500K principal + $183K interest.
For the original plan, this is about $727K: $500K principal + $227K interest.
So the accelerated plan saves you about $44K in interest as well.
Key lesson: To understand the impact that a hypothetical change (e.g., an accelerated payment schedule, a refinancing, etc.) will have on your mortgage, simulate the changed plan "cycle by cycle" on the mortgage flowchart, and compare against the original plan.
One caveat: using excess cash to pay off your mortgage early may not be the best way to deploy this cash.
For example, a diversified basket of stocks like a low-cost S&P 500 index fund has historically returned better than 4%.
So, if you have the right temperament, you'll likely do better putting your excess cash in stocks than using it to cancel a 4% mortgage.
Also, a well-chosen stock portfolio can give you better diversification than putting all your eggs in your house's equity.
There's also the "optionality" argument:
If you've parked your excess cash in stocks or bonds, you can sell some in case you need the cash later.
But if you've used the excess cash to pay down your mortgage, there's no easy way to get that cash if you're in a pinch.
Also, some mortgages have "early termination" penalties. So there are adverse consequences to paying them off ahead of schedule.
So there may be good reasons not to pay off your mortgage early.
But there are also good reasons *for* paying it off early.
Returns from stocks are uncertain. The 4% you save on mortgage interest is certain.
If seeing big drops in stocks can cause you to panic and make bad decisions, paying the mortgage may be the better option for you.
And there's a certain psychological satisfaction that comes from being debt free.
On paper, your net worth is the same whether you have $100K in assets and zero liabilities, or $200K in assets and $100K in liabilities.
But in real life, many people equate zero debt with a sense of pride, mental well-being, and a life free of financial worry.
At the end of the day, what's "rational" may just be what helps you sleep better at night.
I'll leave you with this message:
The July 4'th weekend is upon us.
In the US, July 4'th is Independence Day.
On the road to Financial Independence, understanding mortgages can be very useful indeed.
Thanks for reading. Stay safe. Enjoy your weekend!
/End