Thread by @polfosol

محور اعداد رو که یادتون هست. حالا فرض کنید داریم رو این محور جلو میریم. بعد هرجا که می‌رسیم به یک عدد اول، این محور می‌پیچه به سمت راست.
مثلا این‌جوری:

۱ از ۶

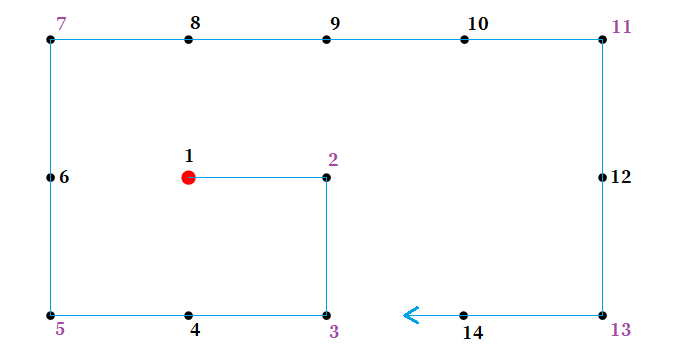
میشه خیلی راحت برنامه‌ای نوشت که به ازای یک عدد نهاییِ دلخواه، این مسیر رو برامون رسم کنه. یه چیزی تو مایه‌های اینی که اینجا نوشتم: bit.ly/2DVwKbK
بعد از ۱۰هزار قدم مسیرمون این شکلی میشه. نقطه شروع در گوشه‌ی سمت راست به رنگ قرمز مشخص شده.

۲/۶

حالا به ازای اعداد مختلف شکل‌های جالبی به‌دست میاد. مثلا شکل سمت چپ تا ۱۰میلیون قدم و سمت راستی تا ۱۰۰میلیون قدم رو رسم کرده:
(نقطه شروع رو هم اگه یه کم بگردید می‌تونید پیدا کنید.)

۳/۶

ولی جالب‌ترینش این شکلیه که بعد از یک میلیون قدم درست شده. روش کلیک کنید تا کاملشو ببینید.
یه جورایی شبیه نقشه قاره آمریکاست. نه؟!

قدرتی خدا 🧐🧐
۴/۶

این شکل‌ها ربط پیدا می‌کنه به توزیع اعداد اول و فواصل بینشون؛ و تقریبا نشون میده که اعداد اول به‌طور رندوم توزیع شدن. هرچند که این مسأله خودش یک قضیه بسیار بسیار مهم تو نظریه اعداده. در اون حد که یک‌میلیون دلار جایزه برای اثباتش تعیین کردن. #جدی

(نظریه ریمان رو سرچ کنید)
۵/۶

اما برای اپیلاسیون تضمینی، بدون لیزر و عوارض جانبی، توصیه می‌کنم این کلیپ رو ببینید که درباره‌ی یک مارپیچ دیگه از اعداد اول توضیح داده. راستش انقدر قشنگ بود که من الان که دیدمش گریه‌م گرفت. دیگه از ذوقم گفتم سر صبحی یه دوخط کد و چندتا توییت بنویسم.

۶/۶