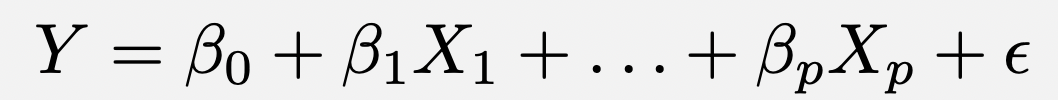Thread by @WomenInStat

Let's extend the linear model (LM) in the directio of the GLM first. If you loosen up the normality assumption to instead allow Poisson, binomial, etc (members of the "exponential family" of distributions), then you can model count, binary, etc responses. (4/)

You've probably heard of Poisson regression or logistic regression. These fall under the umbrella of GLM. (5/)

The LM regression equation is E(Y) = X Beta, where X is the model matrix, Beta is the vector of coefficients, Y is the response vector, and E(Y) is the expected val.

For Poisson regression, we have log(E(Y)) = X Beta.
For logistic regression, we have log(p/(1-p))= X Beta (6/)

Where log is the natural log, and p is the probability of 'success' (whatever that means in your context).

As you can see the right hand side (RHS) of the regression equation is the same but the LHS is changing to go from LM to GLM. (7/)

We HAVE to do this because the RHS of the equation covers the whole real line (-infty, infty) while E(Y) where Y~Pois only covers the positive half of the real numbers and p covers only the interval [0,1]. (8/)

The function on the LHS is called the link function: it's a component-wise, monotone function that maps E(Y) to the real numbers (-infty, infty). (9/)

There are other link functions beyond what is listed here, but I just wanted to give you some concrete examples.

Now we have covered LM --> GLM.

Next, let's go LM --> LMM. (10/)

Imagine we are back in the land of LM and you have a factor (categorical variable) with 100 categories. For ex, maybe you have 100 people in your study and you measure each person several times.

You know there's person-to-person differences. One (naive) way to account ... (11/)

...for these differences is to make Beta (the coefficients vector) really big: give each person their own intercept.

Yikes, now you have a lot of parameters to estimate! This could be problematic with degrees of freedom. (12/)

To help with the estimation problem, we can make those intercepts into "random effects" (mean 0 random variables, which are often normally distributed).

Instead of estimating each intercept, we can instead estimate the variance of the random effects. (13/)

Your random effects could all have the same variance, or you could have a couple variances (e.g. one variance for the Europeans and another for the Asians).

Thus we have swapped out 99 fixed effects for one (or a few) variances. This estimation problem is nicer! (14/)

To remind you, we have turned some components of Beta into random effects. The ones that are still in Beta are called "fixed effects."

We say we have a linear "mixed model" because there's a combo of fixed effects and random effects. (15/)

Introducing these random effects helps us loosen the assumption of independence. The components of Y are no longer independent. However, the components of Y **conditional on the random effects** ARE independent in the LMM. (16/)

To get back to the big picture, we have moved from LM to GLM and separately we have moved from LM to LMM.

As that cute kid says, "why not both?"

We can have both random effects and a response from an exponential family. That's a GLMM. (17/)

In other words, we can add random effects to a Poisson regression.

We can also add random effects to a logistic regression.

These would be examples of GLMM. (18/)

And now my 1 PM meeting starts so sit tight and digest the last 18 tweets!

HALF TIME BREAK.