Thread by @mribeirodantas

1/18 Eu costumo assistir o @sharktankbrasil e, em um episódio que assisti hoje, topei mais uma vez com um termo que tá na boca do povo mais do que nunca, principalmente por causa da #COVID19: Crescimento exponencial.

Vamos lá bater um papo em um fio🧶sobre curva exponencial? 😁

2/18 A primeira informação que talvez surpreenda algumas pessoas é a seguinte: NÃO, a curva de casos de COVID19 *NÃO TEM CRESCIMENTO EXPONENCIAL*. E não tem porque é impossível que tivesse. Isso torna menos assustador? *NÃO, NÃO TORNA*. Com essas duas informações postas, sigamos.

3/18 Vc deve estar se perguntando: “Mas Marcel, por que em todo canto dizia q o crescimento era exponencial se não era?” Bem, existem algumas explicações para isso. A primeira razão é que a palavra exponencial já é um termo popularizado, até por ter significado fora da matemática

4/18 Ou seja, se o objetivo era dizer q o crescimento era fora do comum, muito grande, dizer para as pessoas q ele era exponencial foi um modo de garantir q todo mundo entenderia a gravidade do problema. No entanto, o discurso costumava ser técnico, de divulgação científica, e

5/18 isso acabou fazendo uma confusão, porque várias pessoas confundiram um crescimento grande com o crescimento exponencial de fato, no sentido matemático/científico. Mesmo recentemente me deparei com textos técnicos onde utilizavam uma curva exponencial para fazer esse ajuste.

6/18 O segundo ponto é q epidemias costumam ter crescimento exponencial, mas *no início*. Em Abril, ainda no começo da pandemia, escrevi sobre “A matemática promissora por trás do ‘achatamento da curva’”. Ali, já trazia a função logística, + adequada.

https://twitter.com/mribeirodantas/status/1254325100482113539

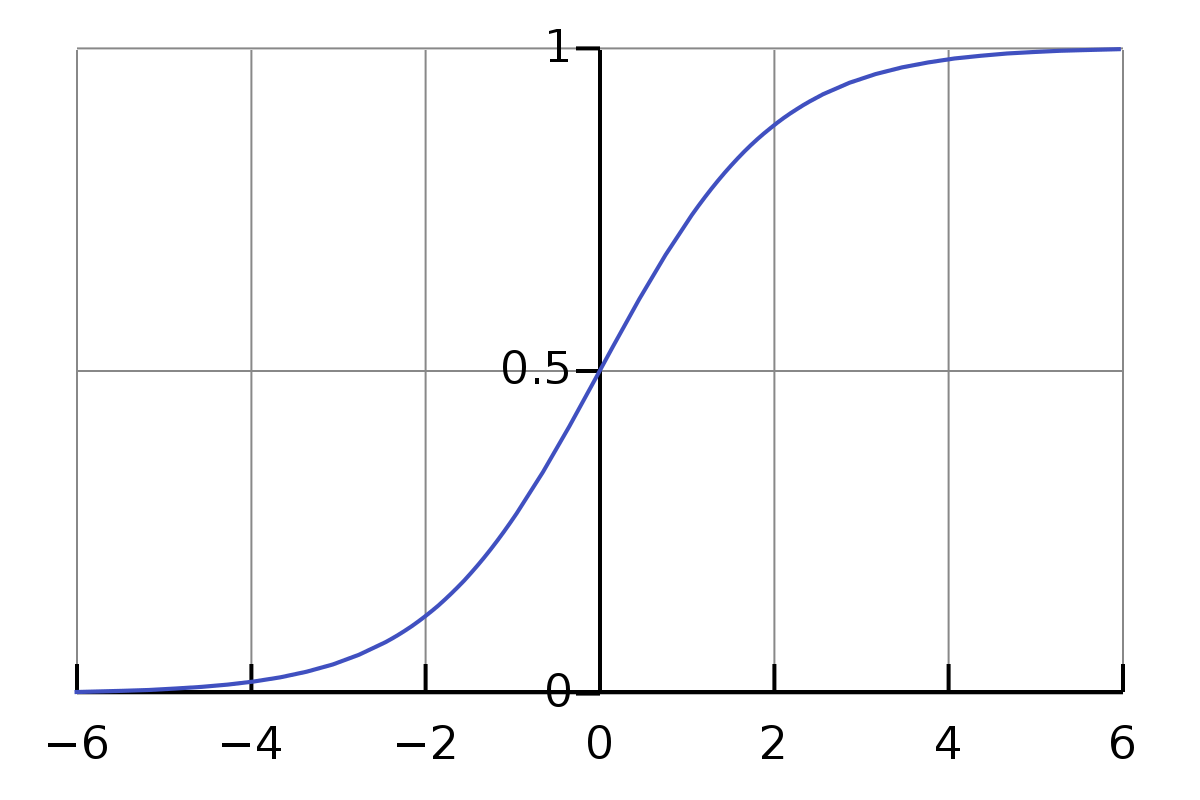
7/18 Lá nos primeiros tweets desse 🧶, falei q era impossível a função ser exponencial. Por quê? No eixo vertical acima, temos o número de pessoas. Se a função fosse de fato exponencial, precisaríamos ter infinitas pessoas, o que não é possível. O q acontece, na verdade, é um

8/18 crescimento próximo de exponencial NO INÍCIO, seguido de uma desaceleração até q o crescimento é praticamente interrompido. Pq? Pq não tem praticamente mais ninguém p/ infectar. Seja pq todos foram a óbito, sobraram apenas imunes, o vírus ficou isolado em uma região, etc.

9/18 Ou seja, no começo onde supostamente todos somos suscetíveis à infecção, o crescimento é muito + rápido. Mas com pessoas já doentes, já imunes, já mortas, isoladas, medo, máscara, higiene, etc, é natural q o vírus tenha mais dificuldade em se alastrar c/ a mesma velocidade.

10/18 Observem o gráfico abaixo para o Rio Grande do Norte, retirado de covid.lais.ufrn.br/#taxa-rt, por exemplo. Em Fevereiro, no começo da pandemia, a taxa estimada de transmissibilidade (ou reprodutibilidade) chegou a 15. Desde então despencou, mas ainda assim fica em torno de um

11/18 número, crescendo ou diminuindo, dependendo do comportamento da população (isolamento, higiene, etc). Não ter um crescimento exponencial em todo o intervalo da doença significa que o crescimento é menos assustador? Como já disse, não. Observe as funções abaixo, por exemplo.

12/18 A função exponencial é a curva verde. Como vocês podem ver, de início, as outras funções são + assustadoras mas por volta da segunda semana a exponencial se torna de fato mt pior e c/ o tempo isso se torna absurdo. Mas assim como poderíamos ter uma outra função exponencial

13/18 como 3 elevado a x, ou 10 elevado a x, também poderíamos ter outras funções não exponenciais tão assustadoras quanto nesse período da imagem. No dia 9, nós temos f(x) = 2^9 que é 512 (na exponencial). Uma função f(x)=x^10, por sua vez, no mesmo período, seria quase 3.5

14/18 bilhões, metade da população do planeta. Mesmo uma função cúbica (x elevado à terceira potência, x^3), nos daria f(x)=x^3=9^3=729. Pior que a exponencial 2^x, percebem? No começo da pandemia, em alguns lugares, vimos algo parecido com essa f(x)=2^x. 2 pessoas, e então 4, 8

15/18 16,32,64,128. se essa fosse de fato a função de todo o período de infecção, quantas pessoas supostamente estariam infectadas 30 dias depois? Mais de um bilhão de pessoas. E 3 dias depois? Mais de 8 bilhões, ou seja, mais pessoas do que existe na terra. No final das contas,

16/18 existem duas informações q gostaria q vc tenha compreendido: (1) “Modelos exponenciais relativos a fenômenos físicos só podem se aplicar a regiões previamente delimitadas, já que um modelo com crescimento infinito não é fisicamente realístico.” pt.wikipedia.org/wiki/Crescimen…

17/18 Ou seja, ñ, a curva de casos da COVID FELIZMENTE ñ tem crescimento exponencial. E (2) poderíamos ter tido um crescimento q é ñ exponencial, e ainda assim, pior do q o q observamos. Assim como poderíamos ter tido algo diferente caso as pessoas tivessem se comportado de modo

18/18 diferente. Como divulgador científico, tento evitar utilizar termos que tem significados diferentes no dia a dia das pessoas e na ciência (como teoria, exponencial, lei, etc). E quando o faço, deixo claro qual significado estou utilizando. Fica de sugestão para os colegas!