
Vamos a introducirnos en el mundo de la Dinámica No Lineal, Caos y Bifurcaciones.
El mapa logístico es un Sistema No Lineal que trata de describir la evolución de una determinada población, aunque ciertas soluciones parecen extrañas.
Veamos por qué esto es así.
El mapa logístico es un Sistema No Lineal que trata de describir la evolución de una determinada población, aunque ciertas soluciones parecen extrañas.
Veamos por qué esto es así.
En primer lugar, definimos los términos que aparecen en el modelo.
- xn es la proporción entre la población existente y la población máxima que puede llegar a haber (varía entre 0 y 1)
- r es un coeficiente que captura efectos de reproducción y mortalidad (potencial biótico)
- xn es la proporción entre la población existente y la población máxima que puede llegar a haber (varía entre 0 y 1)
- r es un coeficiente que captura efectos de reproducción y mortalidad (potencial biótico)
Como se puede observar, según el valor de r la solución del sistema puede ser muy distinta.
Una bifurcación ocurre cuando las soluciones de un sistema dinámico cambian cualitativamente por la variación de algún parámetro. Exploremos las distintas soluciones del mapa logístico.
Una bifurcación ocurre cuando las soluciones de un sistema dinámico cambian cualitativamente por la variación de algún parámetro. Exploremos las distintas soluciones del mapa logístico.
En primer lugar, para valores de r entre 2.5 y 3, la población evolucionará a una única población de equilibrio.
En este rango, esta solución es la única posible y el sistema no podrá tender a ningún otro valor en esta región.
En este rango, esta solución es la única posible y el sistema no podrá tender a ningún otro valor en esta región.

Para valores de r algo mayores que 3, el aspecto de las soluciones cambia completamente. Se produce una bifurcación donde aparecen dos ramas nuevas.
En este caso, la población oscilará de un valor a otro de manera continua y ya no hay un único valor de equilibrio.
En este caso, la población oscilará de un valor a otro de manera continua y ya no hay un único valor de equilibrio.

Si seguimos subiendo r aparecen dos nuevas bifurcaciones.
Esto significa que, ahora, la población irá alternando entre 4 valores distintos a lo largo de tiempo, aunque seguimos conociendo con precisión cuáles son estos cuatro valores entre los que alternará.
Esto significa que, ahora, la población irá alternando entre 4 valores distintos a lo largo de tiempo, aunque seguimos conociendo con precisión cuáles son estos cuatro valores entre los que alternará.

Y, si seguimos aumentado r, llegamos al CAOS.
En esta región del diagrama, las poblaciones varían de una manera muy grande de un año a otro, siendo en la práctica imposible determinar cuál será la población al año siguiente por la gran sensibilidad que tienen estas ecuaciones.
En esta región del diagrama, las poblaciones varían de una manera muy grande de un año a otro, siendo en la práctica imposible determinar cuál será la población al año siguiente por la gran sensibilidad que tienen estas ecuaciones.

No es que el sistema sea aleatorio, ya que conocemos las ecuaciones y es completamente determinista.
Pero debido a la gran sensibilidad de las ecuaciones a condiciones iniciales, en la práctica, cualquier pequeño error de precisión numérica conducirá a soluciones distintas.
Pero debido a la gran sensibilidad de las ecuaciones a condiciones iniciales, en la práctica, cualquier pequeño error de precisión numérica conducirá a soluciones distintas.
De hecho, para generar número aleatorios, John von Neumann propuso utilizar el mapa logístico para un valor de r = 4, ya que justo para este valor el rango de valores que se pueden obtener varía entre 0 y 1.
Esta disciplina de la dinámica no lineal es tremendamente complicada y realmente se ha podido desarrollar y avanzar mucho más en ella gracias al aumento de la potencia de los ordenadores.
Su uso es prácticamente obligatorio para este tipo de sistemas.
Su uso es prácticamente obligatorio para este tipo de sistemas.
Para fijar esta idea de las bifurcaciones, veamos el problema del pandeo.
Una viga en vertical, a la que se le coloca una masa pequeña encima, lo normal es que no sufra pandeo. A medida que se aumenta la masa, se llega a un valor crítico a partir del cual la viga pandea.
Una viga en vertical, a la que se le coloca una masa pequeña encima, lo normal es que no sufra pandeo. A medida que se aumenta la masa, se llega a un valor crítico a partir del cual la viga pandea.
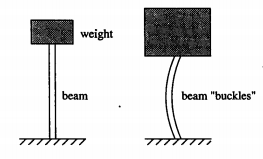
Aquí se puede ver el diagrama de bifurcación donde el parámetro es la masa sobre la viga y phi es el ángulo con la vertical.
Como se ve, a partir de la carga crítica, las soluciones estables (a las que tenderá el sistema) son las de pandeo. La solución nula es inestable.
Como se ve, a partir de la carga crítica, las soluciones estables (a las que tenderá el sistema) son las de pandeo. La solución nula es inestable.

Pronto traeré más animaciones sobre este tipo de sistemas, dado que son mucho más comunes de lo que podríamos pensar, además de sumamente interesantes.
Mientras, podéis ver un ejemplo de sistema caótico en la animación del péndulo doble que ya realicé.
Mientras, podéis ver un ejemplo de sistema caótico en la animación del péndulo doble que ya realicé.
https://twitter.com/RayleighLord/status/1294704772914778112?s=20
• • •
Missing some Tweet in this thread? You can try to
force a refresh


