Thread by @stanislavfort

Excited to share our new #neurips2020 paper /Deep learning versus kernel learning: an empirical study of loss landscape geometry and the time evolution of the Neural Tangent Kernel/ (arxiv.org/abs/2010.15110) with @KDziugaite, Mansheej, @SKharaghani, @roydanroy, @SuryaGanguli 1/6

We Taylor-expand Deep Neural Network logits with respect to their weights at different stages of training & study how well a linearized network trains based on at which epoch it was expanded. Early expansions train poorly, but even slightly into training they do very well! 2/6

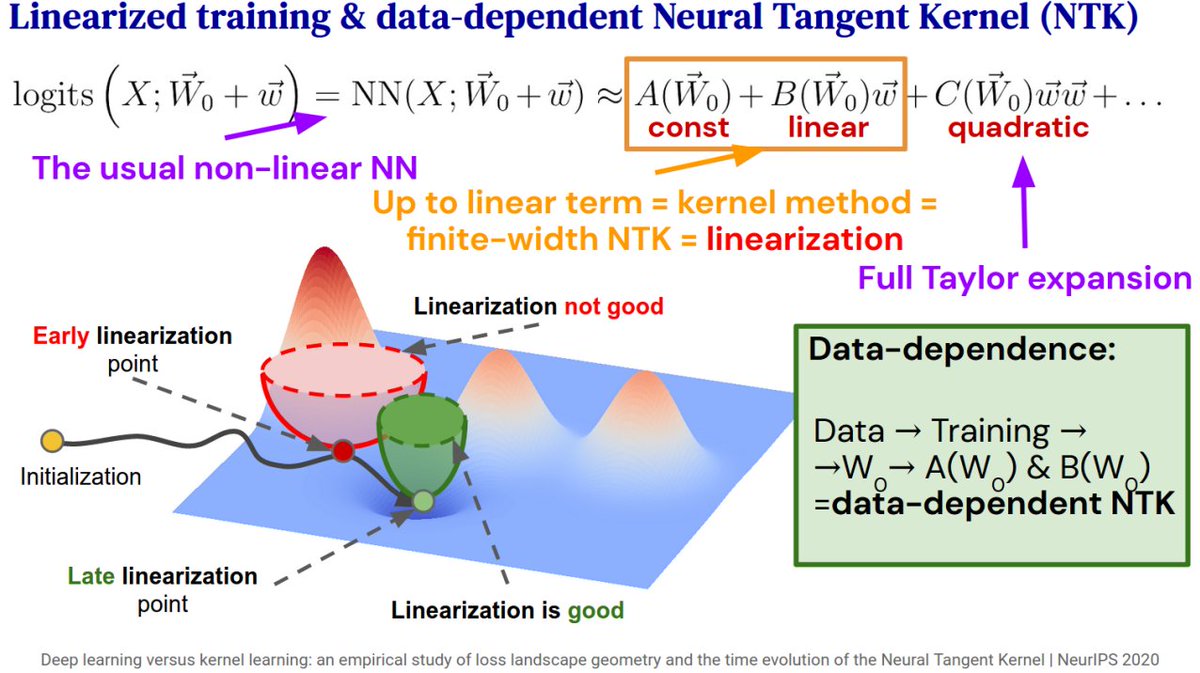
Linearized DNNs underperform compared to even low learning rate trained nonlinear networks, but only for expansions /very early/ in training. We call this the *nonlinear advantage* and show that it disappears quickly into training. 3/6

Surprisingly, the nonlinear advantage a DNN enjoys over its linearized counterpart seems to correlate well with the error barrier (=instability in arxiv.org/abs/1912.05671 @jefrankle @mcarbin) between 2 NNs trained from that point, connecting two very different concepts. 4/6

We find that many other DNN measures such as function space distance (similar to arxiv.org/abs/1912.02757 @balajiln), kernel distance, logit gradient similarity (similar to arxiv.org/abs/1910.05929) and others correlate in a similar manner. 5/6

It seems that the importance of the nonlinear nature of deep neural nets is crucial at the beginning of training, but diminishes relatively soon after that, where Taylor expanded DNNs (even 1st order, in the ∞-width regime=Neural Tangent Kernel) perform almost equally well. 6/6

This was joint work with an amazing team of @KDziugaite @mansiege @SKharaghani, @roydanroy, @SuryaGanguli