Thread by @genkuroki

#統計 「伝統的な統計学」について、Fisher's exact testに関わるゴタゴタもウンザリさせられるような事態になっている。

* 2×2の分割表のχ²検定はFisher検定の近似に過ぎないので、可能ならば正確なFisher検定の方を使うべきだ(特に度数が小さい場合には)。

このデタラメを他人に教える人が多過ぎ。

#統計 一応念のためため述べておきますが、私は統計学についてはど素人。

そして、数学に関係した事柄については「教科書に書いてある」とか「査読論文に書いてある」のような事実を正しいことの証拠に挙げる人達を常日頃から「権威に基づいて正しさを判定するろくでもない奴らだ」と言っています。

#統計

⭕️2×2の分割表のχ²検定の方法をサンプルサイズが大きな場合のFisher検定の近似によって導出できる。

という主張は正しいです。しかし、

❌χ²検定はFisher検定の近似としてしか導けない。
❌Fisher検定は正確である。
❌χ²検定の誤差をFisher検定との違いで測るのが正しい。

はどれも誤り。

#統計 2×2の分割表のFisher検定が正確でないことは、コンピュータで以下を確認すればすぐに分かります。

* 固定された超幾何分布に従ってランダムに生成した2×2の分割表のP値がα未満になる確率がほとんどの場合にαより大幅に小さくなること。

* 特にサンプルサイズが小さい場合にそれは悪化する。

#統計 添付画像は a+b=7, c+d=13, a+c=9 を満たす分割表

a b
c d

の超幾何分布について、P値がx未満になる確率のグラフです。P値がx未満になる確率はxに一致して欲しいのですが、全然そうなっていない。

Fisher検定は強い有限離散性が原因でひどく不正確になります。

gist.github.com/genkuroki/085e…

#統計 a+b=7, c+d=13, a+c=9 を満たすサイズ20の超幾何分布に従うサンプルの場合には、Fisher検定において有意水準5%で第1種の誤りが生じる確率は1.7%を切っています(5%に近い方がよい)。

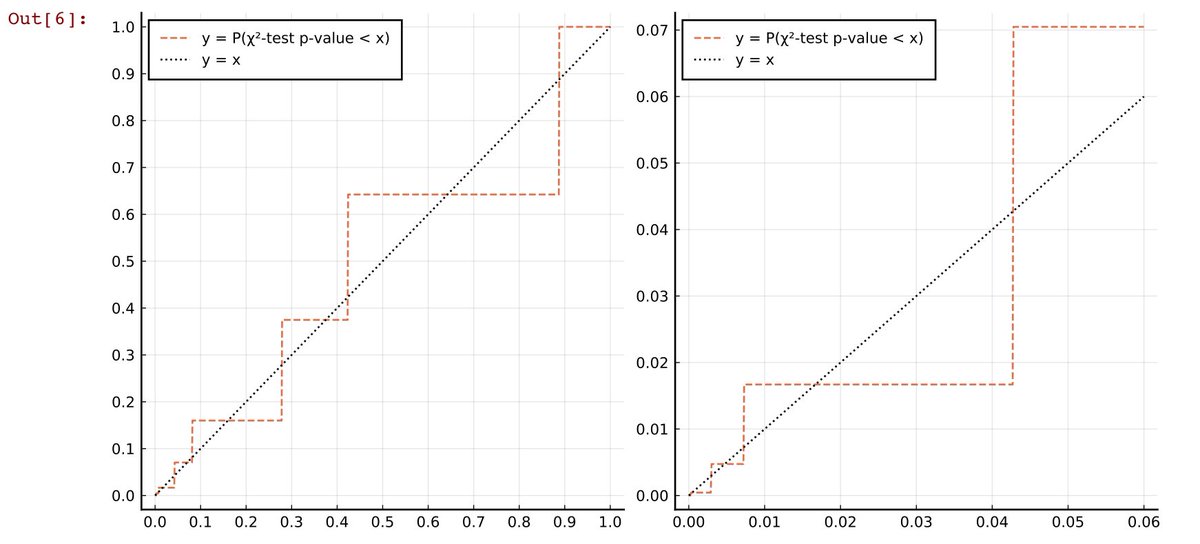
#統計 添付画像は、a+b=7, c+d=13, a+c=9 を満たすサイズ20の超幾何分布に従うサンプルの場合の、χ²検定のP値がx未満になる確率のグラフです。

45度線に近いと正確なのですが、そこから大きく外れており、しかも有意水準5%で第1種の誤りが生じる確率は7%を超えている。

gist.github.com/genkuroki/085e…

#統計 a+b=7, c+d=13, a+c=9 を満たすサイズ20の超幾何分布に従うサンプルの場合の、χ²検定のP値がx未満になる確率のグラフだけを見ると、小サンプルにおいてχ²検定はひどく不正確で使うべきではないという俗説を信じてしまうかもしれない。

しかし、それは短慮であり、間違っています。

#統計 現実に得られる分割表

a b
c d

のデータを得るときには、周辺度数 a+b, c+d, a+c, b+d のすべてを固定することは通常不可能です。

現実には、分割表のデータは、予算の都合である期間内に得られた事例を集めたものかもしれない。その場合には周辺度数は何1つ固定されなくなる。続く

#統計 添付画像は、そのような周辺度数が何1つ固定されない場合(サンプルが独立性の帰無仮説を満たすPoisson分布の直積で生成されている場合)に、P値がx未満になる確率をプロットしたものです。a+b+c+dの期待値は20．

45度線に近い検定がより正確。

gist.github.com/genkuroki/085e…

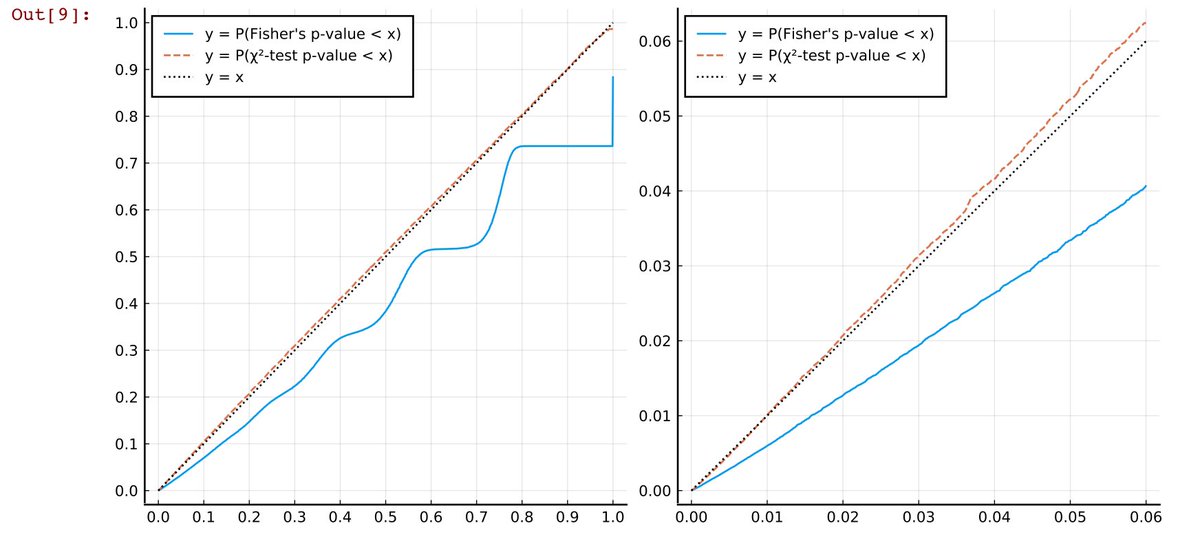
#統計 a+b+c+dの期待値が20という小サンプルの場合に、データの生成のされ方についてより現実的な想定をしたならば、Fisher検定はひどく不正確であり、χ²検定の方がずっと正確であることが分かりました。

Fisher検定が正確だと書いてある教科書は間違っています。

#統計 以上の計算で使った #Julia言語 カーネルのJupyter notebook を

gist.github.com/genkuroki/085e…

で公開してあります。

そこで採用した数値を色々変えれば、特に小サンプルにおいてFisher検定は常にひどく不正確で、χ²検定は概ね正確である極端な場合にのみひどく不正確になることを確認できます。

#統計 第1種の誤りの確率を名目有意水準より確実に小さくしたい場合にはFisher検定を使う価値がありますが、有望そうな知見を得るために使う場合には無用に検出力を下げてしまっているので注意が必要。

χ²検定は実際にコンピュータで確認すると想像以上に悪くない検定法であることも分かります。

#統計 私が #Julia言語 を使ってやったのと同じことを #R言語 でやりたい人は、Rのchisq.testがデフォルトでYates補正を入れてしまうことに注意を払う必要があります。

私が十分に正確であることを確認したχ²検定は補正なしのカイ検定です。Yates補正を入れるとFisher検定よりも不正確になります。

#統計 率直に言って、2×2の分割表について「Fisher検定は正確である」とか「χ²検定はYates補正を入れるべきである」と他人に教えている人達は社会的に負の貢献をしていると思います。

教科書や講義に騙されて、教わったデタラメを次世代に伝える加害者側に転じている。

#統計 非常に残念なことに統計学は「お墨付きを得るための道具」として使われてしまっているだけではなく、2×2の分割表の独立性検定でχ²検定を使っている無実の人に対して、論文のレフェリーが教科書に載っている間違った考え方でいちゃもんを付けるというようなことが起こっているのではないか？

#統計 実際には、統計学を使った報告を行うところまで来れた人は論文のレフェリーに文句を言われずに済むように教科書の間違った説明に従うというようなことを行なっている場合が多いでしょう。

中には、面倒になって有益な知見を含むかもしれない報告をやめてしまう人もいるかもしれません。

#統計 2×2の分割表の独立性に関する自由度1のχ²検定は、χ²検定の全体の基礎になっている非常に一般的な定理であるWilks' theoremから直接的に出ます。超幾何分布を経由する必要はありません。

Wilks' theoremについては私の過去ツイートを参照
twilog.org/genkuroki/sear…

コンピュータで遊べるネタ

https://twitter.com/genkuroki/status/1325757353250095105

#統計 サンプルが独立性の帰無仮説を満たす各種の分布で生成されているときに、Fisher検定のP値がx未満になる確率がx以下になることの証明は、独立性の帰無仮説を満たす各種の分布の条件付き確率分布として超幾何分布が出て来ることから得られます。続く

#統計 Fisher検定の理解を「サンプルのランダム化」という発想で済まそうとしている人達は不十分な理解にしか到達できません。条件付き確率分布として超幾何分布が出て来ることを経由したFisher検定の正当化についてもどこかで学ぶ必要があると思います。(私は自分で考えた。)

#統計 2×2の分割表の独立性のFisher検定やχ²検定については、実践的にも理論的な理解についても、おかしな考え方をよく見かけます。

2×2の分割表の独立性検定は頻出の道具なので頭の痛い問題だと思います。

伝統的な教科書に書いてあるおかしな説明をそのまま次世代に伝える行為はやめるべき。

#統計 Yates補正がダメなことについては以下のリンク先スレッドを参照。Yatesさん自身が1984年の論文にダメなことを書いているという事実を紹介しています。

https://twitter.com/genkuroki/status/1197290460294733824

#統計 私は統計学の専門的訓練を受けた経験が皆無のど素人に過ぎません。この点に注意して読むよう、お願い致します。

素人なので証拠に当たる情報は可能な限り出すようにしています。

例えばコンピュータを使った場合にはソースコードを全開示している。

#統計 Fisher検定に付随する適切な信頼区間の話

Rでfisher.testを使うとP値と整合性のない不適切な信頼区間も表示されるのですが、Fisher検定に付随する適切な信頼区間の定義を知るためには、P値と信頼区間の表裏一体の関係を理解する必要があります。

#統計 P値はモデルMとデータDで決まります。モデルがパラメータθで決まるとき、P値はパラメータθとデータDの函数だとみなせる。

データDから得られるパラメータθの信頼係数1-αの信頼区間を「P値がα以上になるパラメータθの範囲」と定義すると非常に便利です。

これをFisher検定でどう実装するか？

#統計 超幾何分布は期待値のオッズ比ωをパラメータに持つFisherの非心超幾何分布のω=1の場合に一致。

超幾何分布から作られる2×2の分割表AのP値は、Fisherの非心超幾何分布の場合に容易に一般化可能です。

これで、パラメータωと分割表AにP値を対応させる函数が得られ、ωの信頼区間も得られる。続く

#統計 以上のストーリーにおけるFisher検定におけるP値函数と信頼区間函数は #Julia言語 ならば実質1行で書けます。詳しくは以下のリンク先を参照。

https://twitter.com/genkuroki/status/1316291214891606016

#統計 χ²検定における期待値のオッズ比ωのP値函数と信頼区間函数を定義するためには、Wilks' theoremを使う議論(最尤法の計算)をやり直す必要がある。

Wilks' theoremを使わずに超幾何分布経由でχ²検定を理解することにこだわると、こういうこともできなくなります。Wilks' theoremは基本中の基本。

https://twitter.com/genkuroki/status/1196022252598251521

#統計 #R言語 でデフォルトで使える fisher.test や binom.test が表示する信頼区間は表示されるP値と整合性がないので要注意。

どうしてそういう仕様にしているのか、私には理解不能。

おそらく「伝統に根差すろくでもない考え方」が原因だと思う。

みんな使っているソフトでさえ信用し切れない。

#統計 データDから得られるパラメータθの信頼係数1-αの信頼区間を「P値がα以上になるパラメータθの範囲」と定義すると、多くの場合に教科書に書いてある標準的な信頼区間の定義に一致します。

この新たな信頼区間の定義はおそろしくクリアです。

続き

#統計 信頼区間の意味が分かりにくいのはこの定義を説明してくれないからだと思う。

αが有意水準なら、信頼度1-αの信頼区間は「検定で棄却されないパラメータθの範囲」でしかない。

使用したモデルについてパラメータθがこの範囲に入っていることを覚悟せよ、のような使い方をできる。

#統計 信頼区間の復習

モデルM(θ) (θ∈Θ) のデータDに関するP値がpval(θ, D)のとき、データDから得られる信頼係数1-αの信頼区間ci(α, D)は

ci(α, D) = { θ∈Θ | pval(θ, D) ≥ α }

と定義される。αが有意水準のとき、

ci(α, D) = (データによって棄却されないパラメータθの範囲)

になる。

#統計 信頼度1-αの信頼区間ci(α, D)は、データDとP値函数pval(θ, D)によって有意水準α棄却されないモデルM(θ)のパラメータθの範囲なので、信頼区間を「その範囲にパラメータが入っている可能性が高い範囲」と安易に解釈してはいけないことが分かる。

#統計 モデルM(θ)のデータDに関するP値は「モデルM(θ)内でデータD以上に偏った状態が生じる確率の近似値」として定義してやる。P値函数の定義は「モデルM(θ)」「データD以上に偏った状態」の定義と「モデルM(θ)内における確率の計算法」に依存して決まる。

#統計 こんな感じで、一般的なP値や信頼区間の定義を正確にした後では、P値や信頼区間の数学的定義から導出不可能な結論を俗説に従って出すことを防ぎ易くなる。

統計学を「お墨付きを得るための道具」として使って来た人達は「俗説」が通用しなくなると困るに違いない。科学的には困る方がよい。

#統計 データとP値函数によって棄却されないモデルM(θ)の範囲をパラメータθの範囲で表示したものが信頼区間。

パラメータ値θでモデルM(θ)が棄却されないことは、検定のイロハより、パラメータ値θでのモデルM(θ)が確からしいことを意味しません。

こういうことを正確に議論することが大事。

#統計 統計学の「お墨付きを得るための道具」としての地位を守るために様々な「哲学っぽい響きを持つ俗説」を持ち出す議論はすべてずさんであり、まじめに相手をできるような議論にはなり得ません。

#統計 統計学がどのような数学的道具を利用しているかを明確にし、その数学的道具から導出できない結論を丁寧に排除して行くと、統計学が恐ろしく困難な不良設定問題を扱うために巧妙に作られた素晴らしい道具であることがより見え易くなります。

安易な俗説の使用は微妙な点を見えなくしてしまう。

#統計 1つ前のツイートのような言い方をすると、私の実際の感覚よりずっと堅苦しく聞こえてしまう。

このスレッド全体を眺めれば分かるように、コンピュータを気軽に使える現代においては、統計学で使われている数学的道具の性質をコンピュータによるシミュレーションを楽しみながら確認できます。

相互リンク

https://twitter.com/genkuroki/status/1327826340616183808

#統計 このスレッドに関係した事柄を私以外の人による解説で読みたい人には

jstage.jst.go.jp/article/dds/30…

がお勧め(添付画像)。

引用【いずれの手法にも一長一短があり、データ解析者は、よりよい判断をくだすために、適用する手法の特徴を十分に理解し、データの様相をよく観察せねばならない】

https://twitter.com/genkuroki/status/1195564328734191616