Thread by @quantian1

It's been a while since I've done one of these, but on paper many of you are following me (why?) because of quant finance tweets, so let me do a rambling stream-of-consciousness apologia for the most hated "model" in finance, the Black-Scholes model.

Specifically, the idea of IV. Like "imaginary numbers", it's an unfortunate misnomer, because it makes people think there must be *some* link between IV and historical vol. This is not the case. A better term might be something like "σ-price" vs. "$-price": it's a price.

Option prices trend in predictable ways: a near-term option will always be cheaper than a long-term one, simply because the long-term one includes the near term one. Similarly, ITM options are always more expensive than OTM options, because they contain the OTM option as well.

This is annoying to deal with, because sometimes you want to compare different options in a way that corrects for this: is it "cheaper" to buy a 1y option that's out of the money or a 6m option that's ITM? We would like to transform the price in such a way that corrects for this.

If you look at a (vanilla) option, most things about it are known and fixed: you know the strike (K), you know the current price (S), you know when it expires (T), etc. Now, like any good modeler, you just need a fudge factor X that will let you fit the price of the option (C/P).

What properties would we like X to have? Certainly there should be a 1:1 map between X and C/P, so we can go back and forth without loss of information. We would also like X to be insensitive to changes in things like K and T, so we can compare different options on even ground.

Since this is purely a fudge factor, it could be anything we like. For a call, we could say something like "X = (C-max(S-K,0))/S", so now we're backing out the baked-in payoff of the call and normalizing by price. This is good, but we can do better.

We could plot a bunch of ATM option prices and note that they tend to increase like sqrt(T), so if we divided by that to normalize for T, we would do even better- adding a prefactor (for reasons we will get to soon), and now "X=2.5C/S/sqrt(T)". This fits data quite well!

However, let's do one better. If you are a fancy mathematician, you might look at this and say "this is nice but it's very ad-hoc, let's try and derive a model compatible with it." Now we enter into the land of Scary Math- let's puzzle out what minimal assumptions we can add.

0. The stock price is a nonnegative random process
1. We know what the stock price is today
2. We hope moves on one day don't really affect moves on other days
3. We think our initial uncertainty doesn't vary over time
4. Over most tiny time intervals, the stock doesn't move

Note that I am not yet making assumptions about things like market structure or aggregate Gaussian behavior or anything! Just the above five assumptions! In fact, given assumption 0 (stochasticity+log space), we can rewrite 1-4 quite precisely as using fancy math as follows:

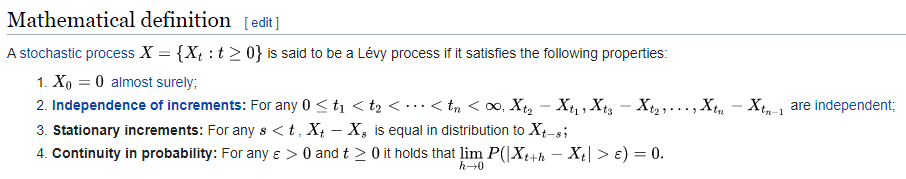
These four assumptions lead us to a surprisingly wide class of choices called "Lévy Processes". These include things like Brownian motion, but also jump models, stable distributions, Poisson queues, etc. There is now also a very powerful theorem we can apply to our problem.

This is called the Lévy-Khintchine Representation, and it stats that any Levy process can be written as the sum of three things:
A. Deterministic linear drift
B. Brownian noise
C. Large "jumps" that happen randomly and "rarely" (in technical terms, on a set of measure 0)

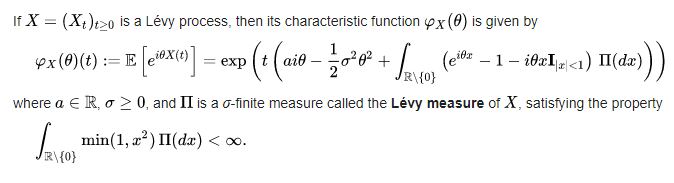
We have meandered around for a while and are getting no closer to an answer, so let's cut to the chase: If we said at this point we wanted to get the "simplest" possible model, we'd ditch C and keep A/B. This now gives us a continuous model with no jumps.

At this point, the problem is now determined. By enforcing nonnegativity and continuity, the only Levy process left is one where log(S) is a Brownian motion-- the Black-Scholes model. Our fudge factor X is now the square root of the variance of our Brownian motion--the IV.

"But Quantian," you whine pathetically. "Some Arab guy in a Mini Cooper said the normal distribution is bad!!" OK, fine. Pick any other continuous distribution with a location and shape parameter--Laplace or whatever--and you can derive a corresponding option pricing formula.

After adding in your no-arbitrage condition to replace the location parameter, you get a similar 1:1 relationship between the option price and an "implied shape parameter." The math can be tricky, but it still works. You can even go out and trade options based off it if you like!

[Aside: It still works in *most* cases. There's a technical restriction on how fat tails can be, namely that E[e^tX], the moment generating function of the distribution you pick, must be finite near 0. That means Cauchy is out, and your tails must go to 0 faster than O(x^-n)]

But here's the problem: By switching to a non-normal density, your Lévy-Khintchine representation now has jumps again. This is problematic, because random jumps of random size mean you can't figure out how to hedge an option anymore- if you calculate greeks, they'll be messed up.

So, if you actually have a book of options you want to figure out how to usefully hedge, the only assumption that will give you a good result is continuity. You can still trade options in a discontinuous world, but hedging is a bitch and must be done via other options.

That's what IV is: it's the "correct" pricing transform fudge factor, in the simplest possible model that gives useful results. You can use this to plot things like volatility surfaces, which show in a normalized fashion which options are cheap vs. expensive and also look cool.

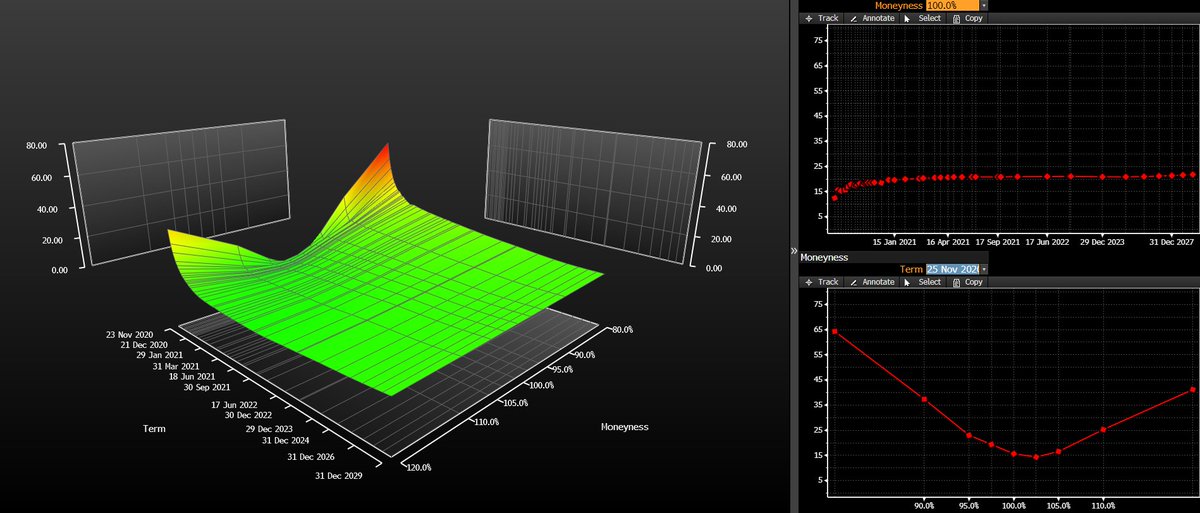
This is where most actual research is focused: what does a "true" volatility surface look like? How can it best be calibrated? How do you properly match things like index vol vs. derivative vol (SPX/VIX calibration problem). It's not about trying to find the "correct" $-price.

In conclusion: to quote the Veb account quoting the cursèd chipmunk account, "Calculating something 'as if' it were normally distributed is epistemologically distinct from calculating something and assuming that it's normally distributed, because the as-if is now nonparametric"

If you would like to learn more about this, please ask my large son, @ONAN_OUS, who used to do this at his old job. If you are about to attack me for being grievously wrong in an arcane assumption above, you're either @bennpeifert or @highermoments, please have mercy on me. FIN.