Thread by @AlejandroPiad

Today is #TheoryThursday 🧐!

The most important question in all of Computer Science is probably whether P equals NP. That is, are all problems easy to validate also easy to solve?

How can we even start to ponder this question? 🧵👇

🔖 In case you're just hearing about this, here's a short refresher on what we are talking about:

https://twitter.com/AlejandroPiad/status/1316706290345873408

Let's think now about what would it mean to properly answer this question. 👇

Say we want to answer "yes". How can we do that? Do we have to check that *all* NP problems are actually in P?

👉 To begin, there are infinitely many problems in Computer Science.

There must a better way...

🤔 What if we could prove that just answering yes to *one problem* would automatically answer yes to *any other problem*?

Imagine that, a CS problem that would represent them all, such that solving that problem would immediately give you a solution to any other (NP) problem.

Say we have two problems A and B. For example, say A = sorting an array (SORT), and B = finding the minimum element (MIN).

How can we prove that B is at least as easy as A? In other words, if we have a polynomial algorithm for solving A, we must also have one for solving B. 👇

What we need is a polynomial-time reduction from B to A. This sounds complicated, but it's very intuitive.

👉 What we want is a way to implement MIN provided that you can call SORT, and that implementation has to be of polynomial complexity. For example:

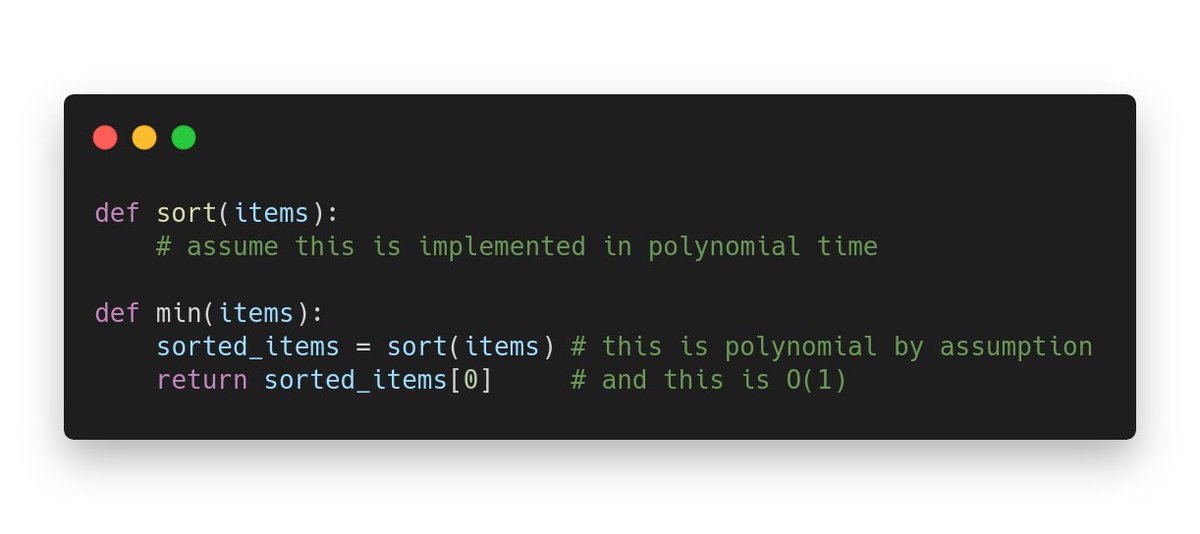
Now we can definitely say that MIN is at least as easy as SORT. Maybe it's even easier (and we know it is, you can solve MIN in O(N) and SORT only in O(N log N) in the general case).

🔑 The question now is, can we do this with one problem A for all other problems B (in NP)?

It turns out, this is exactly what Stephen Cook and Leonid Levin, independently, both showed around the 1970s.

But how does this work? What does it mean to find such a problem? 👇

The problem in question is Boolean Satisfiability (SAT), and it works like this:

❓ Given a Boolean formula, with variables and Boolean operators, such as *x & y | z*, is there any assignment of True/False to each variable that makes the formula true?

Sometimes the formula is extremely easy, but when it involves several copies of the same variable, some positive and some negative, it is not trivial to, just looking at the formula, decide if it's satisfiable.

👉 However, it is very easy to validate, so SAT is clearly in NP.

🤔 Now, how can you go on proving that SAT is a problem to which any other problem in NP is polynomially-reducible?

First, remember we are concerned *only* with decision problems, i.e., problems whose answer is True or False.

Here are some intuitions... 👇

Say we have a decision problem B that is in NP. This means there is a polynomial algorithm V to verify if a solution of B for a specific input I is indeed True.

🤯 We can create a Boolean formula F that basically says "B answered True to input I", for every possible input I.

This formula is quite large, but it is always possible to build it for a specific input I, by using the code of the verification algorithm.

☝️ That means (believe me here) that the formula remains polynomial with respect to the length of I.

👉 An intuitive way to see that such a formula must be possible to build is to consider that whatever V is, it is a program composed at the end of a bunch of basic instructions.

☝️ We can always build a formula, in principle, that says "this instruction was executed" and so kind of trace the execution of V in a Boolean form.

Formally, this is done with the Turing-machine definition of V, but intuitively, think of it as disassembling the code of V.

For any input I, we can build in polynomial time a formula F whose satisfiable iif B would answer True to I.

We can then run SAT(F), and we have a polynomial-time solution for B(I).

⭐ And that's it! We have one problem, SAT, that can solve any other problem in NP.

This problem, SAT, is the first of the so-called NP-Complete problems.

A problem in NP that is so general, that any other problem in NP could be solved in polynomial time if you could solve that one problem.

But is not the only one! 👇

The most surprising finding is not SAT itself, but rather that is there is a huge number of such problems, seemingly very different, but in their core all equivalent:

🔹 Traveling salesman
🔹 Scheduling
🔹 Knapsack
🔹 Clique
🔹 Graph coloring
🔹 Hamiltonian cycles
🔹 ...

As usual, if you like this topic, reply in this thread or @ me at any time. Feel free to ❤️ like and 🔁 retweet if you think someone else could benefit from knowing this stuff.

🧵 Read this thread online at <apiad.net/tweetstorms/th…>

Stay curious 🖖:

📚 <dl.acm.org/doi/10.1145/80…>
📚 <people.eecs.berkeley.edu/~luca/cs172/ka…>
📄 <en.wikipedia.org/wiki/Cook%E2%8…>
📄 <en.wikipedia.org/wiki/Karp%27s_…>
🎥 <>