Is this formula difficult? π€
This is the formula for Gradient Descent with Momentum as presented in Wikipedia.
It may look intimidating at first, but I promise you that by the end of this thread it will be easy to understand!
Thread π
This is the formula for Gradient Descent with Momentum as presented in Wikipedia.
It may look intimidating at first, but I promise you that by the end of this thread it will be easy to understand!
Thread π
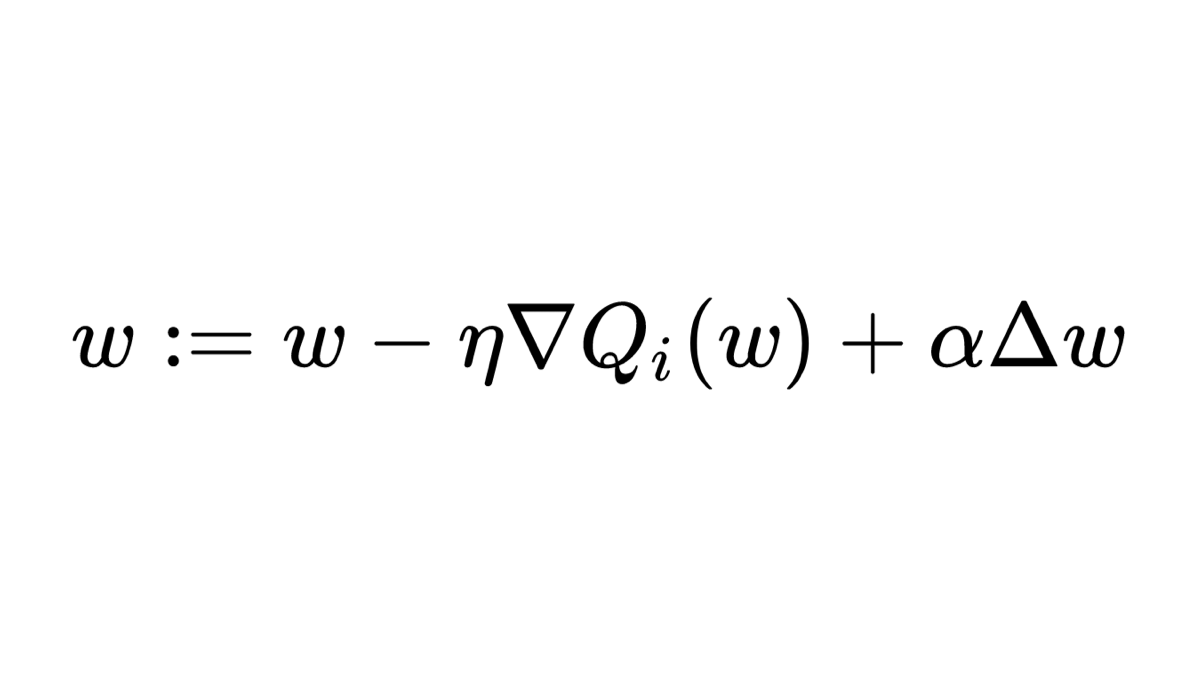
The Basis β»οΈ
Let's break it down! The basis is this simple formula describing an iterative optimization method.
We have some weights (parameters) and we iteratively update them in some way to reach a goal.
Iterative methods are used when we cannot compute the solution directly
Let's break it down! The basis is this simple formula describing an iterative optimization method.
We have some weights (parameters) and we iteratively update them in some way to reach a goal.
Iterative methods are used when we cannot compute the solution directly
Gradient Decent Update π
We define a loss function describing how good our model is. We want to find the weights that minimize the loss (make the model better).
We compute the gradient of the loss and update the weights by a small amount (learning rate) against the gradient.
We define a loss function describing how good our model is. We want to find the weights that minimize the loss (make the model better).
We compute the gradient of the loss and update the weights by a small amount (learning rate) against the gradient.
Here is an illustration how it works.
The gradient tells us if the loss will decrease (negative gradient) or increase (positive gradient) if we increase the weight.
The learning rate defines how far along the gradient we will jump in the current step of the optimization.
The gradient tells us if the loss will decrease (negative gradient) or increase (positive gradient) if we increase the weight.
The learning rate defines how far along the gradient we will jump in the current step of the optimization.
Momentum β½οΈ
Now we add the momentum. It is defined as the weight update in the previous step times a decay factor.
The decay factor is just a number between 0 and 1 defining how much of the previous update will be taken into account. Ξ± = 0 means no momentum and Ξ± = 1 is a lot.
Now we add the momentum. It is defined as the weight update in the previous step times a decay factor.
The decay factor is just a number between 0 and 1 defining how much of the previous update will be taken into account. Ξ± = 0 means no momentum and Ξ± = 1 is a lot.
A useful analogy is a ball rolling down a hill. If the hill is steep, the ball will accelerate (we update the weights more).
This will help the ball jump over small local minima and continue down the hill (to a smaller loss).
More momentum means a heavier ball with high inertia
This will help the ball jump over small local minima and continue down the hill (to a smaller loss).
More momentum means a heavier ball with high inertia
Putting it all together π
So, in the original formula we update the weights using two terms.
The *gradient descent* term pushes us down the slope of the loss function.
The *momentum* term helps us accelerate and jump over small local minima.
Not that hard, right? π
So, in the original formula we update the weights using two terms.
The *gradient descent* term pushes us down the slope of the loss function.
The *momentum* term helps us accelerate and jump over small local minima.
Not that hard, right? π
β’ β’ β’
Missing some Tweet in this thread? You can try to
force a refresh
γ
