#Julia言語 10行では無理なやつ
正方形上の自由境界条件の波動方程式の離散化をDifferentialEquations.jlで数値的に解いて動画を作ってみた↓
nbviewer.jupyter.org/gist/genkuroki…
これを作るために必要な行数は40行程度でした。
正方形上の自由境界条件の波動方程式の離散化をDifferentialEquations.jlで数値的に解いて動画を作ってみた↓
nbviewer.jupyter.org/gist/genkuroki…
これを作るために必要な行数は40行程度でした。
https://twitter.com/genkuroki/status/1373559550805118982
#Julia言語 約1万個の質点がバネで繋がっている状況を記述する常微分方程式 prob を DifferentialEquations.jl に sol = solve(prob) の形式で数値的に解かせています。自分でソルバを書かなくて良いとかなり楽です。
nbviewer.jupyter.org/gist/genkuroki…
nbviewer.jupyter.org/gist/genkuroki…
#Julia言語 正方形ではなく、正五角形上の自由境界条件のもとでの波動方程式の数値解。
これもDifferentialEquations.jlを使っています。
コードの効率はそうよくないのですが、シンプル。

これもDifferentialEquations.jlを使っています。
コードの効率はそうよくないのですが、シンプル。


#Julia言語 正五角形上の自由境界条件のもとでの波動方程式の数値解の動画。値がNaNだと作画しないことを使っています。
実際には23729個の質点がバネで繋がっている状況の運動方程式をDifferentialEquations.jlで数値的に解いています。
こういうことがシンプルなコードで可能。
実際には23729個の質点がバネで繋がっている状況の運動方程式をDifferentialEquations.jlで数値的に解いています。
こういうことがシンプルなコードで可能。
#Julia言語 ソースコード↓
nbviewer.jupyter.org/gist/genkuroki…
In[4]より前の部分は準備です。
以下の添付画像中の解説を見てから、In[4]より前の部分を見た方が多分楽に解読できる。
これと似たような時間で重力で相互作用している300体問題の数値解を求められると思います。誰かやらないかな?
nbviewer.jupyter.org/gist/genkuroki…
In[4]より前の部分は準備です。
以下の添付画像中の解説を見てから、In[4]より前の部分を見た方が多分楽に解読できる。
これと似たような時間で重力で相互作用している300体問題の数値解を求められると思います。誰かやらないかな?

#Julia言語 #数楽 こういう動画を作るときには、境界での値が固定されるディリクレ境界条件よりも、境界での値もびらびら動くノイマン境界条件の方が見た目的に面白い動画が出来上がります。
境界条件は私のコードでは力(もしくは加速度)を記述する函数 g! の定義の中に自然に組み入れられている。
境界条件は私のコードでは力(もしくは加速度)を記述する函数 g! の定義の中に自然に組み入れられている。
#数楽 用意した配列の数十%を無駄に使っている点がちょっと気になったので、五角形版のコードを書き直しました。
数値解の計算が12~13秒程度から7~9秒程度に高速化。
2万数千個の質点がそれぞれ隣の質点とバネで接続されている系
ゆっくり版動画も作った。
nbviewer.jupyter.org/gist/genkuroki…
数値解の計算が12~13秒程度から7~9秒程度に高速化。
2万数千個の質点がそれぞれ隣の質点とバネで接続されている系
ゆっくり版動画も作った。
nbviewer.jupyter.org/gist/genkuroki…
#Julia言語 整理したので微分方程式の記述(特に g!)がものすごくシンプルになりました。
複雑なことはモデルのパラメータの情報が全て格納してあるMy.Param型変数 p にすべて押し付けられています。
「モデル・問題→数値解」の流れはよくある典型的パターンの1つ。
nbviewer.jupyter.org/gist/genkuroki…
複雑なことはモデルのパラメータの情報が全て格納してあるMy.Param型変数 p にすべて押し付けられています。
「モデル・問題→数値解」の流れはよくある典型的パターンの1つ。
nbviewer.jupyter.org/gist/genkuroki…

#Julia言語 非常によく見る悪習の1つ(おそらく大学教育で広めている)に、「モデル・問題→解」の形式にコードを整理せずに、
❌モデルのパラメータを大域変数の形式でべたがきして、
解を求める函数の中で使うこと
があります。
Juliaとこの悪習の相性は最悪。
Juliaでなくてもひどいと思う。
❌モデルのパラメータを大域変数の形式でべたがきして、
解を求める函数の中で使うこと
があります。
Juliaとこの悪習の相性は最悪。
Juliaでなくてもひどいと思う。
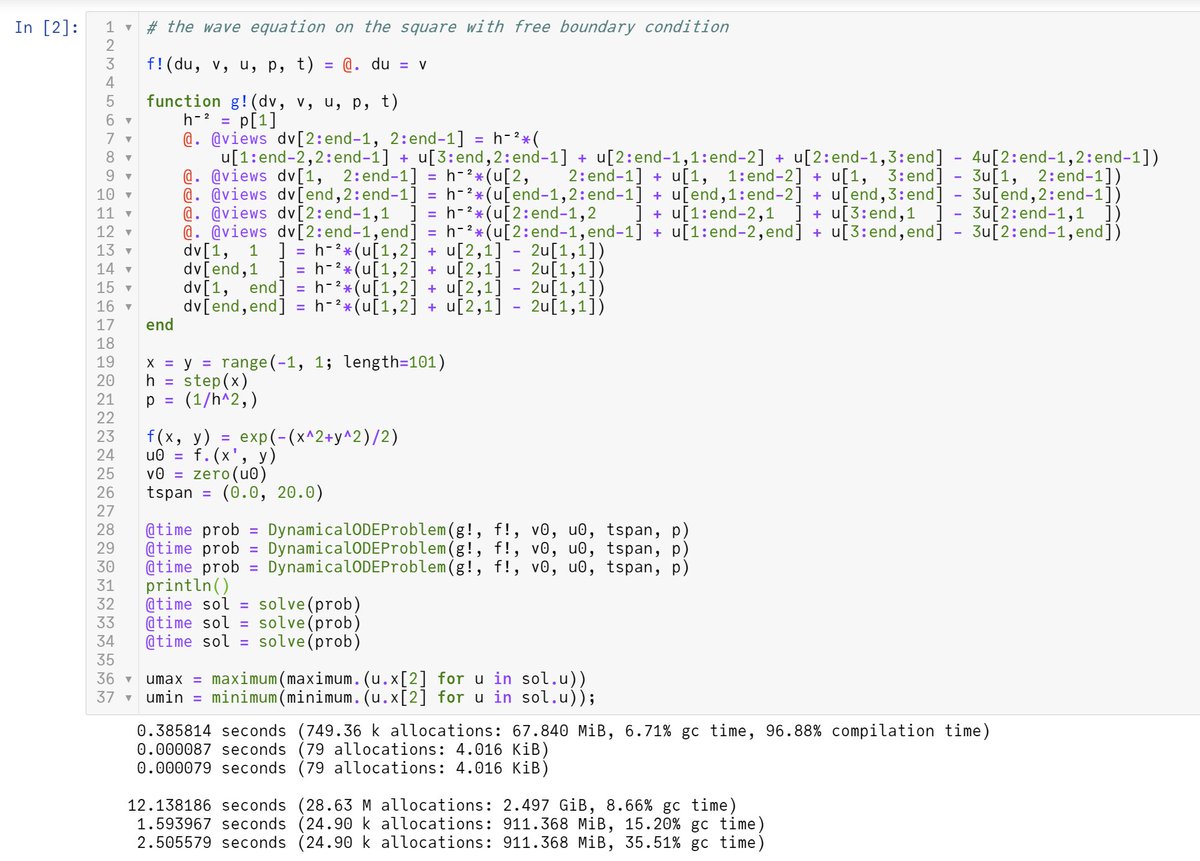
#Julia言語 添付画像のコード
⓪ p = My.Param(~)の行でモデル記述に使われる情報が1変数にまとめられている。
① prob = DynamicalODEProblem(~)の行でモデル全体の情報が1変数にまとめられている。
② sol = solve(prob)の行で問題を解いている。
これがJuliaでのよくあるパターンです。
⓪ p = My.Param(~)の行でモデル記述に使われる情報が1変数にまとめられている。
① prob = DynamicalODEProblem(~)の行でモデル全体の情報が1変数にまとめられている。
② sol = solve(prob)の行で問題を解いている。
これがJuliaでのよくあるパターンです。

#Julia言語 複数の函数で複数のパラメータの値を共有したいことはよくあります。
Juliaでは共有したいパラメータをグローバル変数に入れておくのはアウト。計算速度が落ちる。
共有したいパラメータをconstにすることもお勧めできません。それをやってしまうと、パラメータの型が変更不可能になる。
Juliaでは共有したいパラメータをグローバル変数に入れておくのはアウト。計算速度が落ちる。
共有したいパラメータをconstにすることもお勧めできません。それをやってしまうと、パラメータの型が変更不可能になる。
#Julia言語 constは型を変更不可能なので、constを使っていると、試行錯誤の過程でJuliaを立ち上げ直す回数が大幅に増えます。
共有したいパラメータを1つの変数にまとめて、パラメータを共有したい函数に常にその変数を引数として渡す方が結果的に全体の手間は減ります。
共有したいパラメータを1つの変数にまとめて、パラメータを共有したい函数に常にその変数を引数として渡す方が結果的に全体の手間は減ります。
#Julia言語 そのときに便利なのがParameters.jlパッケージの@ unpackマクロ。
共有したい情報が含まれている変数(一般のstructまたはNamedTupleなど)から
@ unpack x, y, V, E = p
のような形式で情報を取り出せます。
函数中にこの行があれば、どの共有情報をその函数で使っているかが分かる。
共有したい情報が含まれている変数(一般のstructまたはNamedTupleなど)から
@ unpack x, y, V, E = p
のような形式で情報を取り出せます。
函数中にこの行があれば、どの共有情報をその函数で使っているかが分かる。
#Julia言語 「解きたい問題を記述する十分な情報は何か?」「問題を記述している情報からどのようにして問題を解くか?」を考えることをコードを書く前に当然やっているはずなのに、それをそのままプログラムとして記述せずに、グローバル変数に問題記述のパラメータをべたがきするのはおかしい。
#Julia言語 ノイマン境界条件(端の動きが自由)の場合から、ディリクレ境界条件(端が固定)の場合に変更するためには、微分方程式を記述している函数 g! をほんの少し書き変えるだけで済みます。
添付画像①②を比較してみて下さい。
nbviewer.jupyter.org/gist/genkuroki…

添付画像①②を比較してみて下さい。
nbviewer.jupyter.org/gist/genkuroki…


#Julia言語 これで(かなり手抜きになってしまいますが)、任意の形状の領域上での波動方程式の数値解をDifferentialEquations.jlで得る方法が分かりました。
添付画像はノイマン境界条件の正五角形の場合。しっかり境界が固定されています。
添付画像はノイマン境界条件の正五角形の場合。しっかり境界が固定されています。
#Julia言語 定義域が制限されている2変数函数のグラフをプロットするときには、値がNaNの部分がプロットされないというPlots.jlの仕様を使うと良いです。
#Julia言語 以上では私が好きだという理由で正五角形上の波動方程式を扱いましたが、正五角形は任意の領域に容易に置き換えられます。
添付画像はアニュラスの場合(ノイマン境界条件)
nbviewer.jupyter.org/gist/genkuroki…
添付画像はアニュラスの場合(ノイマン境界条件)
nbviewer.jupyter.org/gist/genkuroki…
#Julia言語 アニュラスの場合には94232個の質点がバネで繋がった系で離散化を行っています。離散化で得られた常微分方程式をDifferentialEquations.jlでさくっと数値的に解いている。
DifferentialEquations.jlを使う場合にはJulia v1.6以上を推奨。私はnightly build
nbviewer.jupyter.org/gist/genkuroki…
DifferentialEquations.jlを使う場合にはJulia v1.6以上を推奨。私はnightly build
nbviewer.jupyter.org/gist/genkuroki…
#Julia言語
g_dirichlet!のコード中の -(4 - length(E[k])) * u[k] の項が、0に固定されている境界と u[k] を繋ぐバネ(自然長は0)から来る力を与えている。(E[K]はu[k]とバネで繋がっているu[j]の全体。2次元格子上の領域では4以下になる。)
これがディリクレ境界条件の離散化の仕組み。
g_dirichlet!のコード中の -(4 - length(E[k])) * u[k] の項が、0に固定されている境界と u[k] を繋ぐバネ(自然長は0)から来る力を与えている。(E[K]はu[k]とバネで繋がっているu[j]の全体。2次元格子上の領域では4以下になる。)
これがディリクレ境界条件の離散化の仕組み。
https://twitter.com/genkuroki/status/1373947827244597251

#Julia言語 #数楽
質点どうし及び質点と固定端がバネで繋がった系での力は
m_k d²u_k/dt²
= 質点kと繋がった質点j達との間のバネから来る質点kへの力
+ (もしもあるなら)質点kと固定端の間のバネから来る力
と書ける。m_k=1でバネ定数がh⁻²の場合のJulia語への翻訳が添付画像の枠内のコード。
質点どうし及び質点と固定端がバネで繋がった系での力は
m_k d²u_k/dt²
= 質点kと繋がった質点j達との間のバネから来る質点kへの力
+ (もしもあるなら)質点kと固定端の間のバネから来る力
と書ける。m_k=1でバネ定数がh⁻²の場合のJulia語への翻訳が添付画像の枠内のコード。

#Julia言語 添付画像枠内のコードを見れば分かるように、微分方程式を扱うコード自体は質点と質点及び固定端がバネで繋がった系一般を扱うことができている。
この部分は大学新入生レベルの物理で非常に易しい。
その易しい物理をほぼそのままJulia語に直訳できている点が重要なポイント!
この部分は大学新入生レベルの物理で非常に易しい。
その易しい物理をほぼそのままJulia語に直訳できている点が重要なポイント!

#Julia言語 問題をコンピュータに与えるときには、数学や物理の教科書にあるような記述をほぼそのまま見易く直訳した形式で与えることができた方が便利。
添付画像のコードでは実際にそれに成功している。
初期条件の形状も函数f(x,y)で見やすく与えられている。
添付画像のコードでは実際にそれに成功している。
初期条件の形状も函数f(x,y)で見やすく与えられている。

#Julia言語
膜の形状を記述して、離散化するコードも書かなければいけない。(高級なことを一切せず、素朴にやっている。)
まず、膜の形状を記述する函数を書いた。
点が正五角形に含まれるかどうかを判定する函数。
この函数は振動する膜と無関係の数学的函数。
nbviewer.jupyter.org/gist/genkuroki…
膜の形状を記述して、離散化するコードも書かなければいけない。(高級なことを一切せず、素朴にやっている。)
まず、膜の形状を記述する函数を書いた。
点が正五角形に含まれるかどうかを判定する函数。
この函数は振動する膜と無関係の数学的函数。
nbviewer.jupyter.org/gist/genkuroki…

#Julia言語 離散化はx軸とy軸を等間隔で離散化することによって行う。Julia語では区間[a, b]を両端のa,bも含めてN+1個に等分する点の全体は
range(a, b; length=N+1)
と書ける。
x = y = range(-1, 1; length=201)
の第10行はx軸とy軸の離散化を行なっている。
range(a, b; length=N+1)
と書ける。
x = y = range(-1, 1; length=201)
の第10行はx軸とy軸の離散化を行なっている。

#Julia言語 x軸とy軸を離散化すれば、平面の格子状の離散化が得られる。格子点が隣の格子点とバネで繋がっている状況で連続的な膜を近似する。
そのような格子点達がバネで繋がったものを正五角形型に切り取れば、正五角形型の膜の離散化が得られる。
こういう思考は心の中では一瞬で終わる。続く
そのような格子点達がバネで繋がったものを正五角形型に切り取れば、正五角形型の膜の離散化が得られる。
こういう思考は心の中では一瞬で終わる。続く
#Julia言語 直観的なイメージで一瞬で終了するほど易しい考え方をすることはとても重要。
何をやればいいのか難しく感じる場合には、自分自身が難しく考えてしまっていること自体が原因であることが実に多い。
一瞬で終わるほど易しく考えることができたなら、それをコードに翻訳することも易しい。
何をやればいいのか難しく感じる場合には、自分自身が難しく考えてしまっていること自体が原因であることが実に多い。
一瞬で終わるほど易しく考えることができたなら、それをコードに翻訳することも易しい。
#Julia言語
* 点(x,y)が膜上の点であるかどうかを判定してくれる函数
* x軸とy軸の離散化
が与えられたら、
* 膜上も格子点全体の集合 V
* 膜上の各格子点がどの格子点と繋がっているかを記述するデータ E
を作る函数を作れば、膜の振動を大量のバネの振動に近似的に帰着できる。
* 点(x,y)が膜上の点であるかどうかを判定してくれる函数
* x軸とy軸の離散化
が与えられたら、
* 膜上も格子点全体の集合 V
* 膜上の各格子点がどの格子点と繋がっているかを記述するデータ E
を作る函数を作れば、膜の振動を大量のバネの振動に近似的に帰着できる。

#Julia言語 そのときに、膜に含まれる格子点の配列Vを作ることは、膜上の格子点に1,2,…と番号をつけることに等しい。膜上も格子点から逆にその番号を得るための辞書V_dicも作っておくと便利である。 

#Julia言語
(u(x+h, y) - u(x,y)) + (u(x-h) - u(x,y) ≈ u_{xx}(x, y)h²
なので、uのxによる2階の偏微分は
u_{xx}(x, y) = h⁻²((u(x+h, y) - u(x,y)) + (u(x-h) - u(x,y))
と書ける。x軸とy軸の離散化での刻み幅をhとしたとき、連続極限を取るためには、バネ定数をh⁻²にすれば十分である。
(u(x+h, y) - u(x,y)) + (u(x-h) - u(x,y) ≈ u_{xx}(x, y)h²
なので、uのxによる2階の偏微分は
u_{xx}(x, y) = h⁻²((u(x+h, y) - u(x,y)) + (u(x-h) - u(x,y))
と書ける。x軸とy軸の離散化での刻み幅をhとしたとき、連続極限を取るためには、バネ定数をh⁻²にすれば十分である。

#Julia言語 微分方程式として扱う場合には、膜内の格子点の個数分だけの自由度を持つ系として扱われ、初期条件を与えたり、数値解を視覚化するときには、xy平面上の格子の上での値を並べた行列としての記述が使われる。
それぞれのサイズを length, sizeとして定義しておいて、利用することにする。」
それぞれのサイズを length, sizeとして定義しておいて、利用することにする。」

#Julia言語 自由度の長さを持つベクトルuとしての記述と、格子点上での値を記述する行列Uとしての記述を、行ったり来たりする函数を vec2mat, mat2vec として作っておく。 

#Julia言語
Juliaでは一般に、返り値がベクトルや行列になる函数を作るときには、すでに用意してあるベクトルや行列の成分として返り値を返す in-place 型の函数(名前の最後に!を付ける習慣)を経由するとよい。
添付画像のコードもそのようにしてある。
Juliaでは一般に、返り値がベクトルや行列になる函数を作るときには、すでに用意してあるベクトルや行列の成分として返り値を返す in-place 型の函数(名前の最後に!を付ける習慣)を経由するとよい。
添付画像のコードもそのようにしてある。

#Julia言語 【重要❗️】
新たにベクトルや配列を作ってメモリ割当を引き起こす函数をループの内側で使うと、メモリ割当に分量が爆発する場合がある。
すでに確保されたベクトルや配列を作業領域として使い回す函数を用意しておけば、そのようになることを防げる。
docs.julialang.org/en/v1/manual/p…
新たにベクトルや配列を作ってメモリ割当を引き起こす函数をループの内側で使うと、メモリ割当に分量が爆発する場合がある。
すでに確保されたベクトルや配列を作業領域として使い回す函数を用意しておけば、そのようになることを防げる。
docs.julialang.org/en/v1/manual/p…
#Julia言語 【重要❗️続き】
そのための用心として、返り値がベクトルや行列になる関数のコードを書く場合には、"pre-allocating output" を行う "in-place" 型の函数を先に用意して、それを経由するように書いた方が安全である。
(このスレッド内の目的のためには無用の用心)
そのための用心として、返り値がベクトルや行列になる関数のコードを書く場合には、"pre-allocating output" を行う "in-place" 型の函数を先に用意して、それを経由するように書いた方が安全である。
(このスレッド内の目的のためには無用の用心)
#Julia言語 以上の解説とDifferentialEquations.jlの公式ドキュメントを読めば、膜の振動を扱ったノートブック達
nbviewer.jupyter.org/gist/genkuroki…
nbviewer.jupyter.org/gist/genkuroki…
のコードを完全に理解できると思う。
これを見て自分でも色々やる人が増えると良いと思う。
nbviewer.jupyter.org/gist/genkuroki…
nbviewer.jupyter.org/gist/genkuroki…
のコードを完全に理解できると思う。
これを見て自分でも色々やる人が増えると良いと思う。
#Julia言語 DifferentialEquations.jlのDynamicalODEProblemについては
diffeq.sciml.ai/stable/types/d…
diffeq.sciml.ai/stable/solvers…
を参照。
これは、シンプレクティック法を使いたい場合には(物理的な問題では使いたいことが多い)、特に参考になる情報である!
沢山の方法が実装されている。


diffeq.sciml.ai/stable/types/d…
diffeq.sciml.ai/stable/solvers…
を参照。
これは、シンプレクティック法を使いたい場合には(物理的な問題では使いたいことが多い)、特に参考になる情報である!
沢山の方法が実装されている。



#Julia言語 自分で常微分方程式の数値積分法を実装する経験は必須だと思うが、数値積分法の開発や実装は特別な専門家が必要な分野である。
自分で実装する場合には気をつけないと時代遅れの方法をずっと使い続けるリスクが生じるので注意。
DifferentialEquations.jlを使えばそういうリスクが減る。
自分で実装する場合には気をつけないと時代遅れの方法をずっと使い続けるリスクが生じるので注意。
DifferentialEquations.jlを使えばそういうリスクが減る。
#Julia言語 DifferentialEquations.jlでは函数の引数の順序は概ね次のようになっている。
[微分したもの(dvまたはdu),] [速度 v,] 位置 u, パラメータ p, 時刻 t
例えばハミルトニアン函数は H(v, u, p, t) (pはパラメータ)の形式で作る必要あり。
nbviewer.jupyter.org/gist/genkuroki…
[微分したもの(dvまたはdu),] [速度 v,] 位置 u, パラメータ p, 時刻 t
例えばハミルトニアン函数は H(v, u, p, t) (pはパラメータ)の形式で作る必要あり。
nbviewer.jupyter.org/gist/genkuroki…

• • •
Missing some Tweet in this thread? You can try to
force a refresh