Thread by @capeandcode

If you don't understand the principle of Backpropagation or the notion of the maths behind it.

Then this 🧵 could be helpful for you.

We are going to use a simple analogy to understand better

(Check final tweets for notes)

↓ 1/11

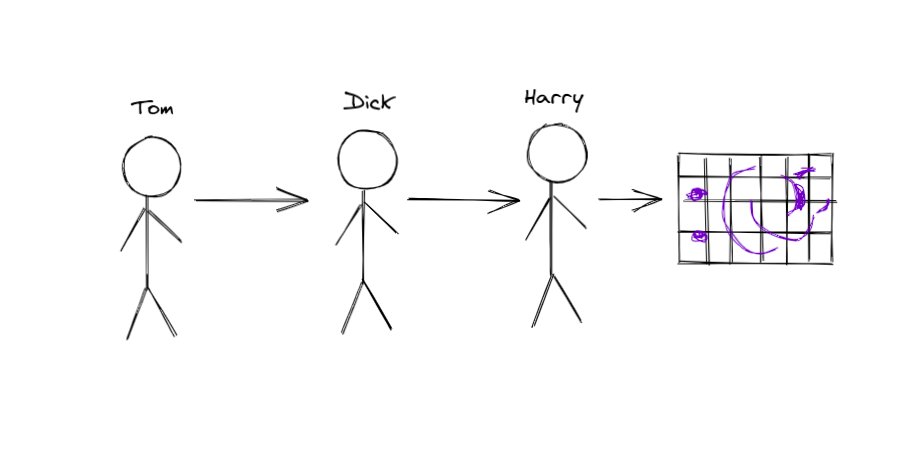
Consider you (Harry) are trying to solve a puzzle along with two of your friends, Tom and Dick
And sadly none of you guys are among the brightest.

But you start trying to put the puzzle together.

2/11

Tom has put the first 6 pieces out of 20, 2 of them are wrong, then passes the puzzle to Dick.
Dick puts the next 8 pieces, 6 of them wrong, then passes the puzzle to you.
And now, you put the final 6 pieces, 4 of them wrong.

The picture is complete.

3/11

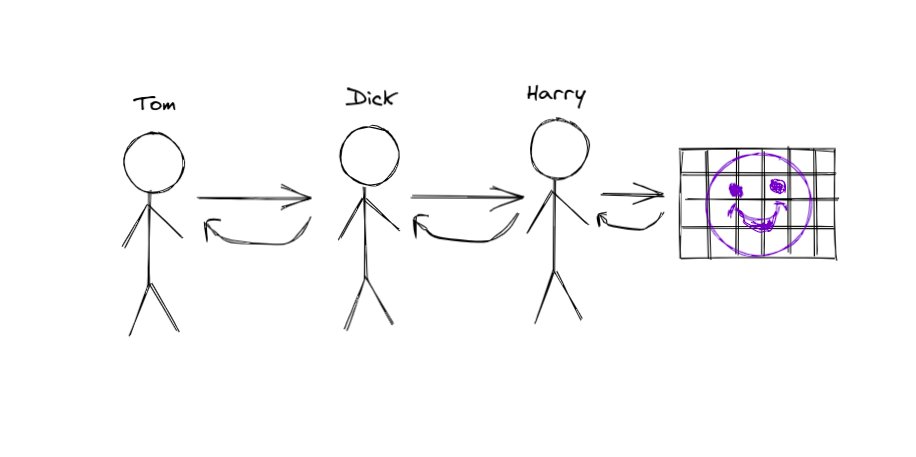
But you look at the instructions and it suggests that you have put 12 pieces wrong.

Now you observe 1/4 of the wrong pieces that you put and correct it, then pass it back to Dick,
Dick corrects 2/8 and lets Tom know,
then Tom corrects 1/2 and asks you to check again.

4/11

Now the manual suggests that you have 8 pieces wrong
So, you repeat the same exercise, until you get it all right, or sufficiently right.

For the process to work the correction has to be communicated from you to Dick to Tom.

How does that explain Backpropagation though?

5/11

🔹Correctly completed Puzzle represents Objective Function
🔹Tom Dick Harry are like 3 layers of NN, Output Layer(Harry), Input Layer(Tom)
🔹The number of wrong pieces is the error we're trying to minimize
🔹Them realizing their mistakes are like the gradients calculated

6/11

Note that, the final error is not dependent only on Harry but also Dick and Tom.

So first Harry corrects himself, then Dick and Tom realize their contribution to the mistake and try to correct it.

7/11

Similarly, once the error has been calculated, the gradient can be directly used to correct the mistakes of
the output layer.

8/11

But since the output is not the direct function of any of the intermediate layers, the error has to be propagated backward through the layers that lie between the output and the corresponding intermediate layer.

9/11

This justifies the use of Chain Rule from Calculus to calculate the partial derivatives.

They help in passing back the respective error gradient to previous layer weights.

10/11

Here's the link for handwritten notes of Backpropagation to understand the mathematics behind better🔣

drive.google.com/file/d/1OwrxOe…

11/11

This example might be an over-simplification but you can get the gist of it.

If you don't get bothered by notations, you'll understand the maths too.

Hope it helps! 👍