Thread by @Manu_M2B

Noo, he vuelto a ver otro RT a esto sin que sepan qué está pasando. Y yo que creía no había bulos en matemáticas... Vamos a ver cómo nos están engañando aquí y, más interesante, si se podría hacer algo así de alguna manera. Dentro hilo🧵

https://twitter.com/Wikingenieria/status/1380918320040439811

Empecemos yendo directos al grano. ¡No se puede hacer algo así! Si lo hiciesemos al revés, siempre podríamos sacar un cuadradito de la nada y me veriais a mí partiendo mis pizzas así para llenarme con solo "un trozo"

Entonces, ¿de dónde sale el cuadrado rojo del final? ¿Han editado el vídeo? ¿Lo hizo un mago?

Pues no, el engaño está en que los dos triángulos no son iguales aunque lo parezcan. Es más, ¡¡este primero ni siquiera es un triángulo!!

Fijémonos en el centro de la imagen, donde los ángulos azul y marrón.

Si esa línea fuese recta, la suma del ángulo azul, el marrón y el ángulo recto de la pieza amarilla sería de 180°. Vamos, que marrón + azul= 90°

Pero fijaos ahora en el triángulo verde. Es rectángulo, así que sus dos ángulos no rectos deben de sumar también 90°. Así que azul + negro=90°.

¡Así que el ángulo marrón y el negro son el mismo!
Si repetimos con el triángulo rojo, nos queda que ambos triángulos tienen los mismos ángulos.

Esto no quiere decir que sean iguales...pero casi. El Teorema de Tales nos dice que en este caso son proporcionales, es decir, que el rojo es igual que el verde pero agrandado.

Pero en el video vemos que no es así, que el pequeño pasa de tener base 4 y altura 2 a tener base 7 y altura 3. No hay ningún número que al multiplicarselo a 2 de 3 y al multiplicarselo a 4 de 7...¡Así que lo que hemos supuesto de que esta linea es recta es falso!

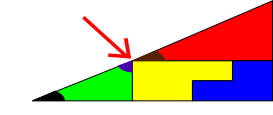
La figura del principio es un cuadrilátero y la del final un triángulo. Y aunque se parecen tanto que a simple vista no las distinguimos, la diferencia es de un cuadrado.

Pero si os lo habíais creído, no os sintáis mal. No sois los primeros ni los únicos. Este tipo de trucos se llaman Paradojas de Disección y tenemos algunas que datan del siglo XVI.

Pero vamos a lo interesante...¿Existe alguna manera matemática de hacer esto y sacar cosas de la nada?

Pues aquí entran los señores Banach y Tarski, que demostraron que se puede partir una bola en pocos cachitos y reensamblarlos en dos bolas idénticas a la original.

Sisi, que formalmente se puede replicar cualquier objeto solo cortándolo unas pocas veces. Pero nunca me verás usar una tijera en un billete, así que vamos a ver cómo también nos la han liado estos dos señores

Hay quien cree que unas matemáticas que permitan esto tienen que ser malas matemáticas, así que rechazan uno de los pilares de la demostración. El axioma de elección.

(Los axiomas son las reglas de base que aceptamos como verdaderas y a partir de ahí construimos todas las matemáticas que conocemos.)

Este axioma dice, así por encima, que si tenemos un armario con infinitas camisetas, cada día podemos escoger una de entre todas ellas sin problema.
Si crees que no se puede hacer esto, estas de suerte, en tus matemáticas no aparecen cosas de la nada.

Pero hay matemáticos que, por gusto por la moda o por no querer comerse la cabeza, quieren poder elegir. En este caso se libran de que en el mundo real se puedan replicar cosas a machetazos porque algunas de las piezas cortadas tienen que ser no medibles.

¿Qué es eso? Pues que son piezas que tienen área...¡pero que es imposible calculara!
Me parece a mí que esos bichos no existen en la vida real, podemos estar tranquilos.

Así que, si os volvéis a encontrar con un video en el que aparezcan cosas de la nada, buscad el truco. Porque las matemáticas pueden ser muy raras, pero nunca nunca engañan.

@threadreaderapp unroll