
References first. There’s really one that’s central for this discussion, this seminal 1973 masterwork from Cheng and Prusoff. 2/
sciencedirect.com/science/articl…
sciencedirect.com/science/articl…
Customary math alert: some high school algebra ahead, but nothing too hefty. Will also have a couple of graphs to illustrate some principles. 3/ 

Let’s start with the IC50. This is bread-and-butter pharmacology. The IC50 (inhibitory concentration 50) is defined as the drug concentration at which the response in a given assay is half-maximal, i.e., 50%. 4/
Graphically it looks like this. A semilog plot of response vs. log dose customarily gives a sigmoidal curve, defined by its max, min, slope (the Hill slope or coefficient), and inflection point. 5/ 

(Aside: the Hill slope has nothing to do with hilly appearances. It’s named after Archibald Hill, a pioneer in enzyme kinetics who developed the dose-response equation, which became known as the Hill equation.) 6/
en.wikipedia.org/wiki/Archibald…
en.wikipedia.org/wiki/Archibald…
The vast majority of bioassays are run in this dose-response format where the IC50 is a typical output. That 50% point is intuitive to grasp, and such assays are often amenable to automation and running in a high-throughput (96- or 384-well plate) format. 7/
However… an IC50 says nothing directly about the affinity of an inhibitor for its target protein. It’s just the point at which some measure of assay activity reaches 50%. 8/
Focusing in on a typical case of competitive inhibition, we’re going after ligands that compete with a natural substrate for a protein. A common example of this is an inhibitor of a kinase binding to the same site as the natural substrate, ATP. 9/
en.wikipedia.org/wiki/Protein_k…
en.wikipedia.org/wiki/Protein_k…
Intuitively, it makes sense that for such a competitive inhibitor, the IC50 is going to depend on the concentration of the natural substrate present. 10/
When the natural ligand is present in high concentration, the inhibitor has to “work harder” to compete for the binding site. Consequently, the IC50 will “right-shift” (appear less potent) at high substrate concentrations, and vice-versa. Slippery! 11/
How then to define affinity in a way that’s independent of the assay conditions? Equilibria, of course! Chemists love equilibria, so here’s a set for an enzyme, its natural substrate, and a competitive inhibitor. 12/ 

Note that because it’s a competitive inhibitor, by definition it’s an either-or for the enzyme. Either it binds the inhibitor, or the substrate. It can’t bind both simultaneously, because they bind to the same site on the enzyme. 13/
The independent measure we seek is the inhibitor dissociation constant, Ki. Ki is just the equilibrium dissociation constant for the complex between an inhibitor and its protein target. It depends only on enzyme and inhibitor. 14/ ![Ki = [E][S]/[ES]](/images/1px.png)
![Ki = [E][S]/[ES]](https://pbs.twimg.com/media/FBkziDlX0AcKik0.png)
That’s great and all, but how the hell do you *measure* a Ki? Modern biophysical methods like SPR allow one to approach this problem directly, but can we connect the dots back to those more familiar IC50s we know and love? 15/
Yeah, we can. Let’s start with the kinetic framework for enzymes. Crack open your biochemistry textbook, and you’ll find this lovely, the Michaelis-Menten equation. Sparing you the derivation - not critical for our purposes. 16/ ![Vo = Vmax*[S]/(Km+[S])](/images/1px.png)
![Vo = Vmax*[S]/(Km+[S])](https://pbs.twimg.com/media/FBkzzrLXoAoeAZt.png)
The variables are Vo = reaction velocity with no inhibitor, Vmax = maximum reaction velocity, [S] = substrate concentration, and Km (the “Michaelis constant”) = the substrate concentration at which the reaction velocity is half-maximal. 17/
(Aside: Maud Menten was a pioneer in every sense of that word. She led a pretty amazing life at a time when she had few female peers. A true OG in enzymology.) 18/
en.wikipedia.org/wiki/Maud_Ment…
en.wikipedia.org/wiki/Maud_Ment…
Sparing you another long and painful derivation, here’s what the Michaelis-Menten equation looks like factoring in the presence of an inhibitor. Here Vi is the reaction velocity in the presence of an inhibitor and [I] is the inhibitor concentration. 19/ ![Vi = Vmax*[S]/(Km(1+[I]/Ki)+[S])](/images/1px.png)
![Vi = Vmax*[S]/(Km(1+[I]/Ki)+[S])](https://pbs.twimg.com/media/FBk0GWjX0AI59Qc.png)
Now at long last we introduce our friends Cheng and Prusoff. Their insight is what will allow us to connect the dots between IC50 and Ki. They understood, for any set of conditions, at the point where [I] = IC50 that Vi = Vo / 2, so Vo = 2 * Vi. 20/ ![2*Vmax*[S]/(Km*(1+IC50/Ki)+[S]) = Vmax*[S]/(Km+[S])](/images/1px.png)
![2*Vmax*[S]/(Km*(1+IC50/Ki)+[S]) = Vmax*[S]/(Km+[S])](https://pbs.twimg.com/media/FBk0SXcXEBEYe_Z.png)
Then all you have to do is some algebra to rearrange that mess, and we arrive at our now well-known friend the Cheng-Prusoff equation. (Originally they wrote this solved for IC50, but now we often solve for Ki.) 21/ ![IC50=Ki*(1+[S]/Km)](/images/1px.png)
![IC50=Ki*(1+[S]/Km)](https://pbs.twimg.com/media/FBk0diZXoAIMlL_.png)
(Aside: William Prusoff was also a pretty remarkable guy. A CT local, he spent his career at Yale. In addition to this equation, he also gave us one of the first antiviral thymidine analogs in the 1950s… 22/
… He was also central to the discovery of stavudine (D4T, Zerit), one of the first AIDS drugs in the 1980s, later FDA-approved in 1994.) 23/
en.wikipedia.org/wiki/William_P…
en.wikipedia.org/wiki/William_P…
So now we can see clearly and mathematically that IC50 for competitive inhibitors is not a fixed number, but depends on substrate concentration [S] and the Michaelis constant Km for a given enzyme. 24/
Below is a plot of IC50 vs. [S] for an inhibitor w/ Ki = 10 nM and an enzyme w/ substrate Km = 10 uM, which are semi-typical for a garden variety kinase inhibitor and kinase. (Km is actually a little on the tight side, but it makes the plot a little cleaner.) 25/ 
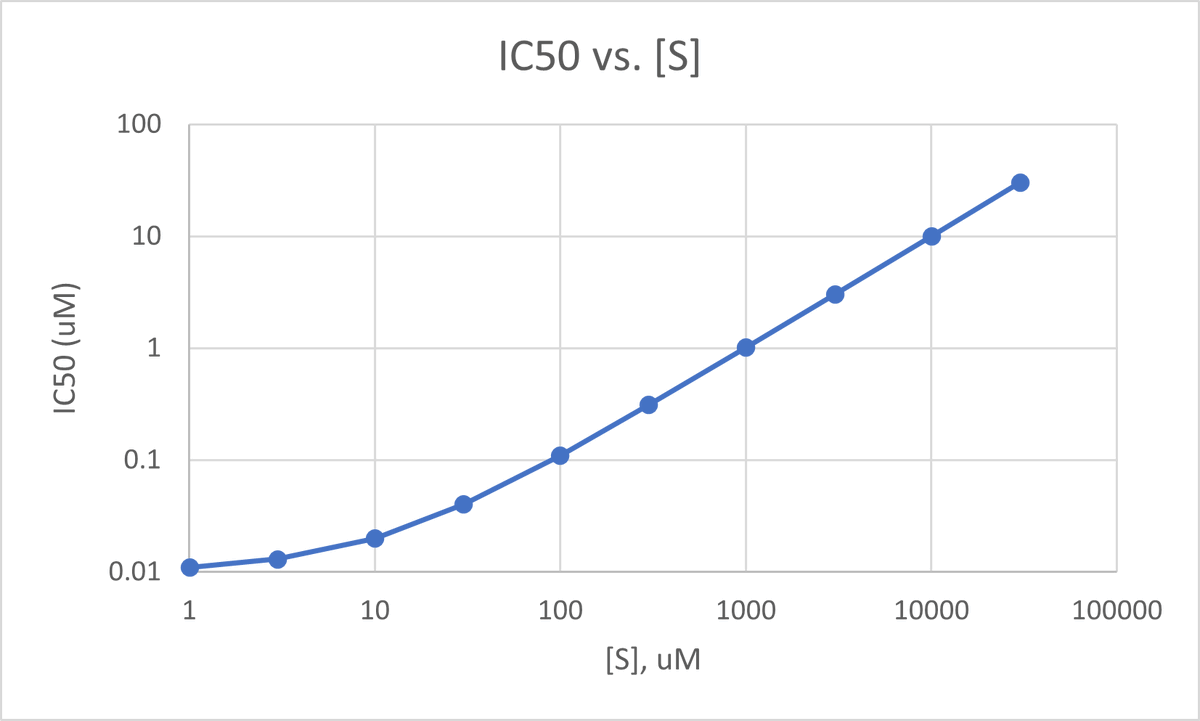
Herein lies the origin of many so-called “cell shifts” where the IC50 of an inhibitor against its target right-shifts (appears less potent) in a cellular assay vs. a biochemical one. The substrate concentrations in those two contexts may be radically different. 26/
Many biochemical assays are run at [S] = Km. Now, biochemical purists will insist this is the way to go for a host of reasons. Other folks argue for [S] = cellular substrate concentration. That’s a whole other debate that I’m not wading into. 27/
For our example kinase inhibitor, this might result in the ATP concentration being [S] = 10 uM in a biochemical assay. In a cellular environment, the ATP concentration is closer to 1 mM - 50x higher! 28/
Biophysical assays such as SPR which look at straight-up target binding are often run with no substrate present at all - and thus can give direct insight to Ki. Flip side is that they may be far removed from physiologically relevant conditions. 29/
The Cheng-Prusoff equation allows us to predict, other things being equal (which, to be fair, they rarely are), the magnitude of IC50 shift one would expect between a biochemical and a cellular assay based on differences in [S]. 30/
Now the usual pile of caveats and exceptions. 1) Michaelis-Menten kinetics assumes that the equilibria are all rapid, and therefore limited by diffusion. This isn’t always a great assumption in cells, which are slimy, viscous buckets of goo. 31/
2) It also assumes product formation is irreversible, i.e., that kcat is one-directional. This isn’t always the case. As long as [S] >> [P] though, in most cases it will appear functionally irreversible 32/
3) Tight binding kinetics creates complications when IC50 is on the same order as the enzyme concentration. This has been addressed in a more recent publication. 33/
sciencedirect.com/science/articl…
sciencedirect.com/science/articl…
4) The classical Cheng-Prusoff equation assumes competitive inhibition. In their paper, they did work through other cases of uncompetitive and noncompetitive inhibitors. But the competitive case suffices for most practical purposes. 34/
Wrapping up: IC50s are fluid, and will depend on the conditions of the assay. Ki is independent of experimental conditions, and can be estimated from an IC50 using the Cheng-Prusoff equation. 35/
When someone presents an IC50, make sure that you understand the conditions of the assay. Ask questions. Those conditions can matter very much to understanding the overall pharmacology of a compound. /end
nb - saw after posting this shift is 100x, not 50x. Need a little more coffee this morning.
Discovered another gaffe here due to my pre-coffee posting ths morning. The equation above is obviously for the substrate Kd, not the Ki. The correct equation for Ki, which features the inhibitor concentration, is here. Apologies! ![Ki=[E][I]/[EI]](/images/1px.png)
![Ki=[E][I]/[EI]](https://pbs.twimg.com/media/FBlT-TPX0AULIW1.png)
• • •
Missing some Tweet in this thread? You can try to
force a refresh







